導入
ビッグデータ時代の到来により、私たちは高次元データの処理という問題にしばしば直面します。高次元データは計算の複雑さを増大させるだけでなく、「次元の呪い」を引き起こす可能性もあります。この問題を解決するには、データの次元削減、つまり、あまり多くの情報を失わずにデータを高次元空間から低次元空間にマッピングする必要があります。主成分分析 (PCA) は、一般的に使用されるデータの次元削減方法です。
つまり、PCA の次元削減とは、最も重要な情報を保持しながら、複雑な高次元データを理解しやすい低次元データに単純化し、これらのデータをより便利に分析および処理できるようにすることです。
次の図を例にします。すべてのデータは 3 次元空間に分布しています。PCA は 3 次元データを 2 次元平面 u にマッピングします。2 次元平面はベクトル
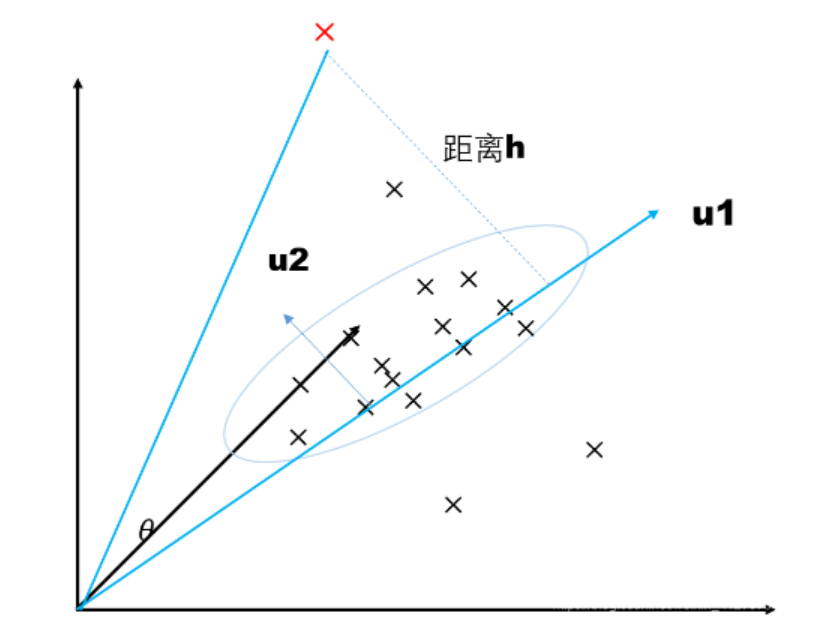
コードデモ:
import numpy as np
from sklearn.decomposition import PCA
# 创建一个包含五个数据点和两个特征的二维NumPy数组
data = np.array([[1, 1], [1, 3], [2, 3], [4, 4], [2, 4]])
# 创建一个PCA对象,通过设置 n_components 参数为 0.9,表示要保留90%的原始数据的方差
pca = PCA(n_components=0.9) # 提取90%特征
# 对输入的数据进行PCA模型拟合,计算主成分
pca.fit(data)
# 使用拟合好的PCA模型对原始数据进行转换,将数据压缩到新的特征空间,压缩后的结果存储在变量 new 中
new = pca.fit_transform(data) # 压缩后的矩阵
# 打印压缩后的数据
print("Compressed Data:")
print(new)
# 打印每个选定主成分解释的方差比例。在这里,由于指定了 n_components=0.9,它将打印每个主成分解释的方差比例,直到累积解释的方差达到90%为止
print("Explained Variance Ratios:")
print(pca.explained_variance_ratio_)
圧縮された行列:
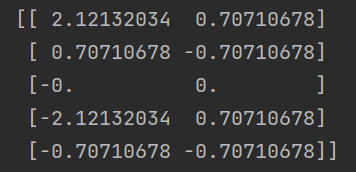
PCAによる次元削減後のデータ。この行列には、新しい特徴空間内の削減された次元のデータ ポイントの表現が含まれています。
簡単に言うと、各行は元のデータのデータ ポイントに対応し、各列は新しい主成分 (新しい特徴) に対応します。この例では、 が設定されているため、最初の主成分のみが保持されるため、新しい特徴空間の次元は 1 つだけになります。 n_components=0.9
主成分によって説明される分散の割合:
![]()
提供されたデータ セット data では、各データ ポイントに 2 つの特徴があります。次元削減に PCA を適用する場合、PCA は、最初の主成分 (最初の新しい特徴) の分散が最大で、2 番目の主成分 (2 番目の新しい特徴) の分散が 2 番目に大きい新しい特徴空間を見つけようとします。詳細な導出プロセスについては、私のブログを参照してください:PCA 次元削減の導出 (超詳細)_AI_dataloads のブログ - CSDN ブログ
このデータでは、PCA によって計算された第 1 主成分 (新しい特徴) の分散は約 0.83 ですが、第 2 主成分の分散は約 0.17 です。したがって、第 1 主成分はデータ内の変動と情報の大部分を保持しますが、第 2 主成分には比較的少ない情報が含まれます。したがって、次元削減後は、第 1 主成分のみが保持され、第 2 主成分の情報は破棄されます。
これが、次元削減後に主成分が 1 つだけ残る理由、つまり[0.83333333, 0.16666667]です。これは、次元削減されたデータセットには主成分が 1 つだけ含まれており、最初の主成分の寄与が支配的である一方、2 番目の主成分の寄与は比較的小さいため除去されることを意味します。これが PCA の仕組みであり、データ内の最も重要な変更をキャプチャし、次元を削減して冗長性を削減しようとします。