デュアルサポートベクターマシン
P6 2.1

L1 では線形サポート ベクター マシンについて説明し、次に L2 ではデュアル サポート ベクター マシンについて説明します。

前のセクションでは、非線形 SVM を見つける方法について説明しました。z 空間に変換する場合、QP 問題を解くには d ~ + 1 個の変数 (および N 個の定数) が必要です。解くには、d ~は非常に大きく、場合によっては無限になります。 SVM は d ~に依存しない:

元の SVM を等価な SVM に変換できます。

これは二重問題です:

前の正則化に従い、λ を導入し、条件付き問題を無条件問題に変換でき、λ の個体は数値は N


でラグランジュ関数を定義します。関連文献では通常、λ を α と書き

、SVM を正しい式に変換します。st

の (b,w) が満たされない場合、1-yn(wTzn+b) は整数になります。 max が選択されている場合、最終的に min になるため、無限大に達します。これにより、st を満たさない (b,w) が除外されます。それが満たされる場合、yn(
wTzn+b) は非になります。 -負の数。最大値と >=0 があるため、yn(wTzn+b)=0 ( ∑ \sumであることに注意してください)∑、a>=0 であるため、各項目が 0 に等しい場合にのみ合計が 0 に等しくなります)、その場合、式は1 2 w T w \frac{1}{2} w^Tw21wT w。
このようにして、st を満たさないデータを効果的に排除し、最小の1 2 w T w \frac{1}{2} w^Tw を21wてか。_
P7 2.2
の前のセクションでは、SVM をラグランジュの公式に変換しましたが、その公式の下限をどのように見つけるか? 任意の (b,w) について、次のことが当てはまります。

これは任意の場合に当てはまるため、最大の右辺の式を取ることも依然として当てはまります。

これが解決されると、右辺の式はラグランジュ双対 (双対) 問題になります。問題は、SVM の下限を見つけることです。

緑の 3 つの条件が満たされているため、(QP 問題に対して) 強い関係があり、直接等式化できます。また、方程式の両側を満たすグループ (b、w、α) が存在することも示しています。 : 今は制限がないので、

これを解き始めます:
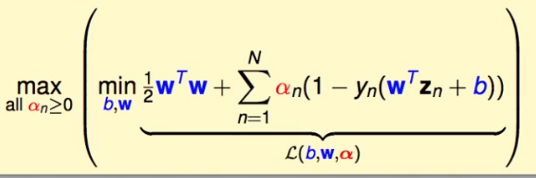
これは min なので、要件:
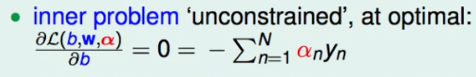
したがって、この制限を追加して式を簡素化できます:

最後の項目は b*0 であることがわかり、次のようになります:

同様に、min があるため、L に w = 0 の偏導関数を求め、w を固定数にしてから単純化を開始する必要があります。max の後に次の一連の規則があるため、Min は無視できます。式には b と w は含まれておらず、残りは α だけを考慮する必要があります。

最後に、最適化を満たす 4 つの条件は KKT です。追加: 4 番目の点 (ハリー ポッターとヴォルデモートは 1 つ生きていなければなりません)、yn(wTzn+b)=1 (点はちょうど境界線上にあり、これらの α>=0 点は SV です) の場合、式は自然です。は 0, >1 です。2.1 の最後の図によると、2.1 の図の式には min がかかり、αn は 0 しか取れません。したがって、ここでの最終的な式も 0 になります。

②L(b,w,α) の定義に戻ると、yn と zn=1、そして w= ∑ α nynzn \ であることがわかります。sumα_ny_nz_n∑あるんyんzんそれが出てきました。③sigma の各項目は 0 (KKT の下) でなければならないので = 0 になるからです。 α2(w-3) の問題については、具体的な w、yn、zn の作り方は無視して大丈夫な気がします。つまり、全体が0になるはずです。
P8 2.3
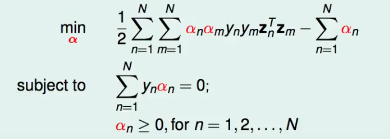
前のセクションの式を max->min に単純化し、それを 2 乗します。w = ... を加えない条件は、クロスフォーカスが αn にあるためです。次に、これが凸 (凸) QP 問題であることがわかりました。N 個の変数 (αn) があり、N+1 条件 (制約) (N αn はゼロより大きくなければなりません、1 ∑ n = 1 N yn α n = 0) \ sum_{n=1}^N y_nα_n=0∑n = 1Nyんあるん=0、合計 N+1)、QP の設定を開始します。

注: 通常、QP を入力するときは、「=」を 2 つの不等式に分割する必要はありません。直接記述してから範囲境界を直接記述します。

ただし、q は密な密な行列、つまり、その中の多くの値が非ゼロではなく、計算量と保存量が大きいため、SVM 用に特別に設計された方法が使用されることに注意してください。

KKT の 4 つの条件を通じて、w と b を導入できます。特に、α n > 0 α_n > 0あるん>0 ,1 − yn ∗ ( w T zn + b ) = 1 1-y_n*(w^Tz_n+b) = 11−yん∗( wツズん+b )=1、および =1 は、その点が SVM のファット境界 (ファット境界) 上にあることを意味します。その理由は次のとおりです。。超平面をもう一度見る必要があると推定されています。

P9 2.4

前のセクションで α > 0 がわかっている場合、その点は境界上にあります。ただし、分類線上の点は必ずしもサポート ベクトルであるとは限りません (α = 0 の可能性もあります)。そのため、α>0 の点をサポート ベクトル (SV) と呼び、これらの SV (つまり、α>0) のみをサポート ベクトル (SV) と呼びます。範囲が少し絞られるかもしれません。

したがって、w と b はどちらも SV でなければ、つまり α = 0 の場合には意味がありませんので、SV のみで計算することができます。
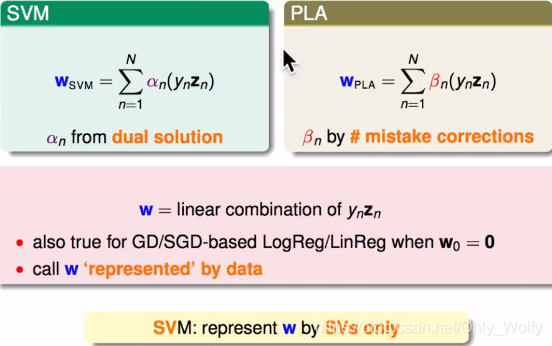
SVM と PLA の式は非常に似ており、両方ともynzn y_nz_nです。yんzん他の w の線形結合も同様であり、w がデータで表されていると言えます。SVM の w は SV のみで表され、PLA はエラーが発生したポイントで表されます。哲学的には、私たちは「w」を表現するために何を使うべきかを知る必要があります。

SVM の 2 つの表現 (プライマルとデュアル) を比較すると、ハード マージンは、ooxx の厳密な分類では間違いが発生しないことを意味します。通常はデュアル SVM が使用されます。

最後に:dual svm は N に関係するだけだと言われていますが、実際には q の中に d ~が隠されています。次に、この d ~を回避する方法を説明します。
最終的なまとめ:
