目次
- ストリーミングネットワーク
- 残留ネットワーク
- パスを増強する
- フローネットワークの切断
- Ford-Fulkerson方法
- コード
文章
この記事では主に最大流量問題のフォード・フルカーソン解法について説明します。実行時間の異なる複数の実装が含まれているため、これはアルゴリズムではなくメソッドであると言えます。この方法は、残差ネットワーク、拡張パス、カットという 3 つの重要なアイデアに基づいています。
3つの概念を紹介する前に、フォード・フルカーソン法の基本的な考え方を簡単に紹介しましょう。最初に理解すべきことは、Ford-Fulkerson が反復手法であるということです。初めに、すべての u, v は V に属し、f(u, v)=0 (f(u, v) は u から v へのエッジの現在のフローを表します)、つまりフローの値です。初期状態では0です。各反復で、「増加パス」を見つけることによってフロー値を増やすことができます。オーグメンテーション パスは、ソース s からシンク t までのパスとして見ることができ、それに沿ってより多くのフローを押してフローの値を増やすことができます。このプロセスは、すべての増強パスが見つかるまで、つまり最大のネットワーク フローが得られるまで繰り返されます。
図に示すように、各線は拡張されたパスを表し、s から t への電流の流れは 3 であることを例に挙げます。
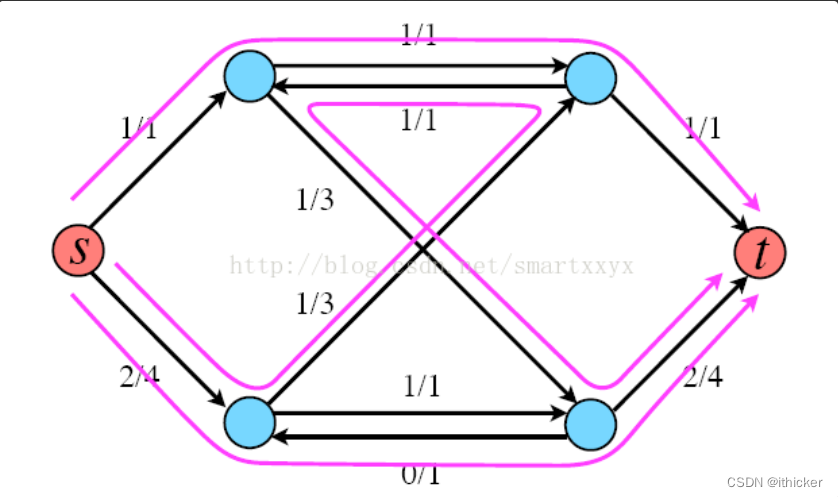
もちろん、これはネットワークの最大フローではありません。拡張パスを見つけるためのアルゴリズムに従って、実際に拡張パスの検索を続けることができます。最終的な最大フロー ネットワークは次の図に示されており、最大フローは 4 です。 。
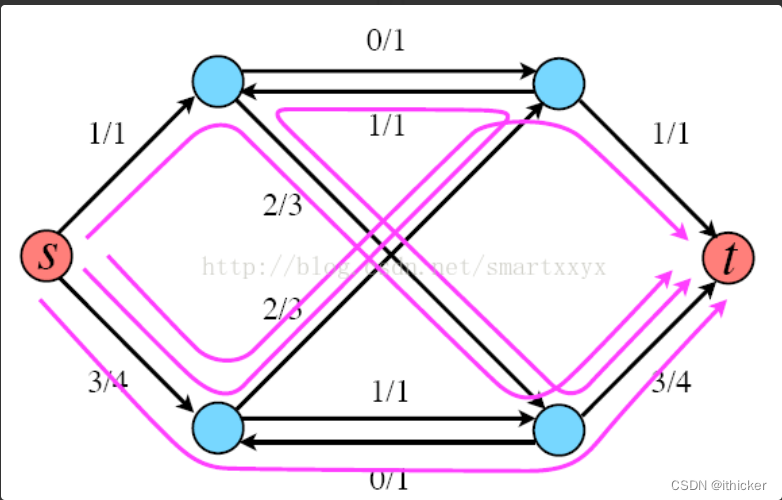
次に、拡張パスを見つける方法を紹介します。拡張パスを導入する前に、まず残差ネットワークの概念を導入する必要があります。
ストリーミングネットワーク
まずストリーミング ネットワークの定義を見てみましょう。フロー ネットワークについては、「アルゴリズム入門」の第 26 章で次のように定義されています。
フロー ネットワーク G = (V, E) は有向グラフであり、グラフ内の各エッジ (u, v) ∈ E は非負の容量値 c(u, v) >=0 を持ちます。また、エッジ集合 E にエッジ (u, v) が含まれる場合、グラフ内に反対側のエッジ (v, u) は存在しません。(u, v) ∉ E の場合、便宜上 c(u, v) = 0 と定義します。また、グラフ内では自己ループは許可されません。フロー ネットワーク内のすべてのノードの中で、特に 2 つの特別なノード、つまりソース ノード s とシンク ノード t を区別します。
この定義を例を挙げて説明しましょう。以下の有向グラフを見てください。図中、sはソースノード(source)、tはシンクポイント(sink)である。つまり、頂点 s については、頂点 s から始まるエッジのみが存在でき、t については、頂点 s で終了するエッジのみが存在できます。図の各辺の上にある数字は、この辺の容量値 c です。たとえば、c(s, v) = 6。グラフにはエッジ (s, z) がないため、 c(s, z) = 0 になります。グラフには自己ループ エッジ、つまり(s, s) のようなエッジは存在できません。2 点間の実際の流量値を f(u, v) で表します。



残留ネットワーク

名前が示すように、残留ネットワークとは、特定のネットワークと、まだ収容可能なフローに対応するフローで構成されるネットワークを指します。具体的には、ネットワーク G = (V, E)、そのソース ポイント s、シンク ポイント t と仮定します。f を頂点 u から頂点 v への流れに対応する G 内の流れとします。C(u, v) (C はエッジ容量を表します) を超えない条件下で、u から v にプッシュできる追加のネットワーク トラフィックは、エッジ (u, v) の残りの容量 (残余容量) です。は次のように定義されます。
r(u,v)=c(u,v)-f(u,v)
たとえば、(u, v) の現在のトラフィックが 3/4 であると仮定すると、c(u, v)=4、f(u, v)=3、r(u, v)=1 となります。
ネットワークの流れにはそのような法則があることがわかっています。u から v へのフローの 3 単位がすでに存在するため、反対方向から見ると、v から u への 3 単位の残差ネットワークが存在し、r(v, u)=3 となります。このように、u から v への 3 つの単位フローがあり、v から u へはこれら 3 つの単位フローを押し戻す能力があることが理解できます。
例を詳しく見てみましょう。下の図に示すように、フロー ネットワーク
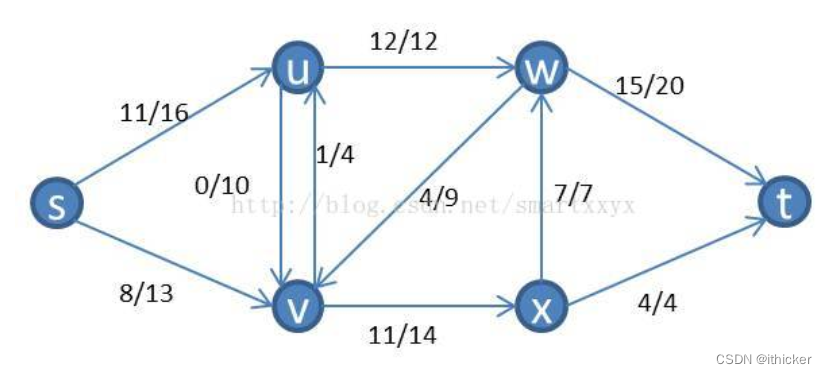
とそれに対応する残差ネットワークは次のとおりです。
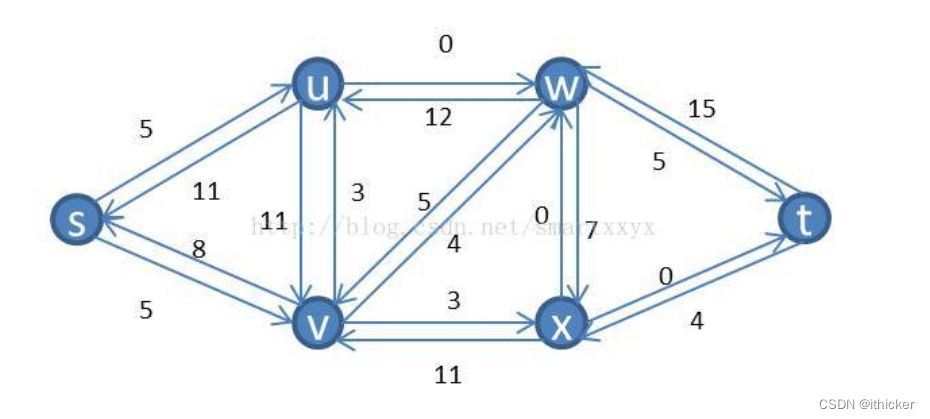
パスを増強する
残差ネットワークを理解した後、拡張パスを導入しましょう。フロー ネットワーク G とフロー f が与えられると、** 拡張パス p は、その残差ネットワーク Gf 内の s から t への単純なパスです。**視覚的に理解すると、エッジ キャパシティを侵害しない s から t へのパスが存在することがわかります。このパスにトラフィックをプッシュすると、ネットワーク全体のフロー値が増加する可能性があります。上記の残余ネットワークには、このような拡張パスがあります。つまり、
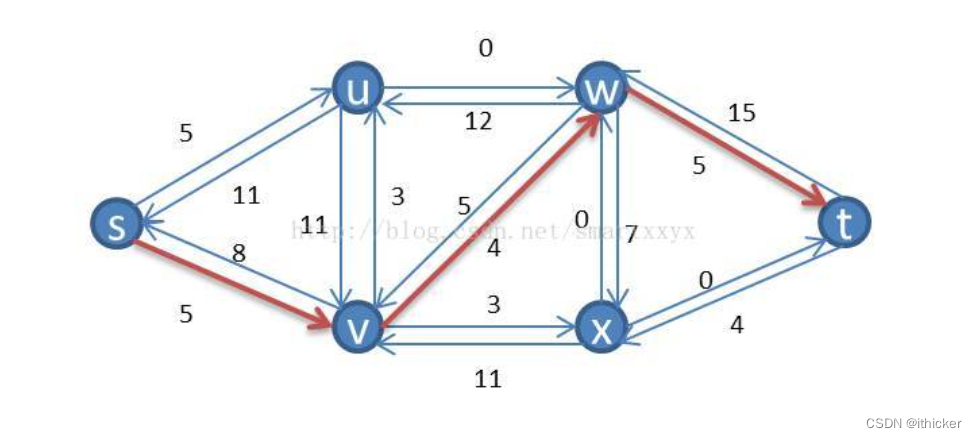
4 ユニットのフローをプッシュでき、プッシュ後、元のフロー ネットワークよりも 4 つのフローが多い新しいフロー ネットワークが得られます。現時点では、見つからなくなるまで、同じ方法を使用して新しいフロー ネットワーク上の拡張パスを見つけ続けます。この時点で、最大のネットワーク フローが得られます。
フローネットワークの切断
上記は方法の紹介に過ぎませんが、拡張経路が見つからない場合、現在のネットワークが最大流量ネットワークであることをどのように証明するのでしょうか? これには、最大流量最小カット定理の使用が必要です。
まず、カットの概念をご紹介します。フロー ネットワーク G(V, E) のカット (S, T) は、V を S と T=VS の 2 つの部分に分割するため、s は S に属し、t は T に属します。切断能力(S、T)は、セット S からセット T までのすべてのエッジ(方向付き)の能力の合計を指します(反対方向はカウントしません。S-àT でなければなりません)。f がフローの場合、cut(S,T) を通る正味フローはf(S,T) として定義されます (S → T の正の値、T→S の負の値を含む)。引き続き上記の例を取り上げ、次の図に示すようにランダムなカットを描画します。
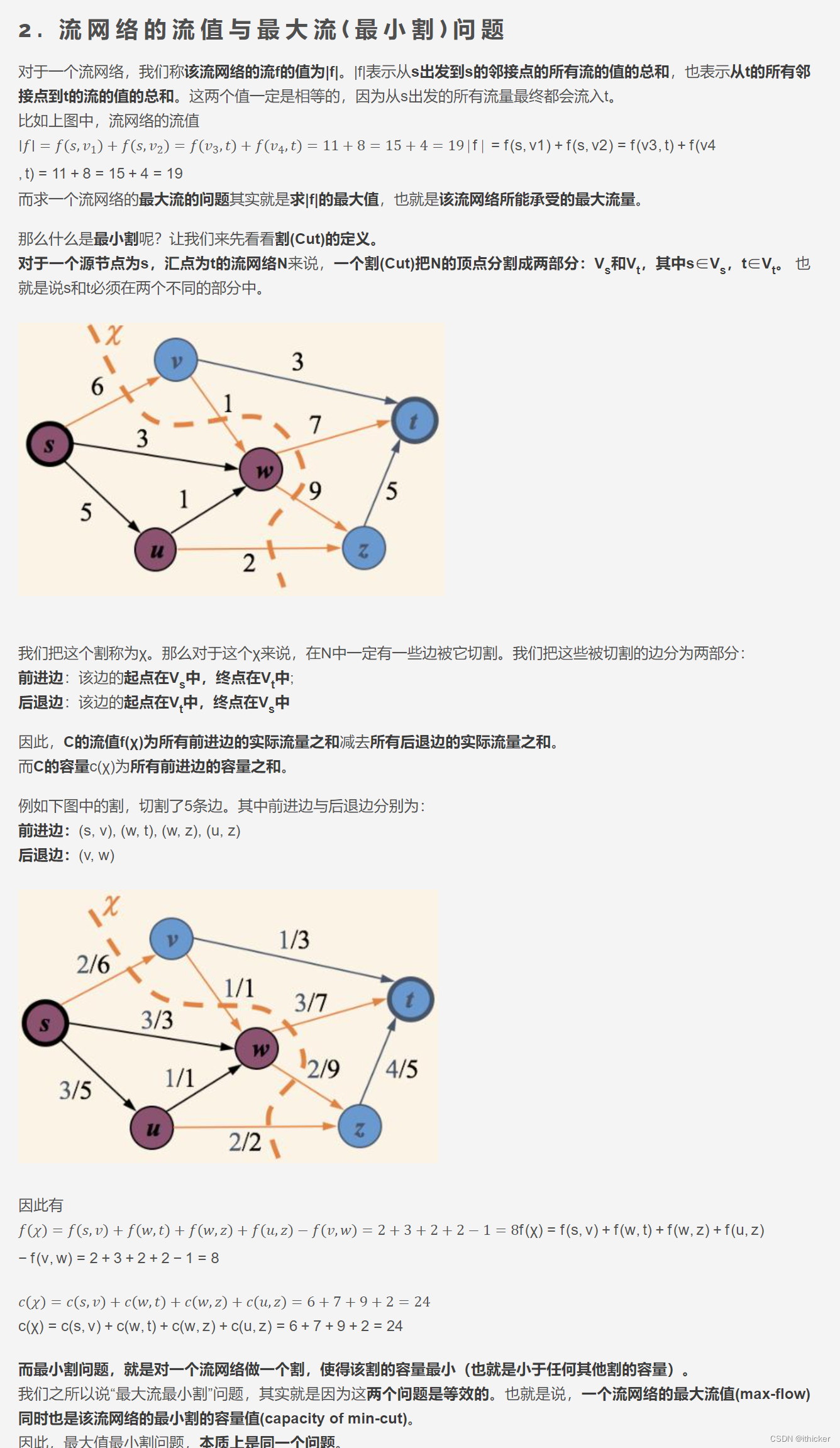
明らかに、どのようなカットでも、カットを通過する正味の流量の上限はカットの容量であり、カットの容量を超えることは不可能です。したがって、ネットワークの最大フローはネットワークの最小カットを超えてはなりません。最小カットは最小のカット容量を指し、最大流量はネットワーク内の最大の正味流量を指します。簡単な例としては、蛇口が継続的に水を排出することが挙げられます。これらの側面はパイプに相当し、各パイプの容量では対応できません。実際には、それは実用的なカットで表されます. 最小カットは、パイプラインシステム全体で見つかる最も狭いポイント、つまり、パイプラインの特定のセクションの最小流量とすべての水の総量ですある段階を通過する水の流れを流量で表します 最大流量 ある段階でパイプラインを通過する水の最大量であり、この最大流量を超えるとパイプラインの能力を超えます。したがって、s から t まで水の流れを確保したい場合は、水の流量、つまり最大流量が以下になるようにする必要があります。ただし、水をできるだけ早く流すためには、最大流量を最小カットと同じにする必要があるため、最適化のプロセスで最大流量を見つけることは、最小カットを見つけることと同じです。 2 つは本質的に同じ問題です。
しかし、これは残りのネットワーク上のパスの増強とどのような関係があるのでしょうか?
まず特徴を理解する必要があります. 前回の記事で述べた最大流量問題の線形計画表現によれば, 流れネットワークの流れ保存の原理が述べられています. この原理によれば, 任意のカットがネットワークの正味のフローはすべて等しいです。具体的な証明は難しくありません。下の図でグラフで理解できます。上の

カットと比較して、集合 S 内の u と v が少なく、ソース点 s から集合 T への正味の流れは u に流れます。一方、前のカット グラフでは、集合 S から集合 T へのフローは、u および v から集合 T への正味のフローと等しくなります。このうち、w も u と v に流れますが、この部分の流れはパスがないためソース点 s に流れることができません。そのため、この部分の流れは s から u と v への流れを追加し、流れはu と v の間は何があっても相互に転送され、最終的に集合 T に流れるため、このフロー値は u と v に流れる s の値に等しくなります。s を蛇口にたとえると、u や v から他の場所に流れる水はすべて s から来ており、それ自体で水の流れを作り出すことは不可能です。したがって、どのカットの正味流量も等しく、カットの正味流量が流量です。最大値が得られると、それは最大流量となり、最小カットと等しくなります。これが流量保存の性質であり、どこにいても流れは平等です。
Ford-Fulkerson 法 (FORD-FULKERSON アルゴリズムで最大流量と最小カットを計算)
Ford-Fulkerson アルゴリズムを見てみましょう。このアルゴリズムでは貪欲な戦略も使用されます。まずアルゴリズムの擬似コードを見てください。

疑似コードは次のように理解されます。


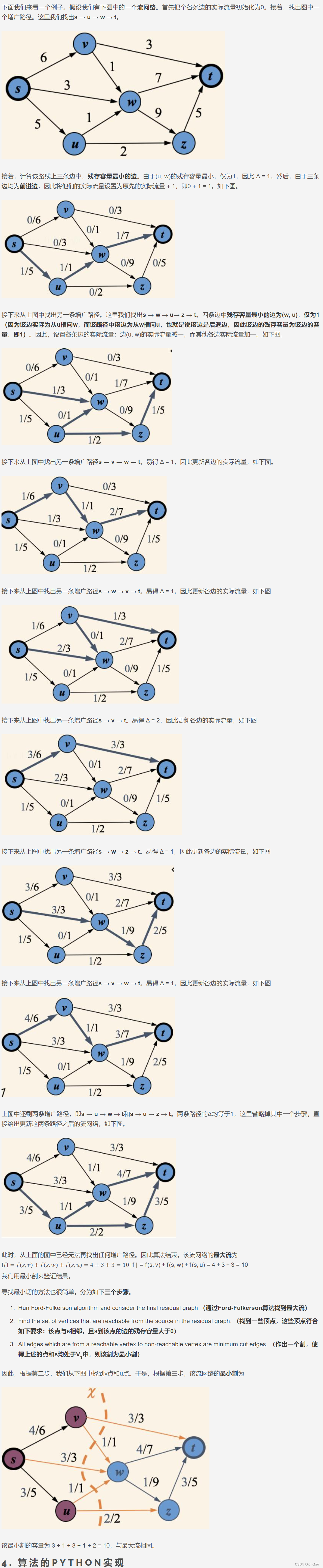
参考
https://www.freesion.com/article/67541250323/
https://www.cnblogs.com/DarrenChan/p/9563511.html