1. アルゴリズム分析

アルゴリズムの研究の最終的な目標は、同じ要件を満たすためにどのように時間とメモリを占有するかを削減することであり、異なるアルゴリズム間の時間消費とスペース消費の違いをケースを通じて実証することであることは以前に紹介しました.占有される時間とスペースなので、次に、アルゴリズムの時間消費とアルゴリズムのスペース消費の説明と分析について学びます。アルゴリズムの時間消費の分析は、アルゴリズムの時間複雑度分析と呼ばれ、アルゴリズムのスペース消費分析は、アルゴリズムのスペース複雑度分析と呼ばれます。

1.1 アルゴリズムの時間計算量分析

アルゴリズムの消費時間を計算したいのですが、まずアルゴリズムの実行時間を測定する必要があります。

事後分析推定方法：

より簡単に考えるには、アルゴリズムを数回実行し、タイマーを使用して時間を計ります. このイベント後の統計の方法は非常によく見えます, 実際に電卓を使用する必要はありません.コンピュータ側で計算するため、両方ともタイミング機能を提供します。この統計的方法は、主にコンピュータータイマーを使用して、設計されたテストプログラムとテストデータを通じて異なるアルゴリズムでコンパイルされたプログラムの実行時間を比較し、アルゴリズムの効率を判断しますが、この方法には大きな欠点があります。アルゴリズムに基づいてコンパイルされたテストプログラムを実現しますが、これには通常多くの時間とエネルギーがかかります. テストが終わった後、テストが非常に悪いアルゴリズムであることが判明した場合、それまでの作業はすべて無駄になります.テスト環境（ハードウェア環境）の違いテスト結果の違いも大きく異なります。

public static void main(String[] args) {
    
    
	long start = System.currentTimeMillis();
	int sum = 0;
	int n=100;
	for (int i = 1; i <= n; i++) {
    
    
		sum += i;
	}
	System.out.println("sum=" + sum);
	long end = System.currentTimeMillis();
	System.out.println(end-start);
}

事前分析と見積もり方法:
コンピュータープログラムを作成する前に、統計的方法に従ってアルゴリズムを見積もります. 要約すると、高級言語で作成されたプログラムがコンピューター上で実行されるのにかかる時間は、次の要因:

アルゴリズムによって採用された戦略と解決策。
コンパイルによって生成されたコードの品質。
問題の入力スケール (いわゆる問題入力スケールは入力の量です)。
マシンが命令を実行する速度。

コンピューターのハードウェアとソフトウェアに関連するこれらの要因に関係なく、プログラムの実行時間はアルゴリズムの品質と問題の入力スケールに依存することがわかります。

アルゴリズムが固定されている場合、アルゴリズムの実行時間は問題の入力サイズにのみ関係します。
分析の例として、前の合計のケースを取り上げてみましょう。

要件:
1 から 100 までの合計を計算します。
最初の解決策:

//如果输入量为n为1，则需要计算1次；
//如果输入量n为1亿，则需要计算1亿次；
public static void main(String[] args) {
    
    
	int sum = 0;//执行1次
	int n=100;//执行1次
	for (int i = 1; i <= n; i++) {
    
    //执行了n+1次
		sum += i;//执行了n次
	}
	System.out.println("sum=" + sum);
}

2番目の解決策:

//如果输入量为n为1，则需要计算1次；
//如果输入量n为1亿，则需要计算1次；
public static void main(String[] args) {
    
    
	int sum = 0;//执行1次
	int n=100;//执行1次
	sum = (n+1)*n/2;//执行1次
	System.out.println("sum="+sum);
}

したがって、入力サイズが n の場合、1 つ目のアルゴリズムは 1+1+(n+1)+n=2n+3 回実行され、2 つ目のアルゴリズムは 1+1+1=3 回実行されます。最初のアルゴリズムのループ本体を全体と見なし、終了条件の判断を無視すると、2 つのアルゴリズムの実行時間の差は、実際には n と 1 の差になります。

Algorithm 1 でループ判定が n+1 回実行され、数が多いように見えますが、無視できるのはなぜですか? 次の例を見てみましょう。

要件: 100 1+100 2+100 3+...100 100コード
の結果を計算します。

public static void main(String[] args) {
    
    
	int sum=0;
	int n=100;
	for (int i = 1; i <=n ; i++) {
    
    
		for (int j = 1; j <=n ; j++) {
    
    
			sum+=i;
		}
	}
	System.out.println("sum="+sum);
}

上記の例では、ループの条件が何回実行されるかを正確に調べたい場合、非常に面倒なことであり、実際に和を計算するコードは内側のループのループ本体であるため、アルゴリズムの効率、分析を簡素化するコアコードの実行時間のみを考慮します。

アルゴリズムの複雑さを研究し、何回実行する必要があるかを正確に特定するのではなく、入力スケールが増加し続けた場合のアルゴリズムの成長の抽象化 (法則) に焦点を当てます。長期的な最適化などの再コンパイルの問題を考慮する必要があり、1 次と 2 次に陥りやすいです。

プログラムの作成に使用する言語や、これらのプログラムが実行されるコンピューターの種類は気にしません。実装するアルゴリズムだけを気にします。このように、ループインデックスのインクリメントやループ終了の条件、変数の宣言、結果の出力などに関係なく、プログラムの実行時間を分析する際に最も重要なことは、プログラムをアルゴリズムまたはアルゴリズムとして見なすことです。プログラミング言語に依存しない一連のアルゴリズム。アルゴリズムの実行時間を分析するとき、最も重要なことは、コア操作の数を入力スケールに関連付けることです。

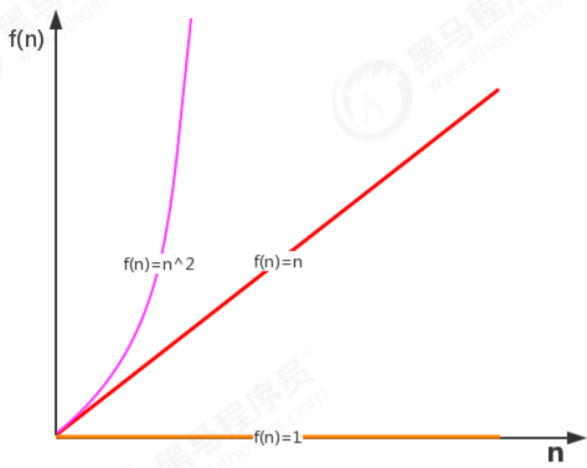
ここに画像の説明を挿入

1.1.1 関数の漸近的成長

概念
2 つの関数 f(n) と g(n) が与えられた場合、すべての n>N に対して f(n) が常に g(n) より大きくなるような整数 N が存在する場合、f(n) は漸近的に速く成長すると言います。 g(n) よりも。

概念が少しわかりにくいので、次にいくつかテストしてみましょう。

テスト 1:
4 つのアルゴリズムの入力サイズがすべて n であると仮定します。

アルゴリズム A1 は 2n+3 操作を実行する必要があります。これは、次のように理解できます。最初に n サイクルを実行し、実行が完了した後、さらに n サイクルがあり、最後に 3 つの操作があります。
アルゴリズム A2 には 2n 回の操作が必要です。
アルゴリズム B1 は 3n+1 操作を実行する必要があります。これは次のように理解できます: 最初に n ループを実行し、次に n ループを実行し、次に n ループを実行し、最後に 1 つの操作を行います。
アルゴリズム B2 には 3n 回の操作が必要です。

では、上記のアルゴリズムのどれがより高速ですか?
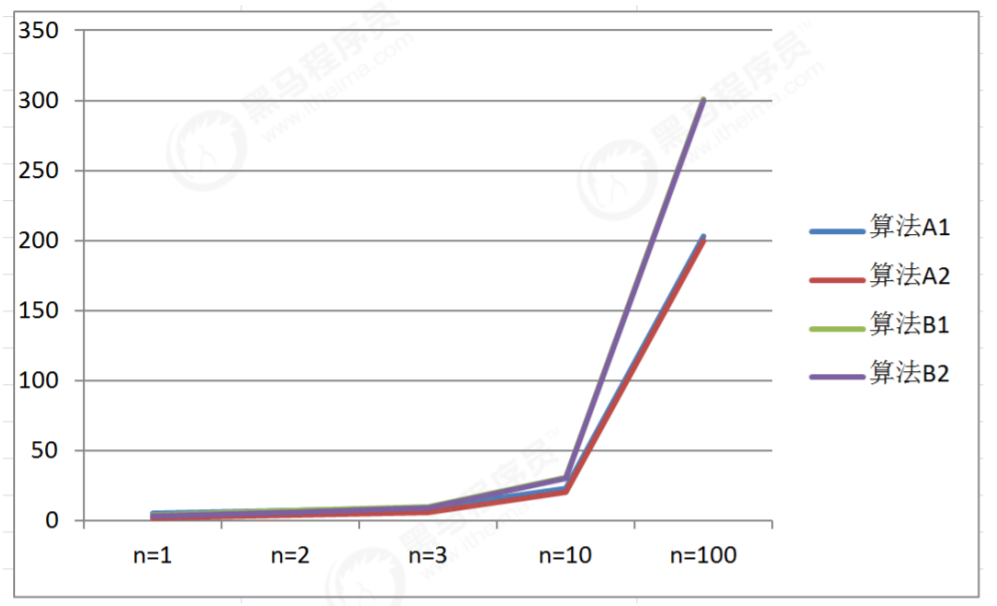
ここに画像の説明を挿入

データテーブルから、アルゴリズム A1 とアルゴリズム B1 を比較します:
入力スケール n=1 の場合、A1 を 5 回実行する必要があり、B1 を 4 回実行する必要があるため、A1 の効率は B1 の効率よりも低くなります
。入力スケール n=2, A1 は 7 回実行する必要があり、B1 は 7 回実行する必要があるため、A1 の効率は B1 と同じです; 入力サイズ n>2 の場合、実行
回数A1 が必要とする実行回数は、B1 が必要とする実行回数よりも常に少ないため、A1 の効率は B1 の効率よりも高くなります。

したがって、次のように結論付けることができます。

入力規模が n>2 のとき、アルゴリズム A1 の漸近成長はアルゴリズム B1 よりも小さい.
折れ線グラフを観察すると、入力規模が大きくなるにつれて、アルゴリズム A1 とアルゴリズム A2 が徐々に重なり合い、アルゴリズム B1とアルゴリズム B1 は徐々に重なり、アルゴリズム B2 は徐々に重なり合って 1 つになるため、
入力サイズが大きくなるにつれて、アルゴリズムの定数演算は無視できると結論付けられます。

テスト 2:
4 つのアルゴリズムの入力サイズがすべて n であると仮定します。

アルゴリズム C1 は 4n+8 操作を行う必要があります
アルゴリズム C2 は n 操作を実行する必要があります
アルゴリズム D1 は 2n^2 操作を実行する必要があります
アルゴリズム D2 は n^2 操作を実行する必要があります

では、上記のアルゴリズムのどれがより高速ですか?
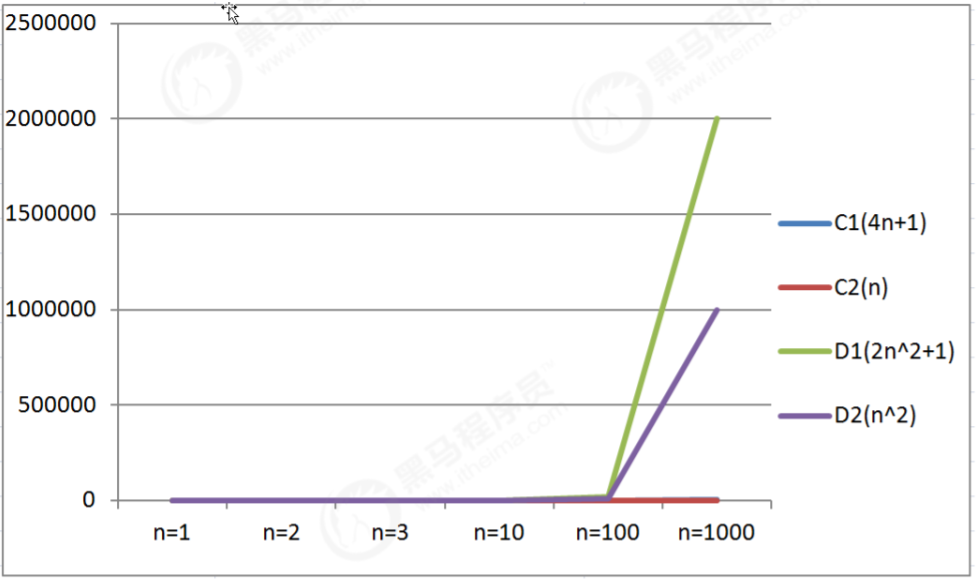
ここに画像の説明を挿入

データテーブルを通じて、アルゴリズム C1 とアルゴリズム D1 を比較します。
入力スケール n<=3 の場合、アルゴリズム C1 の実行時間はアルゴリズム D1 の実行時間よりも長くなるため、アルゴリズム C1 の効率は低くなります。入力スケール n> の場合
。図３に示すように、アルゴリズムＣ１の実行時間はアルゴリズムＤ１よりも短く、したがってアルゴリズムＤ２は効率が低く、
一般にアルゴリズムＣ１はアルゴリズムＤ１よりも優れている。

折れ線グラフを使用して、アルゴリズム C1 と C2 を比較対照します。

入力サイズが大きくなるにつれて、アルゴリズム C1 とアルゴリズム C2 がほぼオーバーラップします。

折れ線グラフを通して、アルゴリズム C シリーズとアルゴリズム D シリーズを比較します。
入力スケールが増加するにつれて、n^2 の前の定数要素が削除されても、D シリーズの回数は D シリーズの回数よりもはるかに多くなります。 Cシリーズ。

したがって、入力サイズが大きくなるにつれて、定数に最高次の項を掛けた値は無視できると結論付けることができます。

テスト 3:
4 つのアルゴリズムの入力スケールが n であるとします:
アルゴリズム E1: 2n^2+3n+1;
アルゴリズム E2: n^2
アルゴリズム F1: 2n^3+3n+1
アルゴリズム F2: n^3
次に、上記アルゴリズム、どちらが速いですか?

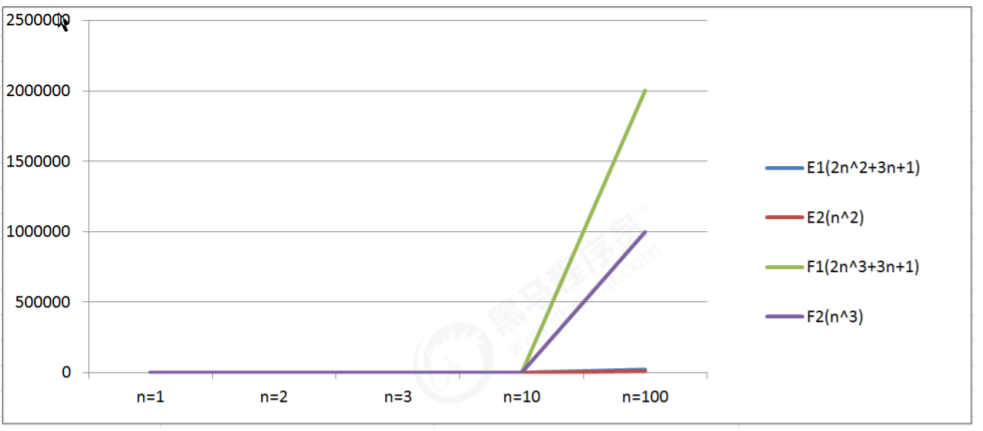
ここに画像の説明を挿入

データテーブルを通じて、アルゴリズム E1 とアルゴリズム F1 を比較します:
n=1 の場合、アルゴリズム E1 とアルゴリズム F1 の実行回数は同じです; n
>1 の場合、アルゴリズム E1 の実行回数は、アルゴリズムの実行回数よりもはるかに少なくなります。アルゴリズム F1 の実行;
したがって、アルゴリズム E1 全体として、アルゴリズム F1 によるものです。

折れ線グラフから、アルゴリズム F シリーズは n の増加に伴い特殊になり、アルゴリズム E シリーズはアルゴリズムFに比べて n の増加に伴い遅くなることがわかります。アイテムのインデックスが大きく、n が大きくなると、結果も非常に速く大きくなります

テスト 4:
5 つのアルゴリズムの入力サイズが n であると仮定します:
アルゴリズム G: n^3;
アルゴリズム H: n^2;
アルゴリズム I: n
アルゴリズム J: logn
アルゴリズム K: 1

では、上記のアルゴリズムのどれがより効率的でしょうか?
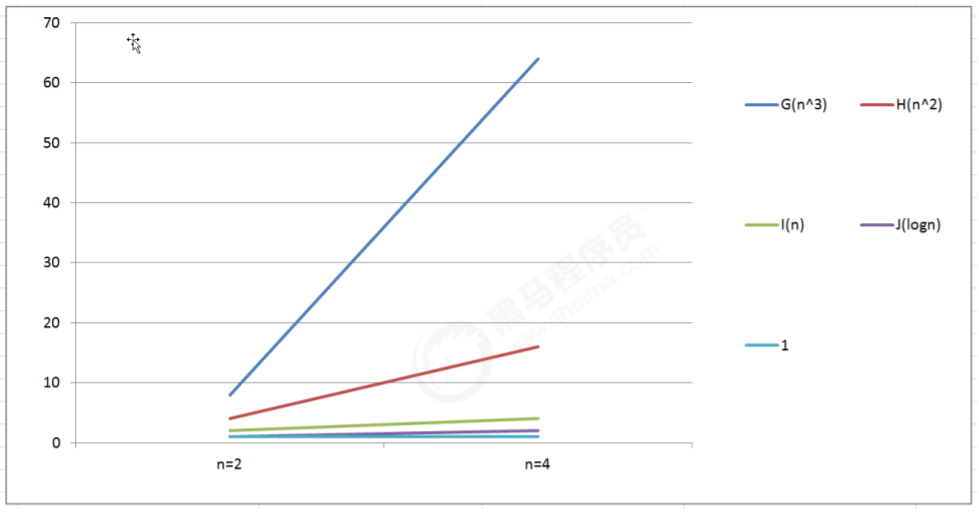
ここに画像の説明を挿入

データテーブルと折れ線グラフを観察することにより、結論を導き出すのは簡単です。
アルゴリズム関数の n の最高べき乗が小さいほど、アルゴリズムの効率が高くなります。

要約すると、アルゴリズムの成長を入力スケールと比較すると、次のルールに従うことができます。

アルゴリズム関数の定数は無視できます。
アルゴリズム関数の最大累乗の定数係数は無視できます。
アルゴリズム関数の最大電力が小さいほど、アルゴリズム効率が高くなります。

1.1.2 アルゴリズム時間の複雑さ

1.1.2.1 Big O表記

意味

アルゴリズムを分析する場合、ステートメントの合計実行時間 T(n) は問題サイズ n の関数であり、n による T(n) の変動を分析し、T(n) の大きさを決定します。アルゴリズムの時間計算量は、T(n)=O(f(n)) として表されるアルゴリズムの時間尺度です。これは、問題のサイズ n が増加するにつれて、アルゴリズムの実行時間の増加率が f(n) の増加率と同じであることを意味します。これは、アルゴリズムの漸近時間複雑度、または略して時間複雑度と呼ばれます。ここで、f (n) は問題サイズ n の関数です。

ここで、1 つのことを明確にする必要があります: 実行回数 = 実行時間.
大文字の O() を使用して、アルゴリズムの時間の複雑さの表記法を反映させます。一般に、入力サイズ n が大きくなると、T(n) の成長が最も遅いアルゴリズムが最適なアルゴリズムになります。

以下では、ビッグ O 表記を使用して、一部の加算アルゴリズムの時間計算量を表現しています。

アルゴリズム 1

public static void main(String[] args) {
    
    
	int sum = 0;//执行1次
	int n=100;//执行1次
	sum = (n+1)*n/2;//执行1次
	System.out.println("sum="+sum);
}

アルゴリズム 2

public static void main(String[] args) {
    
    
	int sum = 0;//执行1次
	int n=100;//执行1次
	for (int i = 1; i <= n; i++) {
    
    
		sum += i;//执行了n次
	}
	System.out.println("sum=" + sum);
}

アルゴリズム 3

public static void main(String[] args) {
    
    
	int sum=0;//执行1次
	int n=100;//执行1次
	for (int i = 1; i <=n ; i++) {
    
    
		for (int j = 1; j <=n ; j++) {
    
    
			sum+=i;//执行n^2次
		}
	}
	System.out.println("sum="+sum);
}

判定条件の実行時間と出力ステートメントの実行時間を無視すると、入力サイズが n の場合、上記のアルゴリズムの実行時間は、アルゴリズム 1: 3 回アルゴリズム 2: n+3
回
アルゴリズム
3 : n^2+2 二流

上記の各アルゴリズムの時間計算量をビッグオー表記で表すとしたら、どのように表現すればよいでしょうか? 関数の漸近成長の分析に基づいて、次のルールを使用してビッグ O オーダーの表現を導き出すことができます。

実行時のすべての追加定数を定数 1 に置き換えます。
変更された実行回数では、高次項のみが保持されます。
最高次の項が存在し、定数係数が 1 でない場合は、この項を掛けた定数を削除します。

したがって、上記のアルゴリズムのビッグ O 表記は次のとおりです。
アルゴリズム 1: O(1)
アルゴリズム 2: O(n)
アルゴリズム 3: O(n^2)

1.1.2.2 一般的な Big-O オーダー

1. 線形順序には
、通常、線形順序を含むネストされていないループが含まれます. 線形順序とは、入力スケールが拡大するにつれて、対応する計算数が線形に増加することを意味します. たとえば:

public static void main(String[] args) {
    
    
	int sum = 0;
	int n=100;
	for (int i = 1; i <= n; i++) {
    
    
		sum += i;
	}
	System.out.println("sum=" + sum);
}

上記のコードの場合、ループ本体のコードを n 回実行する必要があるため、ループの時間計算量は O(n) です。

2. 正方次数
一般的なネストされたループは、この時間複雑度に属します。

public static void main(String[] args) {
    
    
	int sum=0,n=100;
	for (int i = 1; i <=n ; i++) {
    
    
		for (int j = 1; j <=n ; j++) {
    
    
			sum+=i;
		}
	}
	System.out.println(sum);
}

上記のコードでは、n=100、つまり、外側のループが実行されるたびに、内側のループが 100 回実行されます. プログラムがこれら 2 つのループから抜け出したい場合は、100*100 回実行する必要があります。 . これは n の 2 乗なので、このコードの時間計算量は O(n^2) です。

3. 3 次順序
一般に、3 レベルのネストされたループは、この時間計算量に属します。

public static void main(String[] args) {
    
    
	int x=0,n=100;
	for (int i = 1; i <=n ; i++) {
    
    
		for (int j = i; j <=n ; j++) {
    
    
			for (int j = i; j <=n ; j++) {
    
    
				x++;
			}
		}
	}
	System.out.println(x);
}

上記のコードでは、n=100、つまり、外側のループが実行されるたびに、中央のループが 100 回実行され、中央のループが実行されるたびに、最も内側のループが 100 回実行される必要があります。 3 つのループのうち、n の 3 乗である 100100100 回実行する必要があるため、このコードの時間計算量は O(n^3) です。

4. 対数の順序
対数は高校数学の内容であり、当解析プログラムは主にプログラムに基づいており、数学で補完されていますので、あまり心配する必要はありません。

int i=1,n=100;
while(i<n){
    
    
	i = i*2;
}

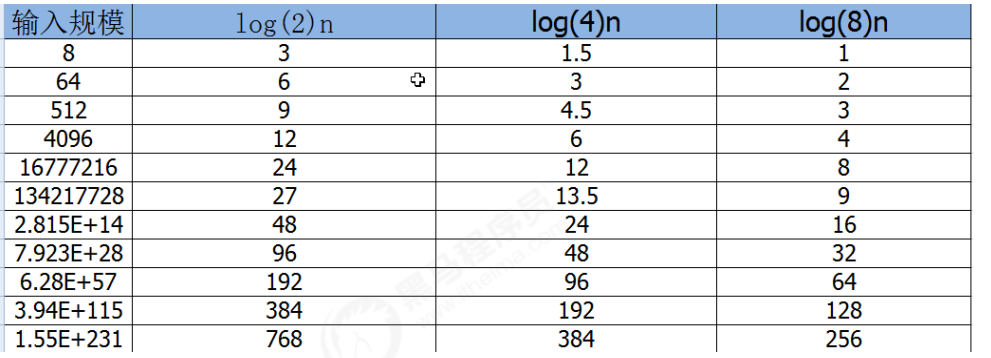
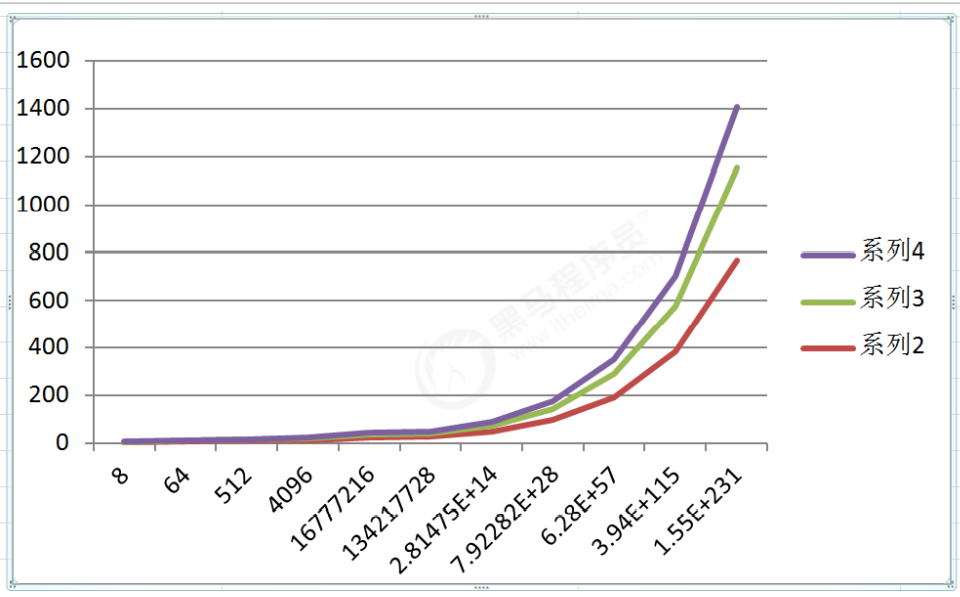
i*2 を超えるたびに、n に 1 ステップずつ近づくため、n より大きくなるように乗算された x 2 があると仮定すると、ループは終了します。2^x=n なので x=log(2)n となり、このサイクルの時間計算量は O(logn) となります。

対数次数の場合、入力スケール n が大きくなるにつれて、底が何であっても増加傾向は同じであるため、底を無視します。

ここに画像の説明を挿入

5. 一定次数
一般に、ループ操作を伴わないものは一定次数です。これは、n が大きくなっても操作の数が増えないためです。例えば：

public static void main(String[] args) {
    
    
	int n=100;
	int i=n+2;
	System.out.println(i);
}

上記のコードは、入力サイズ n に関係なく 2 回実行されます. Big O 導出規則によれば、定数は 1 に置き換えられるため、上記のコードの時間計算量は O(1) です。

一般的な時間の複雑さの概要を次に示します。

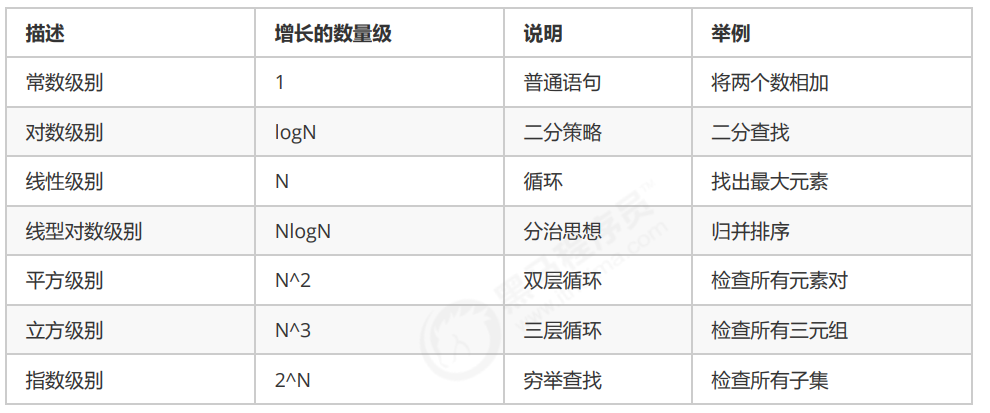
ここに画像の説明を挿入
それらの複雑さは、低いものから高いものまで次のとおりです。

 O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)

前の折れ線グラフの分析によると、平方オーダーから始めて、入力スケールが増加するにつれて時間コストが急激に増加することがわかります. したがって、アルゴリズムは O(1), O( logn), O(n) を追求します、O(nlogn) これらの種類の時間の複雑さ、およびアルゴリズムの時間の複雑さが2乗オーダー、3次オーダー、またはそれ以上の複雑であることが判明した場合、このアルゴリズムを分割することはお勧めできません。最適化する必要があります。

1.1.2.3 関数呼び出しの時間計算量分析

前に、単一の関数でアルゴリズムコードの時間計算量を分析し、次に関数呼び出し中の時間計算量を分析しました。

ケース番号1：

public static void main(String[] args) {
    
    
	int n=100;
	for (int i = 0; i < n; i++) {
    
    
		show(i);
	}
}

private static void show(int i) {
    
    
	System.out.println(i);
}

main メソッドには for ループがあり、ループ本体は show メソッドを呼び出します. show メソッド内で実行されるコードは 1 行だけなので、show メソッドの時間計算量は O(1) であり、時間計算量はメインメソッドのO(n)

ケース 2:

public static void main(String[] args) {
    
    
	int n=100;
	for (int i = 0; i < n; i++) {
    
    
		show(i);
	}
}

private static void show(int i) {
    
    
	for (int j = 0; j < i; i++) {
    
    
		System.out.println(i);
	}
}

main メソッドには for ループがあり、ループ本体は show メソッドを呼び出します. show メソッド内にも for ループがあるため、show メソッドの時間計算量は O(n) です。主な方法は O(n ^2) です

ケース 3:

public static void main(String[] args) {
    
    
	int n=100;
	show(n);
	for (int i = 0; i < n; i++) {
    
    
		show(i);
	}
	for (int i = 0; i < n; i++) {
    
    
		for (int j = 0; j < n; j++) {
    
    
			System.out.println(j);
		}
	}
}

private static void show(int i) {
    
    
	for (int j = 0; j < i; i++) {
    
    
		System.out.println(i);
	}
}

show メソッドでは for ループがあるため、show メソッドの時間計算量は O(n) であり、main メソッドでは、コード show(n) の行の内部実行回数は n であり、最初のfor ループは show メソッドを呼び出すため、その実行時間はですn^2。ネストされた 2 番目の for ループでは 1 行のコードのみが実行されるため、その実行時間はですn^2。この場合、メインメソッドの合計実行時間はですn+n^2+n^2=2n^2+n。ビッグ O 導出規則に従って、n を削除して最上位項目を保持し、最上位項目の定数係数 2 を削除するため、メインメソッドの最終的な時間計算量は O(n^2) です。

1.1.2.4 最悪の場合

心理学的な観点からは、誰もが何が起こるかについて期待を持っています. たとえば、半分の水を見たとき、誰かが言うでしょう: わあ、まだ半分の水があります! しかし、一部の人々はこう言うでしょう：神よ、水はコップ半分しかありません。多くの人は、将来の失敗を心配し、最悪の事態を想定して計画を立てる傾向があるため、最悪の結果が生じた場合でも、当事者は心理的に準備ができており、結果を受け入れやすくなっています。最悪の結果が来なければ、当事者はとても幸せになるでしょう。

アルゴリズム解析も同様で、必要があれば
n個の乱数を格納した配列があれば、そこから指定された数を見つけてください。

public int search(int num){
    
    
	int[] arr={
    
    11,10,8,9,7,22,23,0};
	for (int i = 0; i < arr.length; i++) {
    
    
		if (num==arr[i]){
    
    
			return i;
	    }
	}
	return -1;
}

最良のケース:
最初に調べた数値が予想される数値であり、アルゴリズムの時間計算量は O(1) です。

最悪の場合:
最後の数値が期待される数値であり、アルゴリズムの時間計算量は O(n) です。

平均的なケース:
数値ルックアップの平均コストは O(n/2) です

最悪の場合を保証といいます.本アプリにおいて最も基本的な保証であり,最悪の場合でも正常にサービスを提供することができます.したがって,特に断りのない限り,ここでいう実行時間は最悪の場合の実行時間を指します.

1.2 アルゴリズムの空間複雑度分析

コンピュータのハードウェアとソフトウェアは、特にコンピューティングの環境を提供するメモリとして、比較的長い進化の歴史を経験しており、初期の 512k から、1M、2M、4M... と、現在の 8G、さらには 16G までを経験しました。および 32G であるため、初期の頃は、動作中のアルゴリズムのメモリ使用量も考慮しなければならないことが多い問題でした。アルゴリズムのスペースの複雑さを使用して、アルゴリズムのメモリ使用量を説明できます。

1.2.1 Java での一般的なメモリ使用量

1. 基本的なデータ型のメモリ使用量:
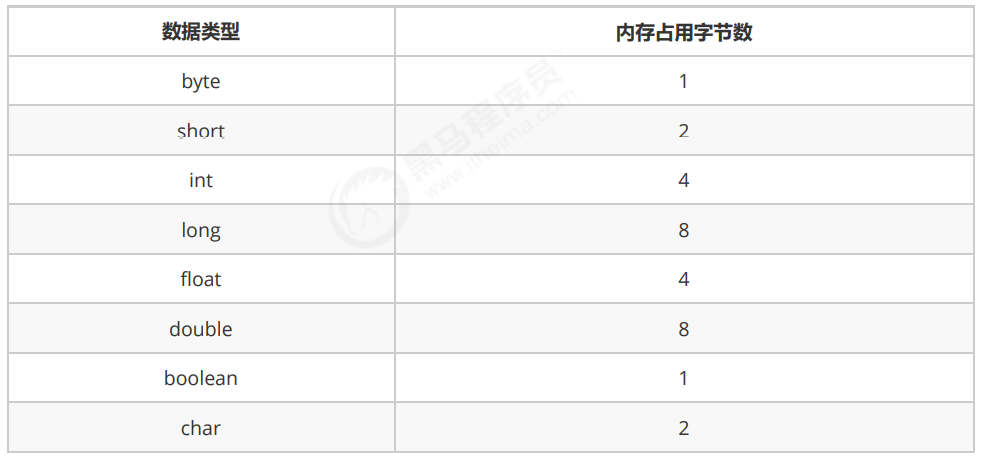
ここに画像の説明を挿入

2. コンピュータがメモリにアクセスする方法は、一度に 1 バイトです。
ここに画像の説明を挿入
3. 参照 (マシンアドレス) を表すには 8 バイトが必要です。
たとえば、Date date = new Date() の場合、変数 date は表すために 8 バイトを占める必要があります。

4. new Date() などのオブジェクトを作成します. Date オブジェクト内に格納されたデータ (年、月、日など) によって占有されるメモリに加えて、オブジェクト自体にもメモリのオーバーヘッドがあります. オーバーヘッド各オブジェクトの長さは 16 バイトで、オブジェクトのヘッダー情報を保存するために使用されます。

ここに画像の説明を挿入
5. 一般メモリの使用。8 バイト未満の場合、自動的に8 バイトに埋められます。type s の配列には通常、24 バイトのヘッダー情報 (独自のオブジェクトの 16 オーバーヘッド、長さの 4 バイト、および 4 のパディングバイト) と、値を保持するために必要なメモリが必要です。

1.2.2 アルゴリズムの空間複雑度

Java のメモリの最も基本的なメカニズムを理解すると、多数のプログラムのメモリ使用量を効果的に見積もることができます。
アルゴリズムのスペースの複雑さの計算式は次のように記録されます。 nによって。

ケース:
指定された配列要素を反転し、反転した内容を返します。
解決策 1:

public static int[] reverse1(int[] arr){
    
    
	int n=arr.length;//申请4个字节
	int temp;//申请4个字节
	for(int start=0,end=n-1;start<=end;start++,end--){
    
    
		temp=arr[start];
		arr[start]=arr[end];
		arr[end]=temp;
	}
	return arr;
}

解決策 2:

public static int[] reverse2(int[] arr){
    
    
	int n=arr.length;//申请4个字节
	int[] temp=new int[n];//申请n*4个字节+数组自身头信息开销24个字节
	for (int i = n-1; i >=0; i--) {
    
    
		temp[n-1-i]=arr[i];
	}
	return temp;
}

判定条件が占有するメモリを無視すると、メモリ使用量は次のようになります。

アルゴリズム 1:
着信配列のサイズに関係なく、常に追加の 4+4=8 バイトを適用します。

アルゴリズム 2:
4+4n+24=4n+28;

ビッグ O 導出規則によると、アルゴリズム 1 の空間複雑度は O(1)、アルゴリズム 2 の空間複雑度は O(n) であるため、空間占有の観点からは、アルゴリズム 1 はアルゴリズム 2 よりも優れています。

Javaにはメモリガベージコレクションメカニズムがあり、jvmもプログラムのメモリ使用量を最適化します（ジャストインタイムコンパイルなど）ため、Javaプログラムのメモリ使用量を正確に評価することはできませんが、基本的なメモリ使用量を知っている. java を使用すると、次のことができます。 Java プログラムのメモリ使用量を推定します。

現在のコンピュータ機器のメモリは一般的に比較的大きいため、基本的にパーソナルコンピュータは 8G から始まり、大型のものは 32/64G に達する可能性があるため、メモリ使用量は通常、アルゴリズムのボトルネックではありません.複雑さ.デフォルトはアルゴリズムの時間複雑度です.

ただし、実行しているプログラムが組み込み開発である場合、特に一部のセンサーデバイスの組み込みプログラムの場合、これらのデバイスのメモリは非常に小さく、通常は数 kb であるため、アルゴリズムのスペースの複雑さに対する要件があります。今回ですが、一般的にJava開発を行う方は基本的にサーバー開発であり、一般的にはそのような問題はありません。

データ構造とアルゴリズム II アルゴリズム解析