ICLR 2023
1 イントロ
- 時系列は通常、連続的に記録され、各時点で記録されるスカラー量はわずかです
- 以前の多くの研究では、時間的な依存関係を把握するために時間次元の変化を調べてきました
- —>連続性、傾向、周期性など、時系列の多くの固有の特性を反映および抽出できます。
- ただし、リアルタイムの時系列データの時系列は通常、非常に複雑な時間の特徴で構成されており、さまざまな時間次元の変化が混在するため、時間次元の変化をモデル化することは非常に困難です。
- 以前の多くの研究では、時間的な依存関係を把握するために時間次元の変化を調べてきました
- 深層学習の分野では、多くのモデルが非線形性をモデル化する強力な機能を備えているため、複雑な時間次元の変化を時系列で捉えることができます。しかし、それぞれにいくつかの欠点があります
- RNN: マルコフ仮定 (時間 t-1 での観測が時間 t での予測に影響する) に基づいて、連続モーメントの時系列特性をモデル化します。
- このような方法では、長期的な時間依存性をモデル化するのが難しいことがよくあります
- 同時に、並列化できないので効率が心配
- TCN: 時間次元での畳み込みニューラル ネットワークの使用
- 時系列の 1 次元の隣接関係により、TCN は時間次元の同様の時点での時系列機能のみをモデル化できます。
- --> 長期的な時間の依存関係をモデル化することはまだできません
- 変圧器、自己注意
- 各離散時系列観測値の前に内積関係のみを使用すると、実際の相互依存関係が得られるとは限りません。
- RNN: マルコフ仮定 (時間 t-1 での観測が時間 t での予測に影響する) に基づいて、連続モーメントの時系列特性をモデル化します。
- この論文では、複数期間の観点から時系列を観察します
- 時系列はしばしば複数の期間を示します
- たとえば、気象データには、日周期と年周期があります。
- 電力消費データには、週ごとのサイクルと四半期ごとのサイクルがある場合があります
- 各期間の各瞬間における時系列の観測値は、隣接する地域の時間特性の影響を受けるだけでなく、隣接する期間の対応する位置の時間特性によっても決定されます。
- 論文では、intraperiod-variation(サイクル内の変化)、interperiod-variation(サイクル間の変化)と呼ばれています。
- サイクル内変動は、サイクル内の短期的な一時的特性を表します
- 周期的変動は、期間間の長期的な時間的特性を表します
- 時系列に周期性がない場合、その周期は無限であると見なすことができ、その時間特性はその周期内の変化によってのみ決定されます
- 時系列はしばしば複数の期間を示します
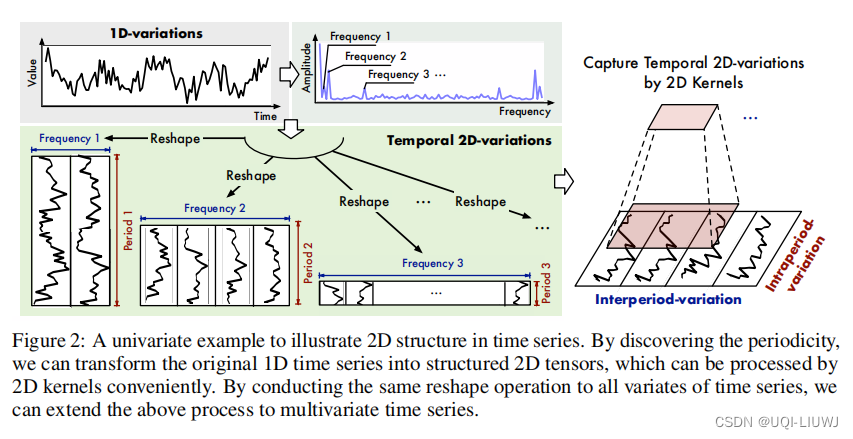
- 1 次元の時系列が 2 つの異なる時間次元の変化を明示的に表現することは困難です
- ->この論文は、1 次元の時系列を一連の 2 次元テンソルに再形成します。ここで、各テンソルの列はサイクルを表し、行は異なるサイクルの同じ対応する位置 (同じフェーズ) を表します。
- この再形成後、サイクル内およびサイクル間の時間依存性を適切にモデル化できます
- 各列の隣接する要素は、隣接する時系列の前の時間依存性を表し、各行の隣接する要素は、異なる期間の同じフェーズの前の時間依存性を表します
-

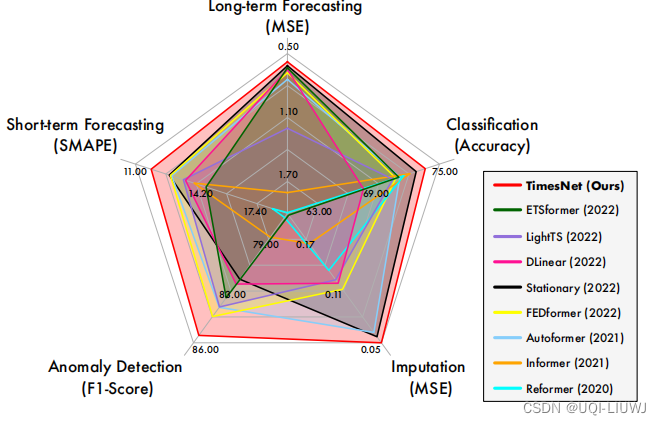
- 上記の 1 次元時系列から 2 次元テンソルへの変更に基づいて、著者は TimesNet を提案しました. 実験により、長期/短期時系列予測、時系列補完、時系列分類、および時系列異常検出タスク. パフォーマンス
- 同時に、TimesNet は複数期間の時系列機能を考慮して分離し、時系列をより適切に特徴付けることができます。
2タイムズネット
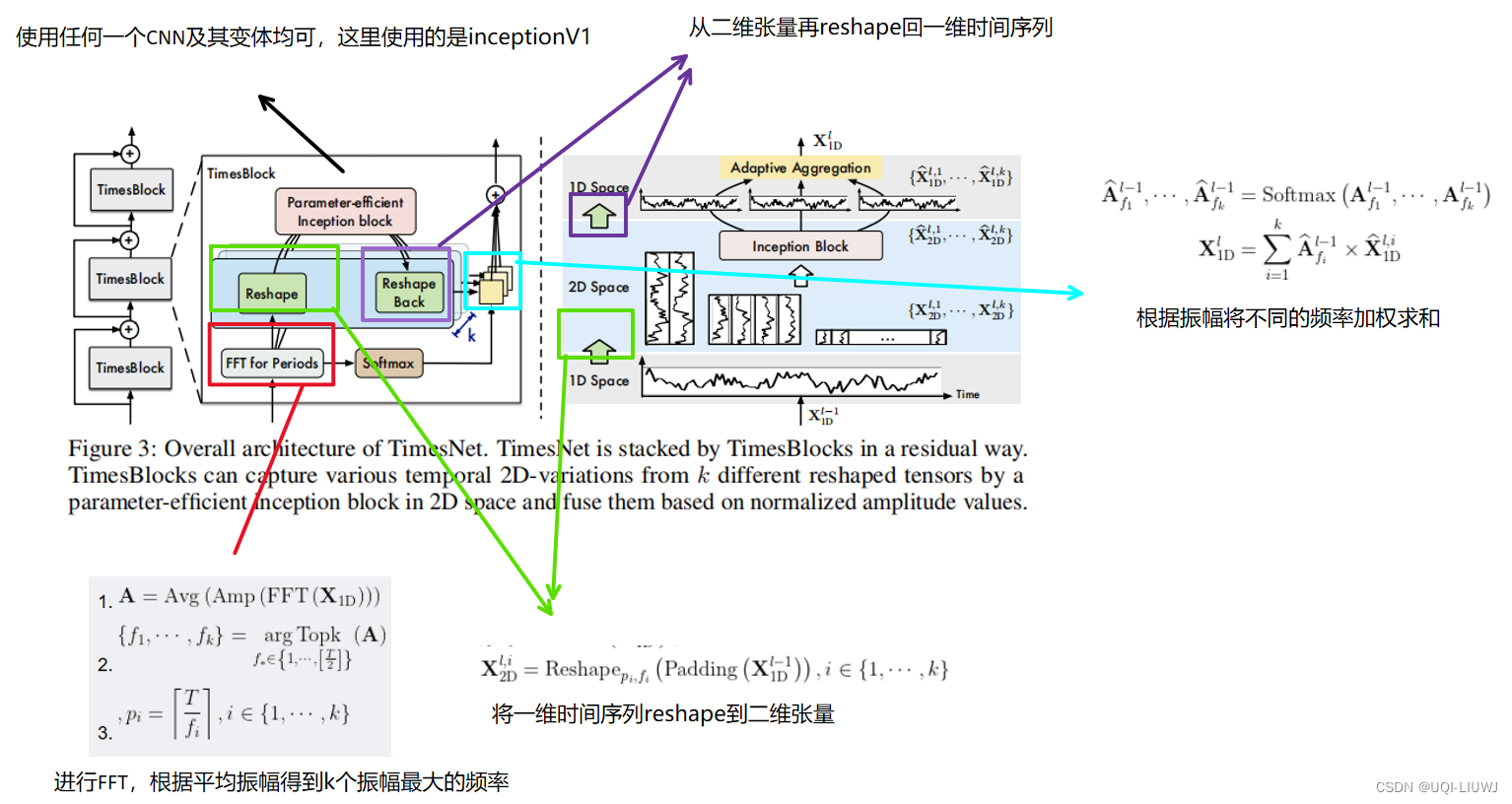
2.1 一次元時系列から二次元テンソルへの変換
次の 3 つの式で表すことができます。
- 式1
- FFT(.) は、1 次元時系列の高速フーリエ変換を表します (個人的な理解では、N の長さの時間領域信号を N/2 の長さのスペクトル領域信号に変換することです)。
- Amp は、各時系列変換後の各周波数での振幅です。
- Avg は、異なる時系列の振幅の平均です
- —> A は異なる周波数の平均振幅です
- フォーミュラ 2
- 平均振幅が最大の k 個の周波数を取る
- 式3
- 対応する k サイクルを取得する
- 考察を容易にするために、論文では上記の 3 つの式を次のように簡略化しています。
に基づいて、1 次元時系列を
一連の 2 次元テンソルに変換できます
。ここで、i 番目の 2 次元テンソル
は次のように計算されます。
- ここでのパディングの役割は、時系列の最後に 0 を追加して、2 次元テンソルに再形成できるようにすることです。
2.2 タイムズブロック
- ここでは残りの接続が使用されます
- 入力用
- 最初の層は、
埋め込み層を直接供給することによって得られます
- 各レイヤーの後、入力は で
、出力は
- 入力用
2.2.1 2D 時間次元の変化のキャプチャ
- 最初の行: 前の TimesBlock の出力によると、対応する平均振幅、最大振幅を持つ k 個の周波数、および対応する周期が取得されます。
- 2 行目は、これらの k 周波数に従って、1 次元時系列を異なる 2 次元テンソルに再形成します。
- 3 行目、ここに inception v1 の 機械学習ノートがあります: inceptionV1 inceptionV2_machine learning inception_UQI-LIUWJ のブログ - CSDN ブログもちろん、他の CNN 派生モデルも利用できます。
- 4 行目で、最初に学習した 2 次元表現を1 次元時系列に
再形成します。
- Trunc を使用して、時系列の長さを元の T にスケーリングします。
2.2.2 適応加算
- 前のステップで が得られたので、
それらをどのように組み合わせるのですか?
- 最初の行で取得した平均振幅に従って、softmax を実行して対応する重みを取得し、k 個のアイテムを重み付けして合計します。
3回の実験
3.1 データセット
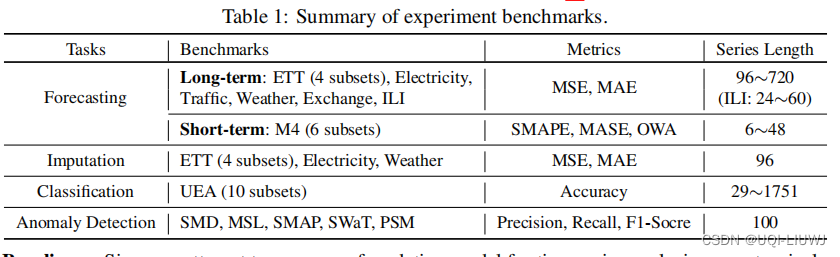
この論文では、長期時系列予測、短期時系列予測、時系列補完、時系列分類、異常検出の 5 つの問題を比較しています。

3.2 主な結果
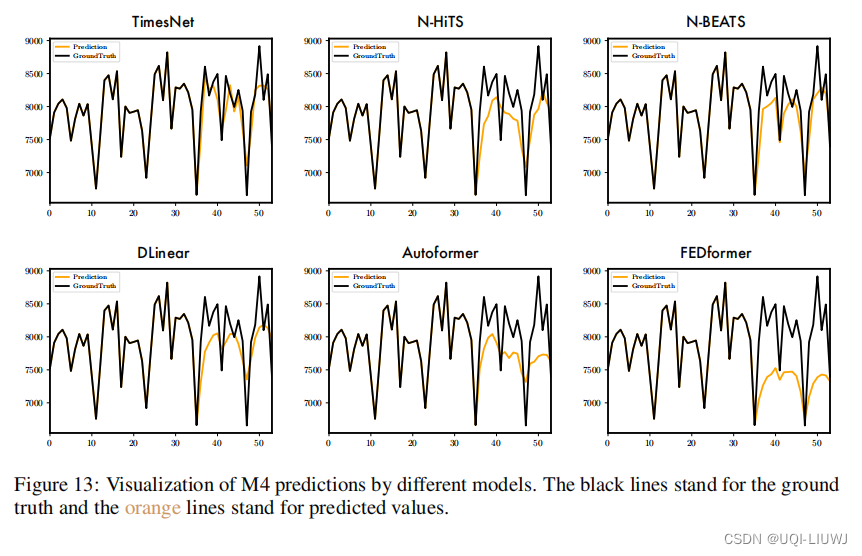
3.2.1 短期時系列予測

3.2.2 長期時系列予測

3.2.3 時系列の完成

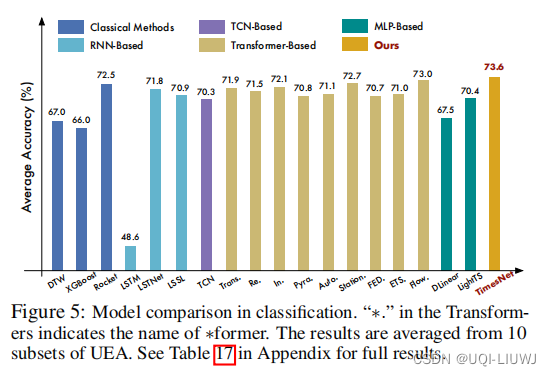
3.2.4 時系列分類
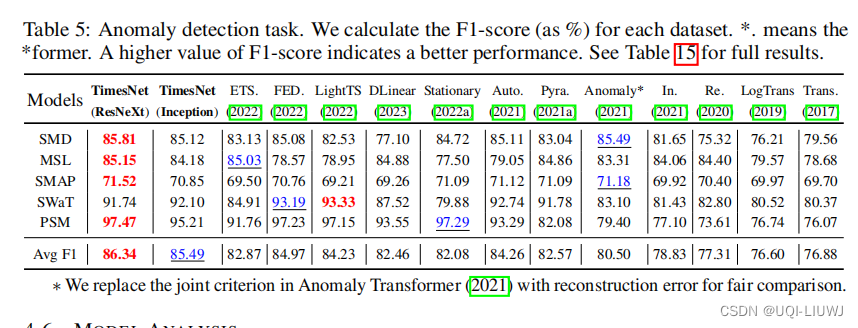
3.2.5 時系列異常検出
3.3 2D 時系列テンソルの可視化
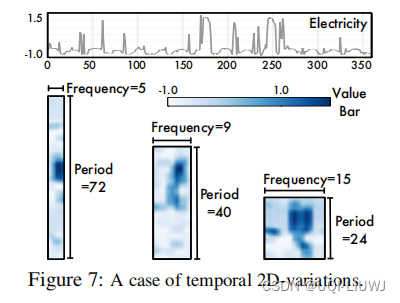
3.4 ハイパーパラメータの安定性

- 基本的には安定していますが、予測と異常検出では、k の選択が最終的なパフォーマンスに影響します。
3.5 アブレーション実験
3.5.1 Inception なしで他の畳み込みアーキテクチャを使用する

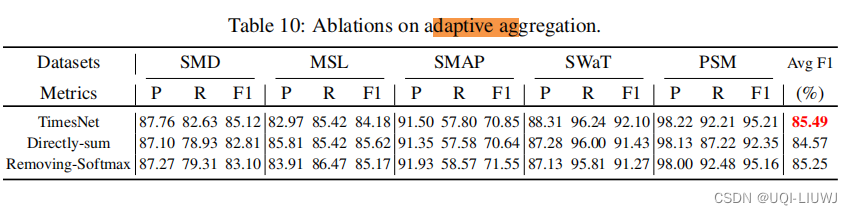
3.5.2 適応加算部
- 直接合計:得られた値を
直接合計する
- 合計の削除: Softmax なしで、直接
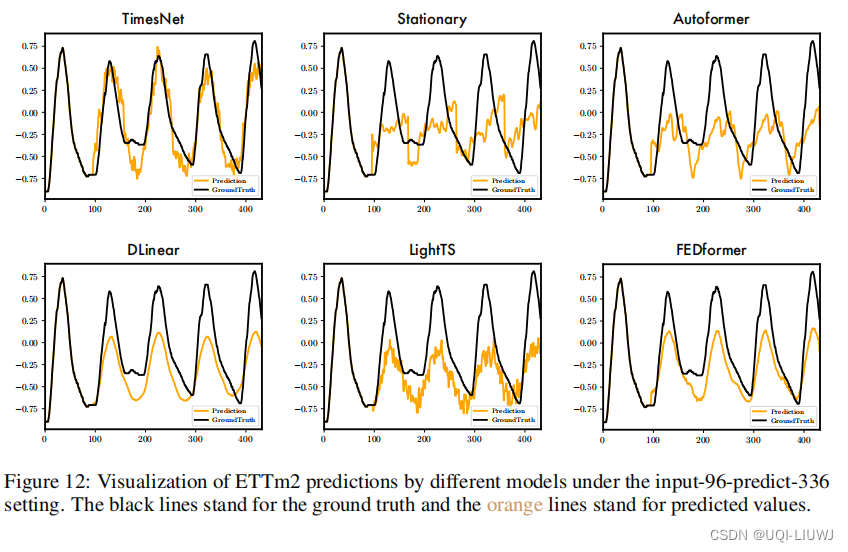
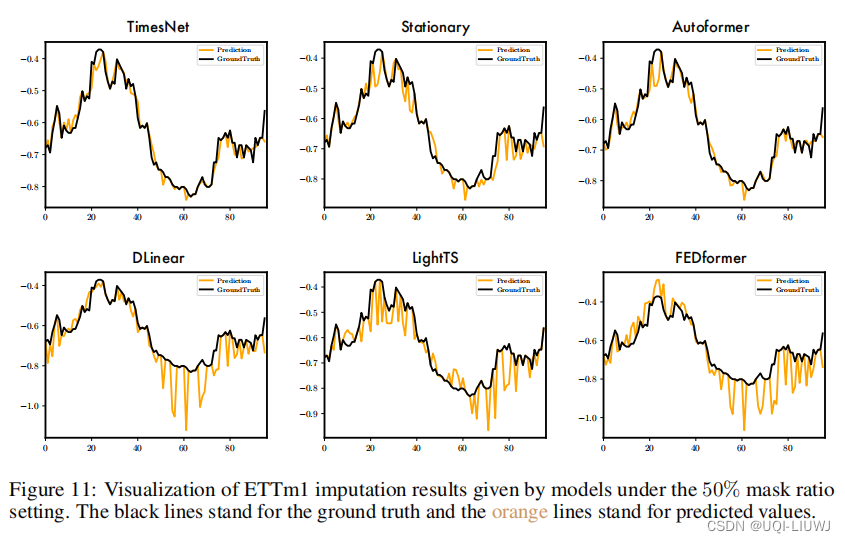
3.6 回帰効果の可視化
3.6.1 代入
3.6.2 予測