SciMLは単純な振り子の問題を解決します

振り子の問題は次のように表すことができます

$$\ddot{\theta }+\frac{}{L}\mathrm{それなし}\theta =0$$

その中で、$g$は重力加速度です;$L$は振り子の長さです;$\theta$はスイング角度であり、この方程式の分析解はありません。

角度が比較的小さい場合、$\sin （\theta ）\approx \theta$の場合、振り子の問題は線形形式に還元できます

$$\ddot{\theta }+\frac{}{L}\theta =0$$

角度が大きい場合、数値的に解くことができます。まず、それを一階微分方程式のシステムに分割します

$$\begin{array}{rl}& \dot{\theta }=\omega \\ & \dot{\omega }=-\frac{}{L}\mathrm{それなし}\end{array}$$

using OrdinaryDiffEq, Plots
plotlyjs()

const g = 9.81  #g是常量
L = 1.0

u₀ = [0,π/2]
tspan = (0.0,6.0)

#定义问题
function simplependulum(du,u,t)
    θ = u[1]
    ω = u[2]        #\omega + tab = ω
    du[1] = ω
    du[2] = -(g/L)*sin(θ)
end

prob = ODEProblem(simplependulum, u₀, tspan)
sol = solve(prob,Tsit5())

# plotlyjs绘图面板中有个相机的图标，点击可保存图片
plot!(sol, title ="钟摆问题", xaxis = "时间", label = ["θ" "ω"])

写真が示すように

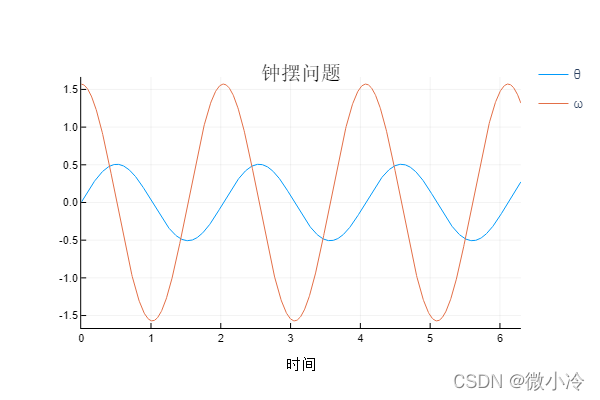
その中にTsit5は、崩壊曲線を解くために以前に使用されたが、説明されていない一次非線形微分方程式のシステムのソルバーがあります。Tsit5これは、SciML、5次のTsitouras法、および改良されたRunge-Kutta法によって推奨される推奨ソルバーです。

物理学では、時間の経過に伴う物理量の関係を確立することに加えて、物理量の関係、特に速度と座標の関係を確立する必要がある場合があります。これは、一般に位相空間として知られる、システムのすべての可能な状態を構成します。

3次元空間では、速度と運動量はそれぞれ3つの方向を持っているため、3次元空間の位相空間は一般に6つの次元を持ちます。ただし、ぐらつきの問題の場合、速度と位置を1次元に減らすことができるため、位相空間には2次元があります。

描画空間にも2次元があるため、線のみを描画できます。つまり、位相空間から描画できる線は一部のみです。

p = plot(sol,vars = (1,2), xlims = (-15,15), title = "相空间", xaxis = "速度", yaxis = "位置", leg=false)
# 用于绘图的函数
function phase_plot(func, u0, p)
    prob = ODEProblem(func,u0,(0.0,2pi))
    sol = solve(prob,Vern9()) # Vern9精度更高
    plot!(p,sol,vars = (1,2))
end
for i in -4pi:pi/2:4π
    for j in -4pi:pi/2:4π
        phase_plot(simplependulum, [j,i], p)
    end
end
plot(p,xlims = (-15,15))

結果は次のとおりです。