1.タイトルリンク：
フィボナッチ合計
2.トピックの主なアイデア：
物乞い
3.分析：
ゲーム中、Du Jiao BMはwaを維持しましたが、ゲーム後、モジュラスが間違っていることがわかりました...
Dujiao BMは、テンプレートを直接配置して係数を変更することでACにできるため、ここではDujiao BM以外のソリューションのみを示します（Dujiao BMはそれを気に入らないのですか？
最初にシンボルの説明を行います
シンボル化後、タイトルが必要です
次に、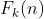
再帰式を見つけ ます
計算するとき 、以前の
値が計算されているので、必要なのは
次の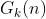
再帰式を求めています
とき の時間
とき の時間
この時点で、マトリックスを使用してパワーをすばやく解決できます
具体的には
知っている
再帰計算は知っています
4.コードの実装：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M = (int)1e2 + 4;
const ll mod = (ll)998244353;
const int inf = 0x3f3f3f3f;
const double eps = 1e-8;
ll n; int k;
ll g[M + 5];
ll f[M + 5];
struct node
{
ll D[M + 5][M + 5];
};
ll quick(ll a, ll b)
{
ll sum = 1;
while(b)
{
if(b & 1) sum = sum * a % mod;
a = a * a % mod;
b >>= 1;
}
return (sum + mod) % mod;
}
node mul(node a, node b)
{
node c; memset(c.D, 0, sizeof(c.D));
for(int i = 0; i < M; ++i)
for(int j = 0; j < M; ++j)
for(int l = 0; l < M; ++l)
c.D[i][j] = (c.D[i][j] + a.D[i][l] * b.D[l][j] % mod) % mod;
return c;
}
node quick(node a, ll b)
{
node sum; memset(sum.D, 0, sizeof(sum.D));
for(int i = 0; i < M; ++i) sum.D[i][i] = 1;
while(b)
{
if(b & 1) sum = mul(sum, a);
a = mul(a, a);
b >>= 1;
}
return sum;
}
int main()
{
// freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
scanf("%lld %d", &n, &k);
node A, B;
memset(A.D, 0, sizeof(A.D));
memset(B.D, 0, sizeof(B.D));
A.D[0][k] = 1, A.D[0][k + 1] = 2, A.D[0][k + 2] = 1, A.D[0][k + 3] = 1;
for(int j = k; j >= 0; --j)
{
B.D[k][j] = 1;
for(int i = k - 1; i >= j; --i) B.D[i][j] = (B.D[i][j + 1] + B.D[i + 1][j + 1]) % mod;
}
B.D[k][k] = 0;
B.D[k + 1][k] = B.D[k + 1][k + 1] = B.D[k + 1][k + 2] = 1;
B.D[k + 2][k] = B.D[k + 2][k + 1] = 1;
B.D[k + 3][k] = -1, B.D[k + 3][k + 3] = 1;
node G = mul(A, quick(B, n - 1));
for(int i = 0; i <= k; ++i) g[i] = G.D[0][k - i];
f[0] = G.D[0][k + 1] - 1;
for(int i = 1; i <= k; ++i)
{
f[i] = g[i];
for(int j = 0; j <= i - 1; ++j) f[i] = (f[i] + (((j&1)<<1)-1) * B.D[k - j][k - i] * quick(n % mod, i - j) % mod * f[j] % mod) % mod;
if(i & 1) f[i] *= -1;
f[i] = (f[i] + mod) % mod;
}
printf("%lld\n", f[k]);
return 0;
}