1. Vue d'ensemble
Je pense que beaucoup de gens peuvent trouver la transformation de Fourier complexe et un peu difficile à comprendre. En fait, ce n'est pas difficile, c'est juste une transformation intégrale .
La transformée de Fourier signifie qu'une fonction qui satisfait certaines conditions peut être exprimée comme une combinaison linéaire de fonctions trigonométriques (fonctions sinus et/ou cosinus) ou de leurs intégrales. C'est-à-dire que « n'importe quelle » fonction peut être exprimée comme une combinaison linéaire de fonctions sinusoïdales grâce à une certaine décomposition. La fonction sinusoïdale est une classe de fonctions bien étudiée et relativement simple en physique. Parce qu'elle est si simple à utiliser, la transformée de Fourier est largement utilisée en physique, théorie des nombres, mathématiques combinatoires, traitement du signal, probabilités, statistiques, cryptographie, acoustique, optique et dans d'autres domaines.
Pourquoi utiliser une courbe sinusoïdale pour décomposer la fonction d'origine ?
En raison de la fidélité de la sinusoïde. Après l'entrée d'un signal sinusoïdal, la sortie est toujours un signal sinusoïdal. Seules l'amplitude et la phase peuvent changer, mais la fréquence et la forme d'onde restent les mêmes. Et seules les courbes sinusoïdales ont de telles propriétés, nous allons donc décomposer la fonction originale en fonction sinusoïdale pour le traitement.
2. Transformée de Fourier continue, CFT
Si la transformée de Fourier que l'on voit habituellement n'a pas de préfixe, elle fait généralement référence à la transformée de Fourier continue. Regardons d'abord une image :

D'après l'image, nous pouvons comprendre que la transformée de Fourier est la conversion mutuelle du domaine temporel et du domaine fréquentiel. Comme elle est continue, elle utilise l'intégrale.
La musique que nous entendons habituellement est un mélange de différents sons, d'instruments de musique et de voix humaines qui changent avec le temps. Si je veux extraire la voix humaine seule, nous pouvons utiliser Fourier à ce moment-là. La transformation est utilisée pour décomposer ces différents sons en formes représentées. par leurs fréquences respectives. De cette façon, nous convertissons le signal du domaine temporel initialement difficile à traiter en un signal du domaine fréquentiel facile à traiter (spectre du signal), puis utilisons certains outils pour traiter et traiter ces signaux du domaine fréquentiel. Enfin, la transformée de Fourier inverse peut être utilisée pour convertir ces signaux dans le domaine fréquentiel en signaux dans le domaine temporel.
3. Transformée de Fourier discrète, DFT
En fait, notre ordinateur ne peut traiter que des signaux numériques discrets, ce qui est différent des calculs mathématiques. Ces sons continus doivent être traités de manière discrète, car les ordinateurs ne peuvent essentiellement traiter que 0 et 1, donc ici l'intégrale ne peut pas être utilisée. Nous savons que l'intégrale est en fait, la sommation continue de la limite, n'est-ce pas ? Alors nous ne pouvons utiliser ici que la sommation discrète, et elle ne peut pas gérer l'infini. L'ordinateur ne peut gérer que la finitude. C'est une condition préalable. Regardons une image :
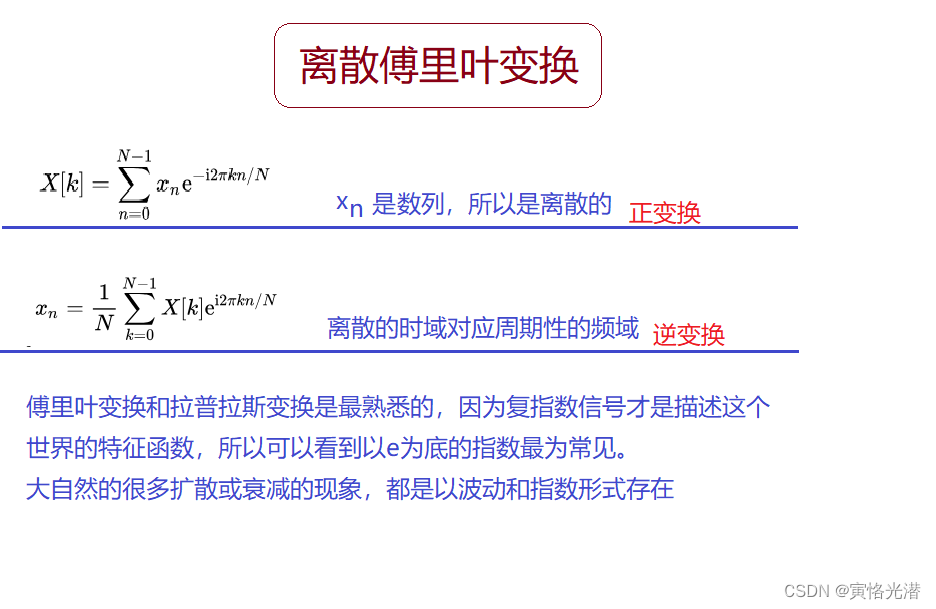
Vous pouvez voir que notre Fourier discret utilise le symbole de sommation au lieu du symbole intégral ci-dessus. Dans l'ordinateur, nous utilisons cette DFT pour traiter les signaux.
La complexité informatique de l'utilisation directe de la définition de DFT est O(N²), tandis que la transformation de Fourier rapide (FFT) peut améliorer la complexité jusqu'à O(nlogn). La réduction de la complexité informatique et le développement des capacités de calcul des circuits numériques ont fait de la DFT une méthode très pratique et importante dans le domaine du traitement du signal.
D'après l'analyse ci-dessus, nous savons que l'analyse dans le domaine temporel et l'analyse dans le domaine fréquentiel sont deux surfaces d'observation des signaux. L'analyse du domaine temporel utilise l'axe du temps comme coordonnée pour exprimer la relation des signaux dynamiques ; l'analyse du domaine fréquentiel modifie le signal sur l'axe des fréquences comme coordonnée pour l'exprimer.
De manière générale, la représentation du domaine temporel est plus vivante et intuitive, tandis que l'analyse du domaine fréquentiel est plus concise, ce qui rend l'analyse des problèmes plus approfondie et plus pratique. La tendance de l’analyse du signal se développe du domaine temporel au domaine fréquentiel. Cependant, ils sont interconnectés, indispensables et complémentaires les uns des autres. Leur conversion est ce que nous appelons la transformée de Fourier.
4. Application MATLAB
Jetons un coup d'œil à l'application spécifique. À quoi ressemblera-t-elle en utilisant la transformation de Fourier rapide FFT dans MATLAB.
Regardons d'abord la définition de la fonction fft :
Y = fft(X) calcule la transformée de Fourier discrète (TFD) de X à l'aide de l'algorithme de transformée de Fourier rapide (fft).
Si X est un vecteur, fft(X) renvoie la transformée de Fourier de ce vecteur.
Si X est une matrice, fft(X) traite les colonnes de X comme des vecteurs et renvoie la transformée de Fourier de chaque colonne.
Si X est un tableau multidimensionnel, fft(X) traite les valeurs le long de la première dimension du tableau dont la taille n'est pas égale à 1 comme vecteurs et renvoie la transformée de Fourier de chaque vecteur.Y = fft(X,n) renvoie une DFT à n points. Si aucune valeur n'est spécifiée, Y a la même taille que X.
Si X est un vecteur et que la longueur de X est inférieure à n, alors X est complété par des zéros à droite pour atteindre la longueur n.
Si X est un vecteur et que la longueur de X est supérieure à n, alors X est tronqué à la longueur n.
Si X est une matrice, chaque colonne est traitée de la même manière que dans le cas vectoriel.
Si X est un tableau multidimensionnel, la première dimension du tableau dont la taille n'est pas égale à 1 est traitée de la même manière que dans le cas vectorielY = fft(X,n,dim) renvoie la transformée de Fourier le long de la dimension dim. X est une matrice, par exemple :
fft(X,n,1) opère sur chaque colonne de X et renvoie la transformée de Fourier de chaque colonne ;
fft(X,n,2) opère sur chaque ligne de X et renvoie la transformée de Fourier de chaque transformée de Fourier en ligne.
4.1. Signal de bruit
Regardons un exemple concret d'utilisation de la transformée de Fourier pour trouver les composantes fréquentielles d'un signal cachées dans le bruit (analyse spectrale).
Fs = 1000; %采样频率
T = 1/Fs; %采样周期
L = 1500; %信号长度(1.5秒)
t = (0:L-1)*T; %时间
%创建一个信号,其中包含幅值为0.7,频率为50Hz和幅值为1,频率为120Hz的正弦波
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
%添加一个标准差为2的噪声
X = S + 2*randn(size(t));
%绘制噪声时域信号。
plot(1000*t(1:50),X(1:50))
title('加了噪声的信号')
xlabel('t (毫秒)')
ylabel('X(t)')
En regardant ce signal du domaine temporel
%计算双侧频谱P2,然后基于P2和偶数信号长度L计算单侧频谱P1,单侧频谱表示信号频率的幅度分布只从0到正频率一侧,正负频率是对称的
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);Les abs renvoient ici des valeurs absolues, mais ici ils sont sous la forme de nombres complexes , ce qui est donc renvoyé est leur longueur de module (amplitude) , qui représente la taille des nombres complexes. Il existe un autre attribut important pour les nombres complexes, qui est la phase, qui représente plusieurs directions.
Faisons un dessin pour voir l’amplitude correspondante du spectre :
f = Fs*(0:(L/2))/L;
plot(f,P1)
title('单侧幅值频谱')
xlabel('f (Hz)')
ylabel('|P1(f)|')Vous pouvez voir qu'à 50 Hz et 120 Hz , les amplitudes sont fondamentalement proches de 0,7 et 1. En raison de l'ajout de bruit , s'il n'y a pas de bruit, il doit correspondre à 0,7 et 1. Vous pouvez essayer ceci. Ici, nous pouvons voir que dans les coordonnées du domaine temporel, il est difficile de visualiser la composante fréquentielle du signal. Lorsque nous utilisons la transformée de Fourier, il devient simple de visualiser le signal dans le domaine fréquentiel.
4.2. Impulsions gaussiennes
La soi-disant impulsion consiste à envoyer un signal, à l'allumer et à l'éteindre, c'est une impulsion. Les moteurs pas à pas et les servomoteurs d'aujourd'hui sont entraînés par des impulsions.
Une impulsion gaussienne est une impulsion avec une courbe temps-intensité de forme gaussienne, où la fonction gaussienne est la suivante :
Parmi eux, a, b et c sont des constantes. a détermine la hauteur de la courbe (valeur maximale), b détermine la position centrale de la courbe (abscisse) et c détermine la largeur de la courbe (écart type).
Étant donné que la courbe d'intensité temporelle de l'impulsion gaussienne présente les caractéristiques de la distribution gaussienne, elle permet d'obtenir de meilleures performances en temps et en fréquence et a été largement utilisée dans de nombreux domaines.
Jetons un coup d'œil à la manière dont les impulsions gaussiennes sont transférées du domaine temporel au domaine fréquentiel :
Fs = 100; %采样频率
t = -0.5:1/Fs:0.5; %时间
L = length(t); %信号长度
%高斯脉冲对应上面公式中的a、b、c了解
X = 1/(4*sqrt(2*pi*0.01))*(exp(-t.^2/(2*0.01)));
%画图
plot(t,X)
title('时域中的高斯脉冲')
xlabel('Time (t)')
ylabel('X(t)')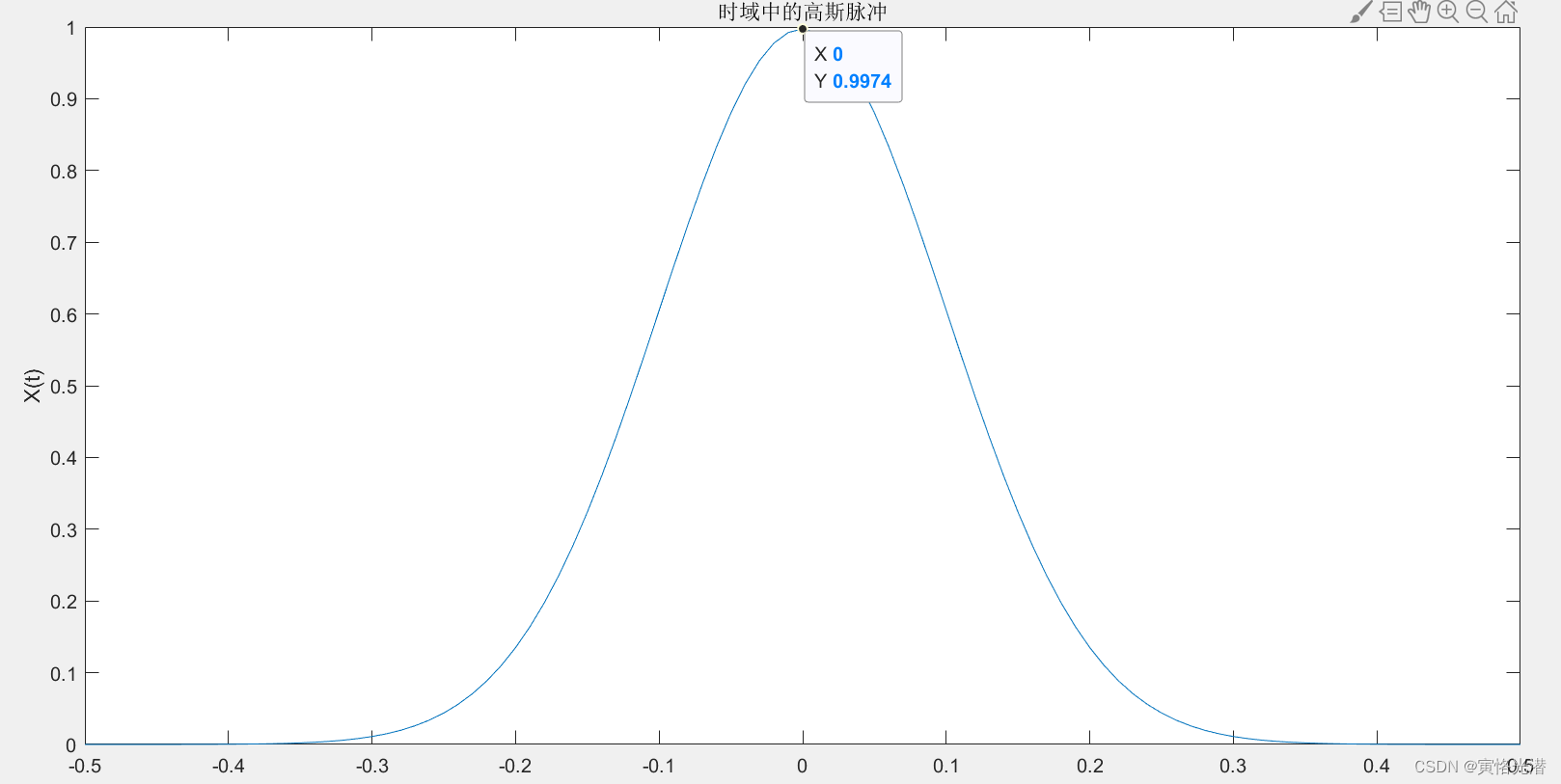
Sur le graphique, nous pouvons voir qu'il s'agit d'une distribution gaussienne avec un point central de 0 et une valeur maximale d'environ 0,9974. De plus, la formule montre que la largeur est de 0,1. Cette fonction est une fonction caractéristique typique de la transformée de Fourier.
Avant la conversion dans le domaine fréquentiel, la nouvelle longueur d'entrée, qui est la prochaine puissance de 2, est d'abord déterminée à partir de la longueur du signal d'origine. Lorsque la longueur du signal n'est pas égale à une puissance de 2, l'utilisation de la fonction nextpow2 peut améliorer les performances de fft, en utilisant des zéros à droite pour remplir le signal.
n = 2^nextpow2(L);
%将高斯脉冲转换为频域。
Y = fft(X,n);%length(X):101,n:128,所以length(Y)是128
%画图
f = Fs*(0:(n/2))/n;
P = abs(Y/n);
plot(f,P(1:n/2+1))
title('频域中的高斯脉冲')
xlabel('Frequency (f)')
ylabel('|P(f)|')
La fonction nextpow2 dans le code renvoie l'exposant de la prochaine puissance de 2 supérieure ou égale à ces valeurs (valeur absolue), par exemple :
a = [1 -2 3 -4 5 9 519];
p = nextpow2(a)
p =
0 1 2 2 3 4 10
2.^p 或者 pow2(p)
ans =
1 2 4 4 8 16 1024
4.3, onde cosinusoïdale
Jetons un coup d’œil à l’une des formes d’onde les plus courantes et comparons leurs différentes fréquences :
Fs = 1000; %采样频率
T = 1/Fs; %采样周期
L = 1000; % 信号长度
t = (0:L-1)*T; % 时间
%三个余弦波,区别就是频率不一样
x1 = cos(2*pi*50*t); %50Hz
x2 = cos(2*pi*150*t); %150Hz
x3 = cos(2*pi*300*t); %300Hz
% 组合成一个矩阵
X = [x1; x2; x3];
%画出每个余弦波前100个条目
for i = 1:3
subplot(3,1,i)
plot(t(1:100),X(i,1:100))
title(['余弦波 ',num2str(i),' 的时域图形'])
end
Ici, nous trouvons trois ondes cosinusoïdales. Nous pouvons seulement dire que la fréquence de l'onde cosinusoïdale descendante est supérieure à celle de l'onde supérieure, mais elle ne peut toujours pas montrer clairement son essence. Convertissons-la dans l'espace du domaine fréquentiel pour voir quel effet est:
%同样的性能考虑,使用nextpow2函数定义新长度
n = 2^nextpow2(L);
%接下来就计算傅里叶变换
dim = 2;
Y = fft(X,n,dim);
%计算每个信号的双侧频谱和单侧频谱
P2 = abs(Y/L);
P1 = P2(:,1:n/2+1);
P1(:,2:end-1) = 2*P1(:,2:end-1);
%在频域图形里面,画出每一个余弦波的单侧幅值频谱
for i=1:3
subplot(3,1,i)
plot(0:(Fs/n):(Fs/2-Fs/n),P1(i,1:n/2))
title(['余弦波 ',num2str(i),'在频域中的图形'])
end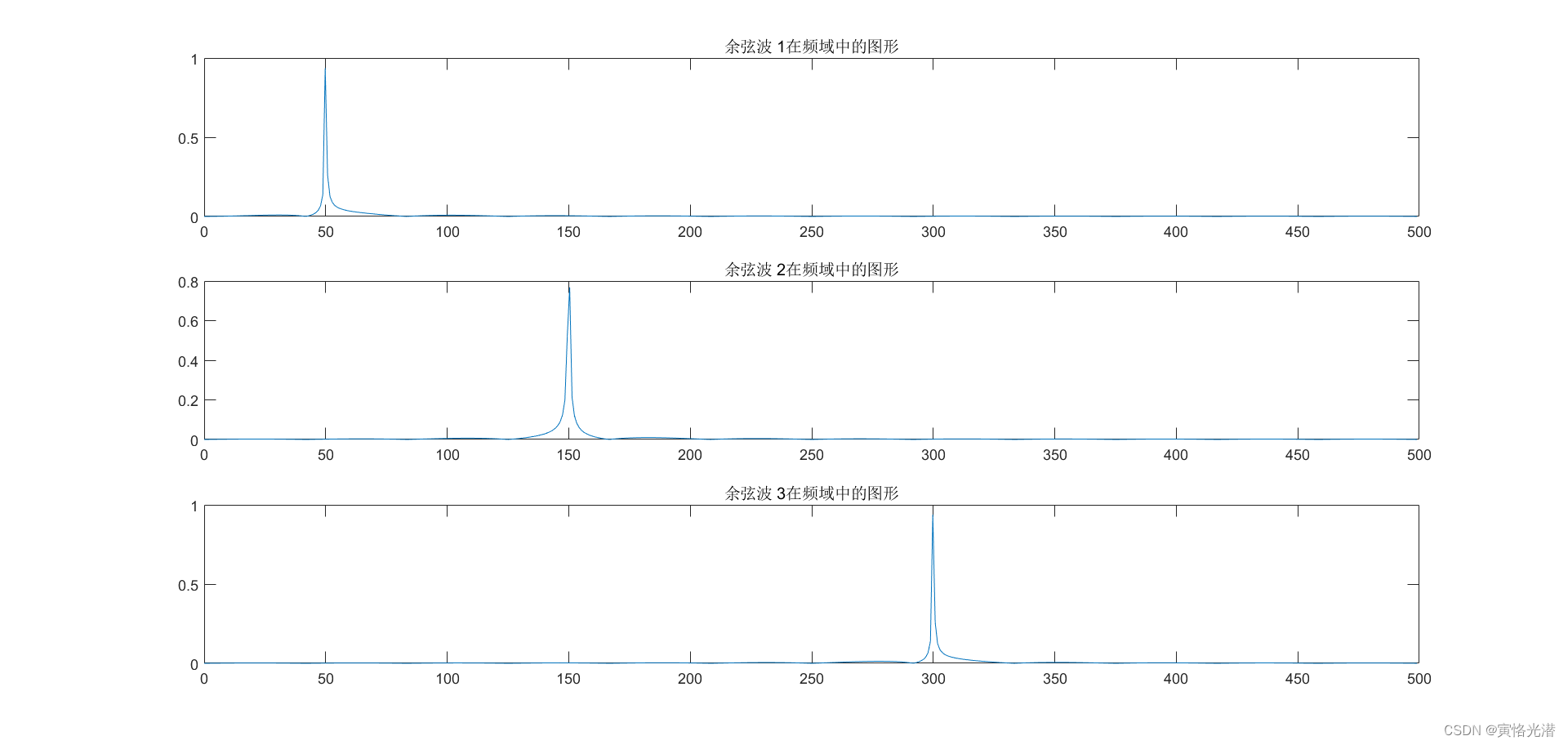
Nous pouvons voir qu'une fois le domaine temporel converti en domaine fréquentiel, le problème devient simple et clair. Bien sûr, nous pouvons utiliser la première méthode de bruit pour les trois dernières ondes cosinusoïdales, ajouter les trois, puis convertir le domaine temporel en le domaine fréquentiel. Par comparaison, on constate que les signaux dans le domaine temporel sont plus difficiles à traiter, mais la transformation vers le domaine fréquentiel devient plus simple.
Transformée de Fourier d'une onde cosinusoïdale