Par exemple: une classe pour apprendre un total de 100, dont 30% du nombre élevé de branches pendantes, fils branches pendantes au nom de 25%, le nombre élevé de branches pendantes des élèves, les familles de la probabilité algébrique est liée à combien? (Note: le titre nombre et de l' algèbre en branches pendantes, quelle est la probabilité qu'il ya une différence, la différence est que l' on est en même temps la classe entière des taux de branches pendantes, qui est l'espace de l' échantillon est l'ensemble de la classe 100 étudiants, tandis que l'espace de l' échantillon est nombre de branches pendantes) la
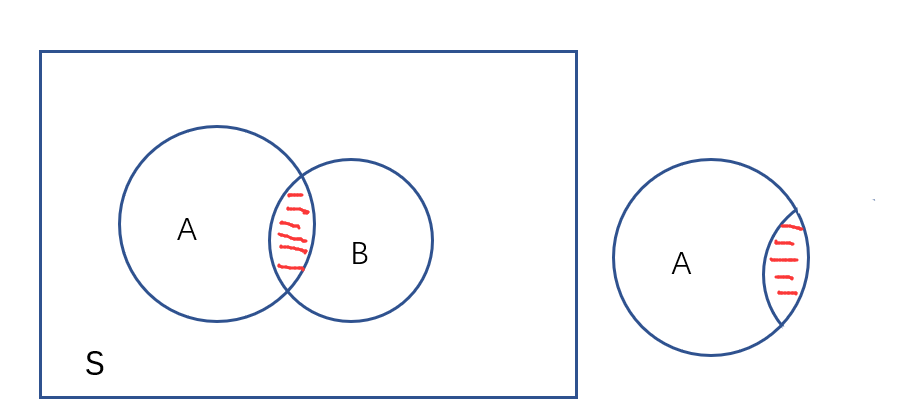
surface totale de l' échantillon est la suivante : s = 100
probabilité un de l'événement: le nombre de branches pendantes probabilité = 30%
probabilité d'événements B: ligne représente branches pendantes probabilité = 25%
dans le cas des branches pendantes du un, événement B la probabilité est la probabilité conditionnelle P (B | a) =
\ ({P \ left (B \ left |. A \ gauche) = \ frac {{P \ left (AB \ right)}} {{P \ left (A \ right)}} \ right \ right \ right. .} \)
- à -dire l'intersection de a et B divisée par l'espace d' un des points d'échantillonnage.
Exemples: on prévoit six rouge boîte à billes, quatre blancs. Extraction sans remplacement, chaque prise soit un total extrait deux fois.
1) pour prendre la première balle blanc connu, nécessite le calcul d' une deuxième probabilité à bille rouge.
2) prises pour trouver la première balle blanche, la deuxième probabilité pour obtenir la balle rouge.
Une hypothèse pour l'événement à prendre la bille rouge, pour la première fois « prendre la bille rouge » comme A1, le deuxième pompage du ballon à A2. Par rapport à l'événement correspondant A « pour obtenir boule blanche »
probabilité 1 en question de prendre d' abord la balle rouge, puis les neuf boules restantes, prises en boule rouge 9, à savoir:
\ ([{P \ left (\ texte {} A \ mathop {{ }} \ NoLimits _ {{2}} \ left | \ overline {A} \ mathop {{}} \ nolimits _ {{1}} \ left) = \ frac {{6}} { {9}} = \ frac {
{2}} {{3}} \ right \ right \ right} \) ... la différence entre les deux problèmes est un problème: un problème à un "connu", est les conditions décrites . la question 2 est calculé le calcul de l' étape commune.
\ ({\ begin {{tableau} * {20} est {l}} {P \ left (\ texte {} \ overline {a} \ {{mathop}} \ NoLimits _ {{1}} A \ mathop {{}} \ nolimits _ {{2}} \ left) = P \ left (\ texte {} \ overline {A} \ mathop {{}} \ nolimits _ {{1} } \ left) \ times P \ left (\ texte {} A \ mathop {{}} \ nolimits _ {{2}} \ left | \ overline {A} \ mathop {{}} \ nolimits _ {{1}} \ gauche) = \ frac {{4 }} {{10}} \ times de la frac {{2}} {{3}} = \ frac {{4}} {{15}} \ right. \ right. \ right . \ right. \ right. \ droite. \ right.} \\ {\ texte {} \ texte {} \ texte {}} \ end {array}} \)
Exemple 2: Supposons qu'il y ait trois billets de loterie, dont une seule est de gagner à la loterie, les trois étudiants à leur tour existants tirés sans remplacement, demandez à un camarade de classe finalement gagner la probabilité est plus petite que les autres étudiants.
À condition X = n'a pas gagné, y = gagner
de l' espace échantillon s = {YXX, xyx, XXY }, seulement trois cas. Enfin, une probabilité de gagner est de 1/3 ,
mais est connu pour les étudiants n'a pas gagné le premier, puis le reste de l'espace de l' échantillon est 2, la probabilité de gagner cette fois -ci dernier est un 1/2
Nature de la probabilité conditionnelle de
1) un non-négatif: pour chaque événement B, il y a P (B | A)> 0
2) Caractéristiques: pour l'événement inévitable s, il y a P (S | A) = 1
3) peut être ajouté à la colonne. de: Soit B1, B2 ... des événements par paires mutuellement exclusives, il
\ ({\ Begin {tableau} {* {20} {l}} {P \ left (\ mathop {{\ mathop {{\ tasse}} \ limits ^ {{\ infty}}}} \ limites _ {{i = 1}} ^ {{} } B \ mathop {{}} \ nolimits _ {{i}} \ left | A \ gauche) = {\ mathop {\ sum} \ limites _ {{i = 1}} ^ {{ \ infty}} {P \ left (B \ {mathop {} ...} \ nolimits _ {{i}} \ left | A \ right) \ right}} \ right \ right \ right} \\ {\ texte. {} \ texte {} \ texte
{}} \ end {array}} \) et la probabilité totale de tous les événements et les événements dans = la probabilité conditionnelle d'occurrence et.
Multiplication formule
\ ({\ begin {array} {* {20} {l}} {P \ left (AB \ left) = P \ left (B \ left | A \ gauche) \ fois P \ left (A \ droite ) \ right. \ right. \
droite. \ right. \ right.} \\ {\ texte {} \ texte {} \ texte {}} \ end {array}} \) On comprendra que comme la probabilité de AB simultanée = B probabilité de la probabilité d'occurrence de l'espace entier de l' échantillon a * se produit lorsque l'un de condition se produit.
Le type peut être généralisé à tracer des événements plus d' événements. Par exemple: Soit A, B, C pour l'événement, et P (AB)> 0, il y a P (ABC) = P (C | AB) P (B | A) P (A)
\ ({\ Begin {array} {* {20} {l}} {P \ left (AB \ left) = P \ left (B \ left | A \ gauche) \ fois P \ left (A \ droite) \ à droite. \ right. \ right. \ right. \ right.} \\ {P \ left (B \ left) = 0,4, P \ left (A + B \ gauche) = 0,5, \ texte {求} \ texte { } P \ left (A \ left | \ overline {B} \ left) \ texte {} \ texte {} \ right \ right \ right \ right \ right \ right \ right} {\\....... P \ left (A \ gauche) = 1-0,5 = 0,5 \ right. \ right.} \\ {P \ left (\ overline {B} \ left) = 1 à 0,4 = 0 \ texte {} 0,6 \ right . \ right} \\ {P \ left (A \ left | \ overline {B} \ left). = \ frac {{P \ left (A \ overline {B} \ right)}} {{P \ left ( \ overline {B} \ right)}} = \ frac {{0,1}} {{0,6}} = \ frac {{1}} {{6}} \ right. \ right. \ right.} \\ {\ texte {}} \\ {} \ end {array}} \)

Figure comprise
\ ({P \ left (A \ overline {B} \ right)} \) = A et B d'intersection de l'événement opposé, à savoir 0,1
第二种办法:公式推导
\ ({P \ left (A \ left | \ overline {B} \ left) = 1-P \ left (\ overline {A} \ left | \ overline {B} \ left) = 1- \ frac {{1-P \ left (A \ cup B \ right)}} {{1-P \ left (B \ right)}} = 1- \ frac {{1-0,5}} {{1 -0,4}} = \ frac {{1}} {{6}} \ right. \ right. \ right. \ right. \ right. \ right.} \)
Exemple 2: un mot de passe de la carte d'épargne d'un total de six chiffres, chaque chiffre peut choisir l' une de 0-9, retirer de l' argent dans la banque quelqu'un de distributeurs automatiques de billets, oublier le dernier mot de passe à deux chiffres, la recherche
1) selon l' une quelconque du dernier chiffre, pas plus de deux fois pour appuyer sur la probabilité.
Presse pour mettre en place des événements pour le A, pour la première fois par A1, A2 du secondaire par
pas plus de deux fois la probabilité de la presse, selon la première ou la deuxième paire sont considérés par pas plus de 2 fois par la droite.
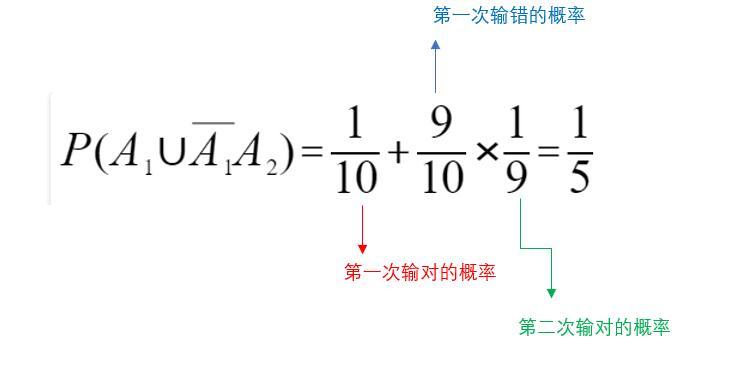
2) S'il se souvient du mot de passe dernier est un nombre pair, pas plus de 2 fois à la presse probabilité de
dessus est le même, mais l'espace de l' échantillon devient {0,2,4,6,8}, un total de cinq mots
\ ({{P \ left ( \ mathop {{A}} \ nolimits _ {{1}} \ cup \ overline {\ mathop {{A}} \ nolimits _ {{1}}} A \ mathop {{}} \ nolimits _ {{2}} \ gauche) = \ frac {{1}} {{5}} + \ frac {{4}} {{5}} \ times de la frac {{1}} {{4}} = \ frac {{2}} { {5}} \ right. \ right.}} \)
Exemple 3: Un taux d'échec de la classe Cours de 4%, tandis que les élèves passeront 25% des étudiants peuvent attendre A, trouver la probabilité de A à donner à l'étudiant.
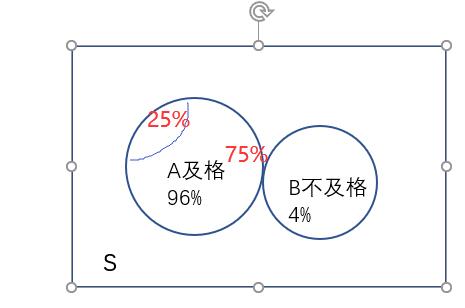
Événement A: avoir un événement B: pass
connu:
\ ({\ Array begin {} {} {L * 20 est {{}} A \ subset B, AB = A, P \ left (AB \ left) = P \ left (A \ right) \ droite. \ droite.} \\ {P \ left (B \ left) = 4/1 \ texte {%} = 96 \ texte {%} \ right. \ right.} \\ {P \ left (A \ left | B \ gauche) = 25 \ texte {%} \ right \ right \ right ...} \\ {P \ left (AB \ left) = P \ left (B \ left) \ fois P \ left (A \ gauche | B \ left) = 96 \ texte {%} \ times 25 \ texte {%} = 0,24 \ right \ right \ right \ right \ right \ right \ ...... à droite.} \ end {array} } \)