Introducción a la coherencia
La función de coherencia entre dos procesos aleatorios estacionarios generalizados![]() es igual a la raíz cuadrada del producto del espectro de potencia cruzada dividido por el espectro de potencia automática. Específicamente, la coherencia compleja se define como:
es igual a la raíz cuadrada del producto del espectro de potencia cruzada dividido por el espectro de potencia automática. Específicamente, la coherencia compleja se define como:![]()
![]()

donde el complejo espectro de potencia cruzada es
![]()
es la transformada de Fourier de la función de correlación cruzada
![]()
Aquí xey son números reales, y E representa la expectativa matemática (para procesos estocásticos ergódicos, el promedio establecido puede reemplazarse por el promedio de tiempo). La coherencia es una función de densidad espectral de potencia cruzada normalizada; la coherencia al cuadrado (MSC) se define como
![]()
![]()
La función de coherencia tiene aplicaciones en muchos campos, incluida la identificación de sistemas, la medición de la relación señal-ruido (SNR) y la determinación de retardo de tiempo. La coherencia, especialmente la coherencia cuadrática (MSC), sólo funciona si su valor puede estimarse con precisión. De hecho, es muy deseable comprender las estadísticas de los evaluadores. Por lo tanto, esta sección explicará la función de coherencia. Las siguientes secciones describen el proceso de estimación correcta de las estadísticas de MSC y estimadores.
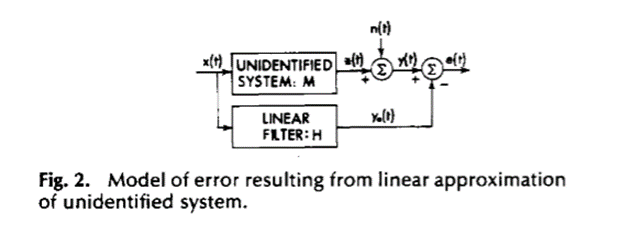
Una interpretación interesante de la coherencia -y del MSC en particular- es una medida de la linealidad relativa de los dos procesos. Para ilustrar esto, considere la Figura 1:

La función muestral y(t) de cualquier proceso aleatorio estacionario ![]() consta de la respuesta del filtro lineal más el componente de error e(t). Cuando se elige un filtro lineal para minimizar el valor cuadrático medio de e(t), es decir, el área bajo el espectro de error, se
consta de la respuesta del filtro lineal más el componente de error e(t). Cuando se elige un filtro lineal para minimizar el valor cuadrático medio de e(t), es decir, el área bajo el espectro de error, se ![]() convierte en la parte de y(t) que está linealmente relacionada con x(t). Las características espectrales de e(t) vienen dadas por:
convierte en la parte de y(t) que está linealmente relacionada con x(t). Las características espectrales de e(t) vienen dadas por:
![]()
![]()
En la fórmula, * representa el conjugado complejo y H(f) es la función de transferencia del filtro. El espectro de error es:

Por lo tanto, el filtro óptimo está dado por
![]()
Tenga en cuenta que la coherencia está asociada con filtros lineales óptimos.

Estos resultados se mantienen independientemente de la fuente de y(t). Cuando el filtro lineal es óptimo en el sentido cuadrático medio, el error no tiene nada que ver con x(t), es decir:
![]()
Además, ![]() el valor mínimo de viene dado por:
el valor mínimo de viene dado por:
![]()
![]()
![]()
Como puede verse
![]()
Representa MSC como la proporción en el componente lineal de y(t) ![]() ,
, ![]() que es la proporción en el error
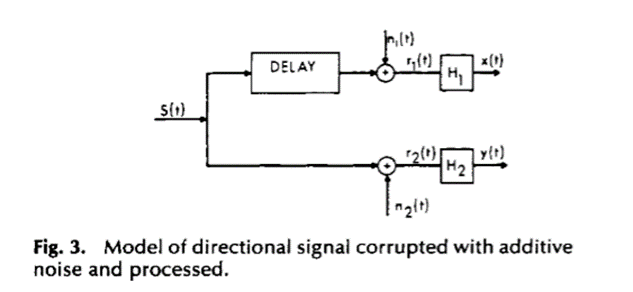
que es la proporción en el error ![]() , es decir, el componente no lineal de y(t). Estos resultados se pueden aplicar a las configuraciones que se muestran en las Figuras 2 y 3.
, es decir, el componente no lineal de y(t). Estos resultados se pueden aplicar a las configuraciones que se muestran en las Figuras 2 y 3.
Análisis estadístico de la estimación de MSC mediante el promedio segmentado de superposición de Welch (WOSA)
A.Introducción _
Gran parte del trabajo histórico sobre estadísticas de estimación de MSC se centra en el método WOSA; con una interpretación razonable de las variables, estos resultados también son aplicables al método de remodelación lager. Recordemos que el método WOSA consiste en obtener dos series de tiempo finitas del proceso estocástico investigado. Cada serie temporal se divide en segmentos de igual longitud y se muestrean en puntos de datos igualmente espaciados. Los fragmentos se superponen. Sin embargo, las estadísticas son una parte no superpuesta del desarrollo analítico. Se dan resultados empíricos para segmentos superpuestos. Las muestras de cada segmento se multiplican por una función de ponderación y luego se realiza una FFT de la secuencia ponderada. Luego se utilizan los coeficientes de Fourier de cada segmento ponderado para estimar la densidad espectral de potencia automática y la densidad espectral de potencia cruzada. La estimación de densidad espectral resultante se utiliza para formar la estimación de MSC.
La resolución espectral de la estimación varía inversamente con la longitud del segmento t. La ponderación o "ventana" adecuada de t segundos también puede ayudar a lograr una buena reducción de los lóbulos laterales. Por otro lado, para segmentos independientes con ventanas ideales, el sesgo y la varianza de las estimaciones de MSC son inversamente proporcionales al número de segmentos n. Por lo tanto, para producir buenas estimaciones con datos limitados, se puede aumentar la superposición de segmentos para n y t. Cuando los segmentos no se cruzan, es decir, no se superponen, lo llamamos número de segmentos ![]() . Sin embargo, a medida que aumenta el porcentaje de superposición, los requisitos computacionales aumentan rápidamente, mientras que la mejora se estabiliza debido a la mayor correlación entre los segmentos de datos.
. Sin embargo, a medida que aumenta el porcentaje de superposición, los requisitos computacionales aumentan rápidamente, mientras que la mejora se estabiliza debido a la mayor correlación entre los segmentos de datos.
B. Densidad de probabilidad estimada por MSC
Las funciones estimadas de densidad de probabilidad de primer orden y distribución de MSC se dan en la Tabla 1, dado el valor real de MSC y el número de segmentos independientes nd![]() . Simbólicamente, recuerda
. Simbólicamente, recuerda ![]() . Las ecuaciones (1b) y (1c) de esta tabla son útiles porque la
. Las ecuaciones (1b) y (1c) de esta tabla son útiles porque la ![]() función hipergeométrica “ ” es
función hipergeométrica “ ” es ![]() un polinomio de orden ( ).
un polinomio de orden ( ).

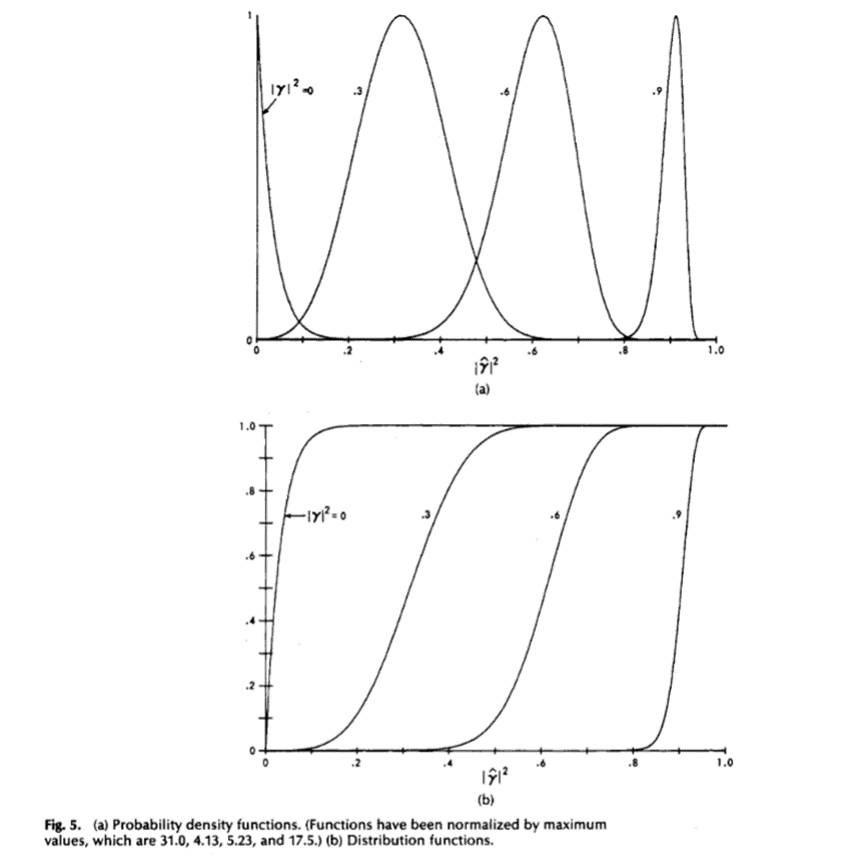
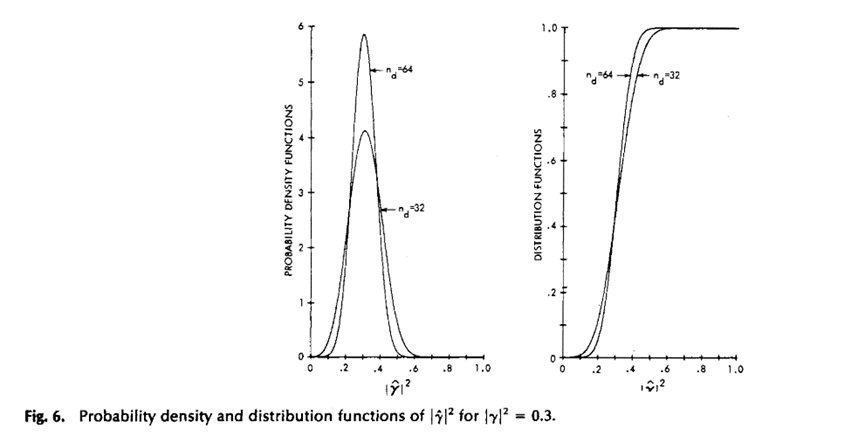
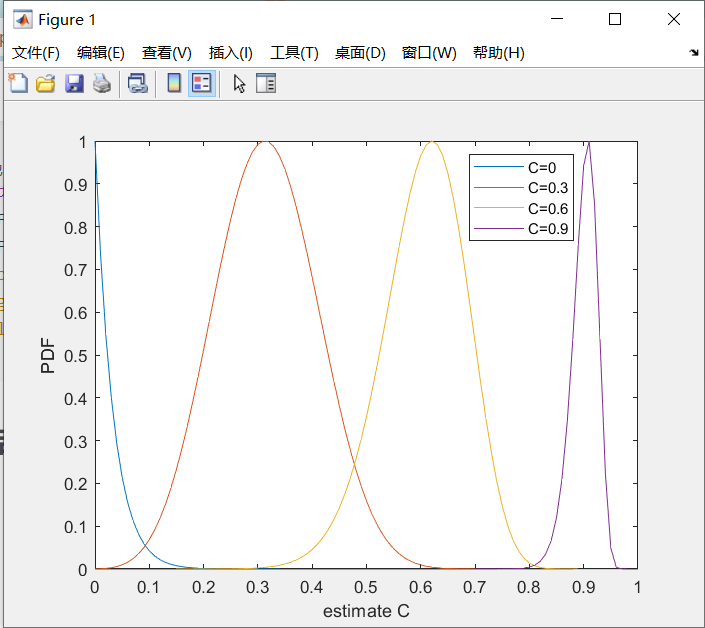
Las Figuras 5 y 6 muestran las funciones de densidad y distribución de probabilidad en varios casos, calculadas a partir de (1b) y (1d) en la Tabla 1. De la Figura 6 se desprende claramente que cuando ![]() aumenta, la varianza de la estimación de MSC disminuye.
aumenta, la varianza de la estimación de MSC disminuye.
Las expresiones de sesgo y varianza obtenidas se muestran en la Tabla 2. Las aproximaciones (2c) y (2d) son el resultado de truncar las secuencias (2a) y (2b). Las ecuaciones (2e) a (2g) se aplican a los grandes ![]() ; muestran que la estimación del MSC es asintóticamente insesgada y
; muestran que la estimación del MSC es asintóticamente insesgada y ![]() se pueden extraer las siguientes conclusiones para los grandes.
se pueden extraer las siguientes conclusiones para los grandes.
1) Cuando MSC es igual a 0, la desviación es la más grande, y ![]() cuando MSC es igual a 1, la desviación es la más pequeña, que es 0.
cuando MSC es igual a 1, la desviación es la más pequeña, que es 0.
2) Cuando MSC es igual a 1, la varianza es 0. Cuando MSC es igual a 1/3, la desviación es la mayor ![]() .
.
3) Si MSC no es cero, el error cuadrático medio del valor verdadero es igual a la varianza.
 Código relacionado
Código relacionado
clear
%实际的MSC分别为0,0.3,0.6,0.9时的概率密度函数(PDF)和累积分布函数(CDF)
nd=32;C_list=[0 0.3 0.6 0.9];
estimate_C=0:0.01:1;%估计的MSC
figure(1)
for i=1:length(C_list)
C=C_list(i);
PDF=(nd-1)*((1-C).^nd)*((1-estimate_C).^(nd-2))...
.*((1-C.*estimate_C).^(1-2*nd))...
.*(hypergeom([1-nd,1-nd],1,C*estimate_C));
PDF=PDF/max(PDF);
plot(estimate_C,PDF);xlabel('estimate C');ylabel('PDF')
legend('C=0', 'C=0.3', 'C=0.6', 'C=0.9');
hold on
end
figure(2)
for j=1:length(C_list)
C=C_list(j);
CDF1=hypergeom([0,1-nd],1,C*estimate_C);%当k=0时
for k=1:nd-2
CDF1=CDF1+(((1-estimate_C)./(1-C*estimate_C)).^k)...
.*hypergeom([(-k),1-nd],1,C*estimate_C);
end
CDF=estimate_C.*(((1-C)./(1-C*estimate_C)).^nd).*CDF1;
CDF=CDF/max(CDF);
plot(estimate_C,CDF);xlabel('estimate C');ylabel('CDF')
legend('C=0', 'C=0.3', 'C=0.6', 'C=0.9');
hold on
end
%C=0.3;nd分别为32和64时的PDF和CDF
estimate_C=0:0.01:1;
C=0.3;nd_list=[32 64];
figure(3)
for i=1:length(nd_list)
nd=nd_list(i);
PDF=(nd-1)*((1-C).^nd)*((1-estimate_C).^(nd-2))...
.*((1-C.*estimate_C).^(1-2*nd))...
.*(hypergeom([1-nd,1-nd],1,C*estimate_C));
plot(estimate_C,PDF);xlabel('estimate C');ylabel('PDF')
legend('nd=32', 'nd=64');
hold on
end
figure(4)
for j=1:length(nd_list)
nd=nd_list(j);
CDF1=hypergeom([0,1-nd],1,C*estimate_C);%当k=0时
for k=1:nd-2
CDF1=CDF1+(((1-estimate_C)./(1-C*estimate_C)).^k)...
.*hypergeom([(-k),1-nd],1,C*estimate_C);
end
CDF=estimate_C.*(((1-C)./(1-C*estimate_C)).^nd).*CDF1;
CDF=CDF/max(CDF);
plot(estimate_C,CDF);xlabel('estimate C');ylabel('CDF')
legend('nd=32', 'nd=64');
hold on
end
Resultados de la simulación



Si tiene alguna pregunta, deje un mensaje ~~