Análisis geoespacial del transporte - Lección 1: Gráficos y redes

Este documento son mis notas de clase.

Estrictamente hablando, debido a que la mitad de las notas son contenido del material didáctico del maestro, simplemente le agregué mi propia comprensión y explicación, por lo que mi maestro completó la mitad de la creación del contenido de esta nota.

• Este curso trata principalmente sobre algunos métodos prácticos de análisis geoespacial.
• Más que la teoría, me importa más cómo implementarla.
• Lo combiné con Python que suelo utilizar para explicar y resolver problemas.
• Basado en el cuaderno Jupyter

Compártelo aquí, espero que pueda ayudar a algunas personas.

Horas de clase: 32 horas (1-16 semanas, 8 semanas de clases experimentales)

Requisitos del curso:

1. Comprender los conocimientos teóricos relacionados con la topología de la red de transporte.
2. Dominar las operaciones del software de información geográfica (SIG) (mapinfo, etc.)
3. Tener ciertas capacidades de programación (mapbasic, etc.)

En esta nota, para familiarizarme con algunos métodos operativos prácticos, usaré Python para hacer algunos ejemplos, incluido el dibujo y algunos métodos de procesamiento de datos.

Estas son las bibliotecas y configuraciones de dibujo utilizadas en esta nota:

import numpy as np 
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt

plt.rcParams.update({
    
    
    # "figure.figsize":(8, 6),
    "font.sans-serif":'SimHei',
    "figure.dpi":100,
    "axes.unicode_minus":False,
    "image.cmap":'viridis'
})

La imagen es el modelo más intuitivo.

• La teoría de grafos es una herramienta importante en el análisis de sistemas de transporte.
• La teoría de grafos juega un papel importante en la planificación y gestión del sistema de transporte .
• La teoría de grafos es un medio importante para el análisis abstracto de las redes de transporte reales.

En general, el método de la teoría de grafos es la forma más intuitiva de expresar la red de transporte .

La historia de la teoría de grafos.

• Problema de los siete puentes de Königsberg (circuito euleriano)
• Problema global de viajes (ciclo de Hamilton)
• Problema de la ruta postal de China

Euler (1707-1783) publicó el primer artículo sobre teoría de grafos en 1736, sentando las bases para algunos teoremas básicos de la teoría de grafos.

Muchos problemas se pueden representar mediante puntos y líneas. Generalmente, los puntos representan entidades y las líneas representan relaciones entre entidades.

Resolver problemas de teoría de grafos con computadoras.

En estudios y exámenes anteriores, la razón por la que podemos calcular los resultados de los problemas de gráficos en poco tiempo es porque la escala de nuestros gráficos no es lo suficientemente grande, por lo que podemos calcularlos a mano. Pero si la escala de esta red es lo suficientemente grande, como la red de carreteras en Suzhou en la siguiente imagen:

Más de 900 nodos y más de 3000 aristas.

Para tal problema, el cálculo manual es casi imposible. Tenemos que depender de las computadoras.

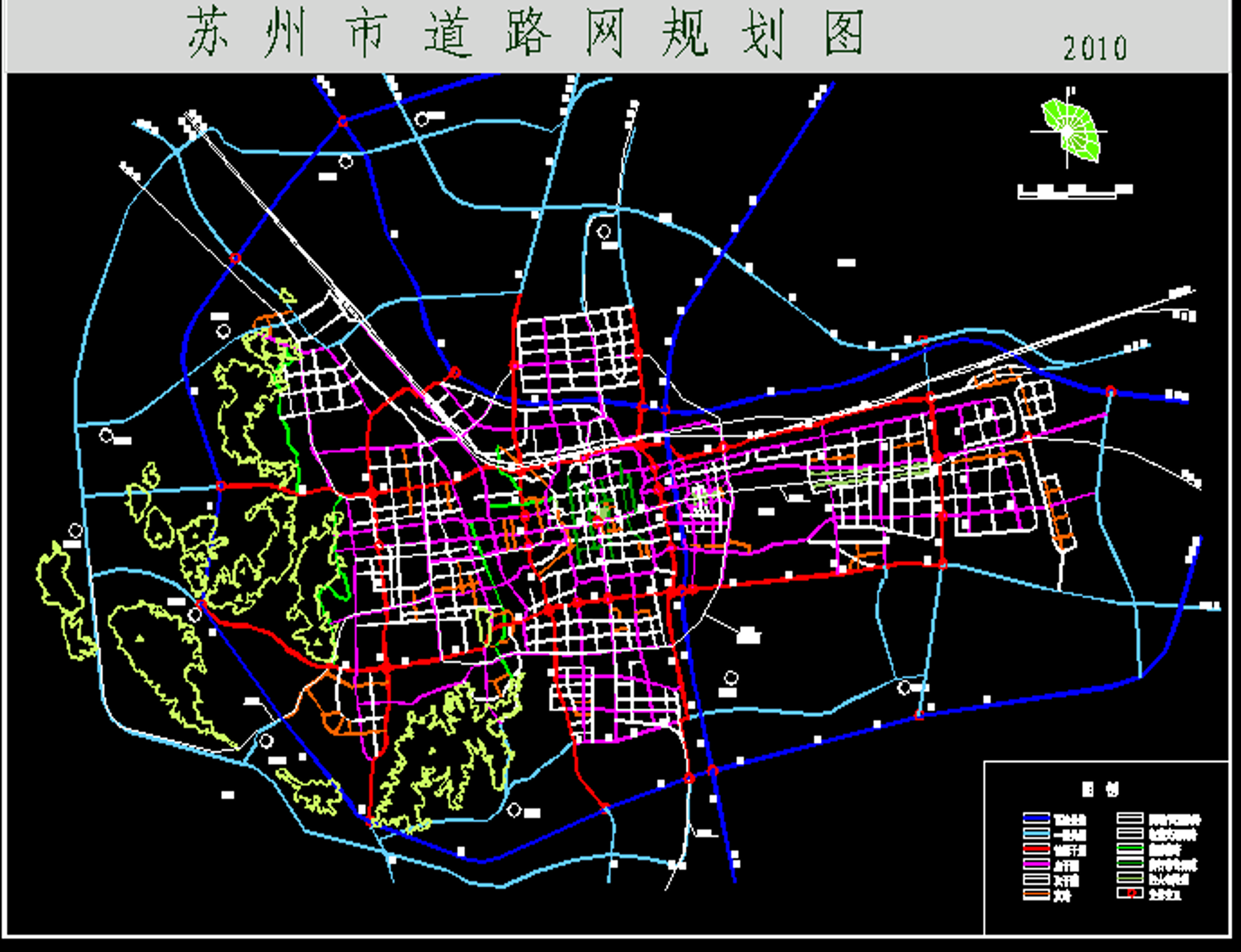
• Una gran cantidad de cálculos de ingeniería no se pueden completar manualmente
• La computación en red en la ingeniería de tráfico debe depender de las computadoras

Una gran cantidad de objetos de ingeniería no se pueden estudiar en objetos reales y solo se pueden abstraer.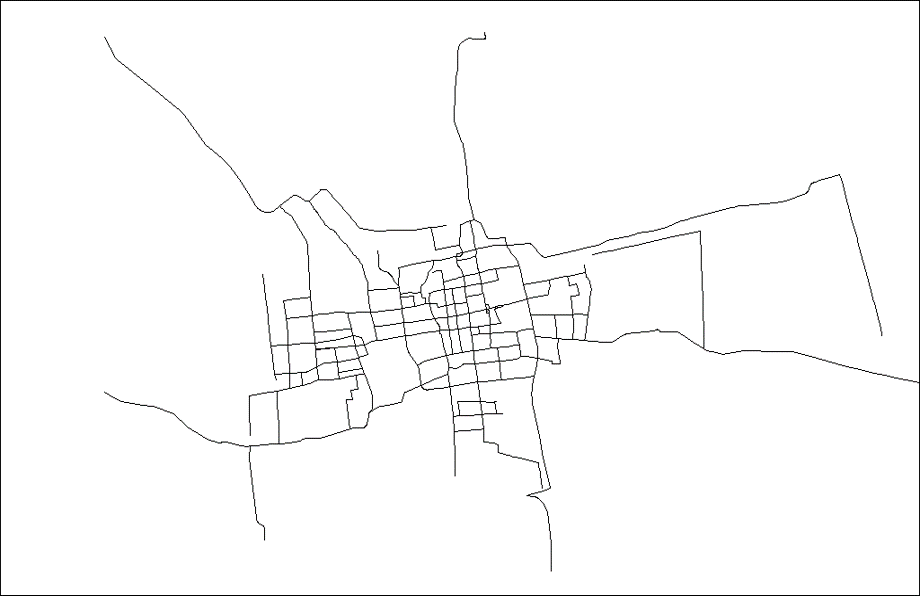

• Red de carreteras, red de líneas de autobuses, etc.

Por ejemplo, para el diagrama de estructura de la red de carreteras de Suzhou anterior, podemos realizar la siguiente abstracción para generar un nuevo diagrama de estructura:

En la imagen también se muestra una sutil red de carreteras, que incluye tanto vehículos de motor como vehículos no motorizados.

En este caso, la escala de los diagramas utilizados en ingeniería de tráfico aumenta geométricamente. Esto refleja aún más la importancia de las computadoras en la resolución de problemas de teoría de grafos.

Descripción general de la teoría de grafos

Hablaremos sobre la teoría de grafos en detalle en otros cursos, por lo que aquí solo la abordaremos brevemente.

Método de expresión de la teoría de grafos en computadoras.

Aquí están las 5 formas más simples.

1. Método de matriz de correlación

Para un gráfico dado, construya la matriz de correlación $A_{a_{yo,}}$,tener:

$$a_{yo,}=\{\begin{array}{l}1,lado{e}_{}con\; el\; punto{V}_{}Asociado\\ 0,\end{array}$$

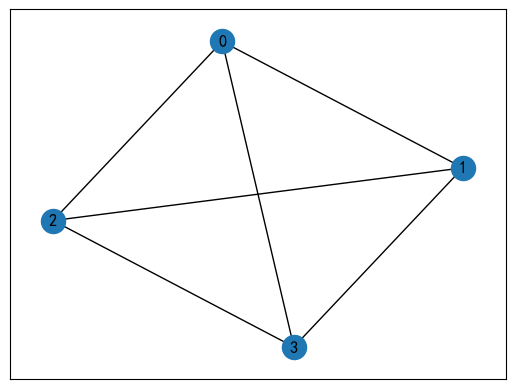
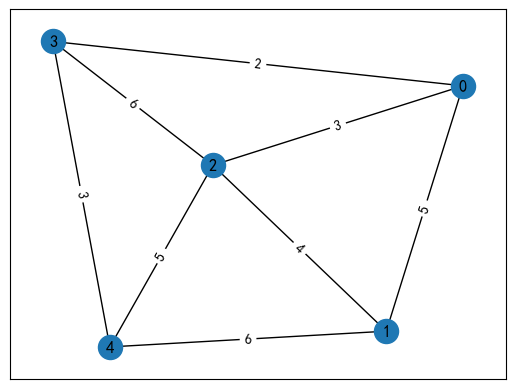
Por ejemplo, para un diagrama de red como este:

Esta figura tiene un total de seis lados y cuatro vértices. La relación entre vértices y aristas se puede expresar como:

nodo/borde	e1	e2	e3	e4	e5	e6
V1	junto a	No adyacente	junto a	junto a	No adyacente	No adyacente
V2	junto a	junto a	No adyacente	No adyacente	junto a	No adyacente
V3	No adyacente	junto a	junto a	No adyacente	No adyacente	junto a
V4	No adyacente	No adyacente	No adyacente	junto a	junto a	junto a

Representado por 0 不接邻y 1 接邻, podemos construir la siguiente matriz de correlación:

$$A=\left[\begin{array}{cccccc}1& 0& 1& 1& 0& 0\\ 1& 1& 0& 0& 1& 0\\ 0& 1& 1& 0& 0& 1\\ & & & & & \end{array}\right]$$

Si desea implementarlo en Python, debe numpyconvertir la matriz de correlación en una matriz de adyacencia. Definimos una función im2ampara implementar esta función:

def im2am( im ):
    import numpy as np
    am = (np.dot( im, im.T) > 0).astype(int)
    np.fill_diagonal(am, 0)
    return am

El principio de este código es el siguiente:

Para la matriz de correlación A, existe la siguiente propiedad: el producto de la matriz de correlación multiplicado por su propia transpuesta es igual a la matriz de adyacencia, pero los elementos diagonales son todos 1 . Ahora mismo:

$$A\times A^t=D_{(Diag=1}$$

Siempre que a los elementos diagonales se les asigne un valor de 0, se puede obtener la matriz de adyacencia.

• np.dot(im, im.T): Este paso consiste en immultiplicar la matriz de correlación con su matriz de transposición para obtener una nueva matriz. Esta operación en realidad calcula el número de conexiones entre cada nodo, es decir, cuántos bordes existen entre los nodos.
• > 0>: Establezca los elementos mayores que cero en la matriz obtenida en el paso anterior en Verdadero mediante el operador de comparación y establezca los elementos menores o iguales a cero en Falso. Esto da como resultado una matriz booleana que indica si existen conexiones entre nodos.
• .astype(int): Convierte una matriz de tipo booleano en una matriz de tipo entero, Verdadero se convierte en 1 y Falso se convierte en 0. De esta forma se obtiene la matriz de adyacencia am.
• np.fill_diagonal(am, 0): Establezca los elementos diagonales de la matriz de adyacencia am(conexiones entre sí mismo y él mismo) en 0. En los diagramas de planificación de redes, normalmente no se considera que los nodos tengan conexiones entre sí.

(Si no sabes qué es una matriz de adyacencia, sigue leyendo, hablaremos de ello a continuación).

im = np.array(
   [ 
      [ 1, 0, 1, 1, 0, 0 ], 
      [ 1, 1, 0, 0, 1, 0 ], 
      [ 0, 1, 1, 0, 0, 1 ], 
      [ 0, 0, 0, 1, 1, 1 ] 
    ] 
  )

# 转换为邻接矩阵
am = im2am( im )
G = nx.from_numpy_array(am)

# 调整图的元素分布位置为放射状分布
# 这样好看
pos = nx.spring_layout(G)

# 绘图
nx.draw_networkx(
  G, 
  pos, 
  with_labels = True
  )

2. Método de matriz de adyacencia

La forma más intuitiva solo representa la relación de adyacencia entre nodos. La lógica de la expresión es la siguiente:

$$d_{yo,}=\{\begin{array}{l}1,El\; nodoiy\; el\; nodojson\; adyacentes\; entre\; sí.\\ 0,\end{array}$$

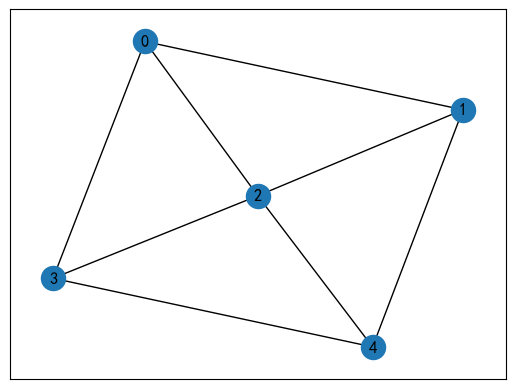
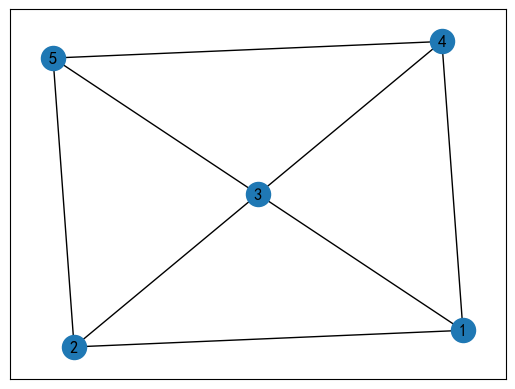
Supongamos que actualmente existe el siguiente diagrama de plan de red:

Podemos escribir una tabla así.

	v1	v2	v3	v4	v5
v1	No adyacente	junto a	junto a	junto a	No adyacente
v2	junto a	No adyacente	junto a	No adyacente	junto a
v3	junto a	junto a	No adyacente	junto a	junto a
v4	junto a	No adyacente	junto a	No adyacente	junto a
v5	No adyacente	junto a	junto a	junto a	No adyacente

Representada por 0 不接邻y 1 接邻, podemos construir la siguiente matriz de adyacencia:

$$D=\left[\begin{array}{ccccc}0& 1& 1& 1& 0\\ 1& 0& 1& 0& 1\\ 1& 1& 0& 1& 1\\ 1& 0& 1& 0& 1\\ & & & & \end{array}\right]$$

adj_mat = np.array(
    [ [ 0, 1, 1, 1, 0 ],
      [ 1, 0, 1, 0, 1 ],
      [ 1, 1, 0, 1, 1 ],
      [ 1, 0, 1, 0, 1 ],
      [ 0, 1, 1, 1, 0 ] ]
  )
G = nx.from_numpy_array(adj_mat)

pos = nx.spring_layout(G)
nx.draw_networkx(G, pos, with_labels = True)

3. Método de matriz de peso

Esta expresión puede expresar el peso de los bordes de cada nodo. La lógica de la expresión es la siguiente:

W ij = { 0 , i = j ∞ , conexión sin bordes wij , i , j conexión de borde W_{ij} = \begin{cases} 0, \ i = j \\ \infty, \ conexión sin bordes\\ w_{ij } , \ i, j conexión de borde\\ \end{cases}W.yo=⎩ ⎨ ⎧0 , i=j∞ , Conexión ilimitadawyo, yo ,j tiene conexión

Del mismo modo, también utilizamos la imagen de arriba como ejemplo. Podemos usar la siguiente tabla para expresar los pesos entre aristas:

(Para nodos que no son adyacentes, usamos $\infty$ para indicar que no hay adyacencia entre dos nodos. )

	v1	v2	v3	v4	v5
v1	0	5	3	2	$\infty$
v2	5	0	4	0	6
v3	3	4	0	6	5
v4	2	$\infty$	6	0	3
v5	$\infty$	6	5	3	0

Asimismo, escribimos la matriz:

$$W_{ij}=\left(\begin{array}{ccccc}0& 5& 3& 2& \infty \\ 5& 0& 4& 0& 6\\ 3& 4& 0& 6& 5\\ 2& \infty & 6& 0& 3\\ \infty & 6& 5& 3& 0\end{array}\right)$$

注意，在 Python 的 NetworkX 中调用 networkx.from_numpy_array() 的时候，$\infty$ 项是表述为 0 的，程序会自动把不同节点之间的 0 识别为 “这条边不存在”，相同节点之间的 0 视作 “自身无环”。不需要设置 float("inf") 或者 np.inf。

但是如果使用 MatLab，就要设置 inf 项。

如果矩阵是从别的什么地方读取的，可以通过下面的设置来替换数据里的 inf：

inf_Index = np.isinf(mat)
mat[inf_Index] = 0

np.isinf() 也可换成 np.isnan() 来替换 NaN 项。

weight_Mat = np.array(
        [
            [ 0, 5, 3, 2, 0 ],
            [ 5, 0, 4, 0, 6 ],
            [ 3, 4, 0, 6, 5 ],
            [ 2, 0, 6, 0, 3 ],
            [ 0, 6, 5, 3, 0 ] 
        ]
    )
G = nx.from_numpy_array(weight_Mat)
pos = nx.spring_layout(G)
nx.draw_networkx(
    G, 
    pos, 
    with_labels = True
    )

# 添加边权绘制的代码
weights = nx.get_edge_attributes(G, "weight")
nx.draw_networkx_edge_labels(
    G, 
    pos, 
    edge_labels = weights,
    font_size = 10
    )

{(0, 1): Text(0.8240830791193997, -0.07520386993244665, '5'),
 (0, 2): Text(0.4262223244243833, 0.3588472968939219, '3'),
 (0, 3): Text(0.059674025608137726, 0.6825840310753251, '2'),
 (1, 2): Text(0.2503054035437831, -0.28291466322645287, '4'),
 (1, 4): Text(0.014103649967479648, -0.7581522828752834, '6'),
 (2, 3): Text(-0.5141036499674789, 0.47487323778131885, '6'),
 (2, 4): Text(-0.38375710472753677, -0.3241011160489147, '5'),
 (3, 4): Text(-0.7503054035437824, -0.0003643818675115873, '3')}

4. 边目录法

把所有出现的边全都用一个目录写出来。

$$\begin{gathered} e_1=(1,2) \\ {e}_2=(2,5) \\ {e}_3=(5,4) \\ {e}_4=(1,4) \\ \cdots \end{gathered}$$

太简单我就不解释了。

在 NetWorkX 里面使用这种方法的时候理论上可以通过字典的设置方法来带上各个边的权重。我这里为了省事就不写了。

G = nx.Graph()
G.add_edges_from(
        [
            [1, 2], [1, 3], [1, 4],
            [2, 3], [2, 5], 
            [3, 4], [3, 5], 
            [4, 5]
        ] 
    )
pos = nx.spring_layout(G)
nx.draw_networkx( G, pos, with_labels = True )

5. 邻接目录法

• 计算机存储效率达到最高，是这里最推荐的方法。

节点号	V(1)：相邻节点数	N(i, j) 相邻节点号
1	2	2, 5
2	3	1, 3, 4
3	2	2, 6
4	3	2, 5, 6
5	3	1, 4, 6
6	3	3, 4, 5

不过这个东西可以不用太关注，只要知道有这么一种形式就好了。我们不是搞计算机专业的，所以大可不用管。因为它不是写给人看的。

换句话说，我拿 Python 演示一下：如果用 networksx.readwrite.adjlist.read_adjlist() 将上面的 G 写入文件

nx.readwrite.adjlist.write_adjlist(
    G,
    "./data/grid.adjlist",
    delimiter = ' ',
    encoding = 'utf-8'
    )

然后我们可以看见文件内是这样的形式：

#D:\Python\Python39\Lib\site-packages\ipykernel_launcher.py --ip=127.0.0.1 --stdin=9003 --control=9001 --hb=9000 --Session.signature_scheme="hmac-sha256" --Session.key=b"db53af50-2b8e-41ac-af10-4983cfca115a" --shell=9002 --transport="tcp" --iopub=9004 --f=c:\Users\asus\AppData\Roaming\jupyter\runtime\kernel-v2-17676oxNCvWsMPa4f.json
# GMT Thu Aug 24 08:40:59 2023
# 
1 2 3 4
2 3 5
3 4 5
4 5
5

这些内容显然不是写给人看的。不过我们还是可以看得出来，这里的信息是从左向右写的，最左边的一列是节点的编号，右边依次排开，用分隔符分开。

象征性地写一下，把上面的表格写入一个 forRead.adjlist：

1 2 5
2 1 3 4
3 2 6
4 2 5 6
5 1 4 6
6 3 4 5

运行下面的代码就能看见图。

G = nx.readwrite.adjlist.read_adjlist(
    "./data/forRead.adjlist",
    delimiter = ' ',
    encoding = 'utf-8'
    )
pos = nx.spring_layout(G)
nx.draw_networkx( G, pos, with_labels = True )

p.s. 这里说一下，就是我尝试过利用 pandas 库的一些功能把上面的 adjlist 储存为 .csv 文件，并且读取为我们熟悉的 DataFrame 二维表的形式，三列分别为节点、与节点邻接的其他节点的数量和邻接目录。但是没有成功。遇到的各种问题我就不多赘述了，反正基本上可以肯定这个东西设计出来就不是给人读的。

一些交通运输上的概念的复习

路段

• 路段是一个边和其两头节点的组合

• 路段是区域交通网络的最基本单元

定义：某种交通运输方式下的某个不受交通工程影响的一个独立的可以进行交通行为的一个边。

路径：是由一个或者很多的路段构成的

运输通道

交通运输通道定义：由起讫点相同，且中途主经由大体相同的绪路径所组成的交通运输带(走廊) 。

运输大通道：在主要客、货流方向上配置有强大交通运输系统的运输通道。

• 一条双向六车道的高速公路
• 一条双线自动闭塞的干线铁路
• 相当的水运通道、管道

通道可能是一个以上的路径并列形成的。

枢纽

是在两条或者两条以上交通线路的交汇、衔接处形成的，具有交通组织、交通中转、交通交换以及部分或者全部交通运输辅助的装卸、仓储、信息服务；及其它辅助服务功能的综合性设施。

我国比较著名的交通枢纽有上海的虹桥，既是机场又是火车、高铁站；还有著名的南京南站。

城市常见的立体交叉口，也属于交通枢纽。

两种典型的网络

1. 点 - 点式网络
2. 轴辐式网络

点 - 点式网络：没有枢纽。

轴辐式网络：分为单枢纽或者多枢纽

相比点 - 点式网络，轴辐式网络的优点在于节约很多不需要开放的线路，可以把流集中到一点。

fig, axes = plt.subplots(
        1, 3,
        figsize = (15,5)
    )

# 点 - 点式网络
Gra_A = nx.Graph()
Gra_A.add_nodes_from([1, 2, 3, 4, 5])
Gra_A.add_edges_from([
    [1, 2], [1, 3], [1, 4], [1, 5],
    [2, 3], [2, 4], [2, 5],
    [3, 4], [3, 5], 
    [4, 5] ]
) 
axes[0].set_title('点 - 点式网络')
nx.draw_networkx( Gra_A, with_labels = True, ax = axes[0] )

# 单枢纽网络式网络
Gra_B = nx.Graph()
Gra_B.add_nodes_from([1, 2, 3, 4, 5])
Gra_B.add_edges_from([
    [1, 5],
    [2, 5],
    [3, 5], 
    [4, 5] ]
) 
axes[1].set_title('单枢纽网络式网络')
nx.draw_networkx( Gra_B, with_labels = True, ax = axes[1] )

# 多枢纽网络式网络
Gra_C = nx.Graph()
Gra_C.add_nodes_from([1, 2, 3, 4, 5, 6, 7, 8])
Gra_C.add_edges_from([
    [1, 4], [2, 4], [3, 4],
    [4, 5], 
    [5, 6], [5, 7], [5, 8], ]
) 
axes[2].set_title('多枢纽网络式网络')
nx.draw_networkx( Gra_C, with_labels = True, ax = axes[2] )

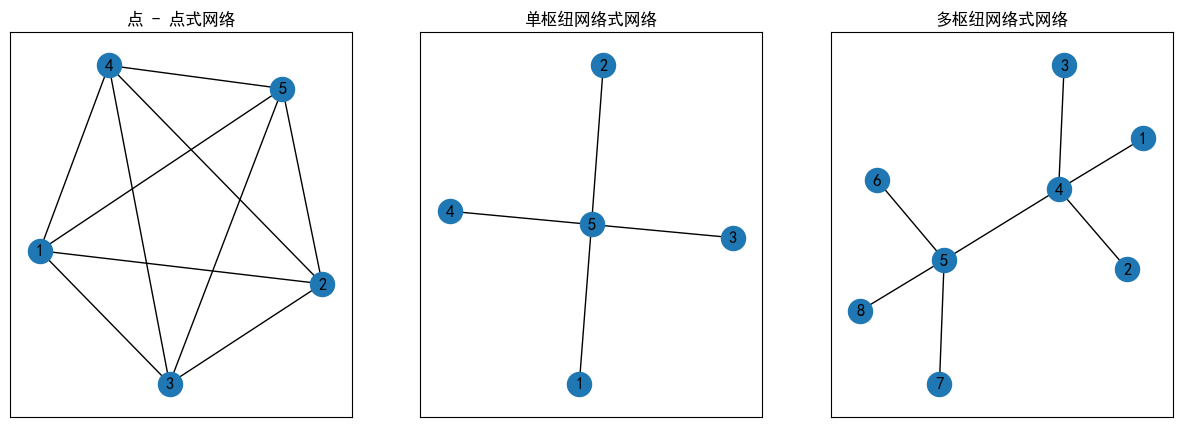
交通网结构

现实的交通运输网的不可避免地要对交通网进行 一定程度的简化、假设和抽象描述

• 详尽的交通网络：即近乎完全按照现实网络进行表示和绘制，内容全，但可能表示和分析较为困难。对于宏观网络或者小区域网络适用。
• 逻辑网络：对实际网络进行功能性、或者结构关系的简化，得到抽象逻辑性网络，其中的节点和边主要代表交通逻辑关系。
  • 功能性、可达性网络：属于逻辑网络的一种，用于对区域部分性能的分析。
• 结构网络：仅仅模拟区域交通的结构，进行辅助性的管理使用。
• 参数网络：仅仅对主要参数进行抽取，一般更适用于规划或者管理方面。

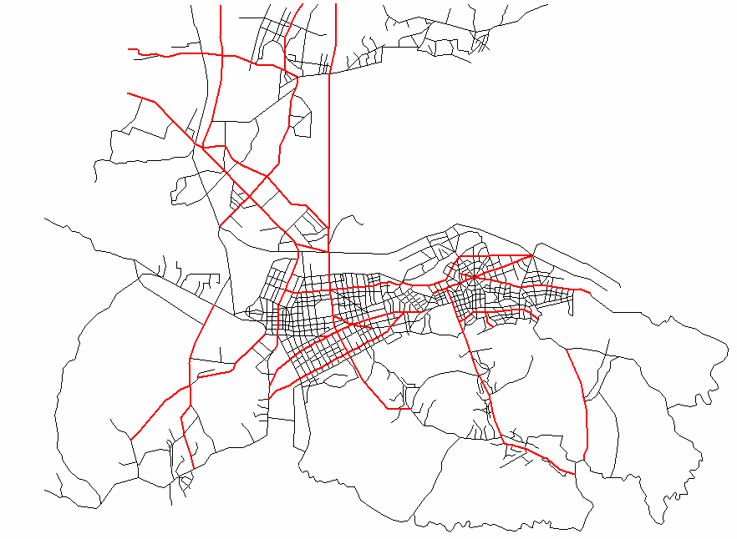
下图展示了经过简化的大连主干道路网。这个图是用 MapInfo 画的。

复杂网络理论及其应用

我们学校很多教授都在搞这个，写了很多质量很高的 SCI 论文。

• 小世界实验：六度分离、Erdos数、bacon数等
• 一些实际的复杂网络系统：Web、科学家合作网络、经济网络、交通网络、疾病传播等
• 复杂网络的静态几何量：度分布、聚类系数、平均路径长度等
• 网络拓扑的基本模型及其性质：随机网络、Small World网络、Scale Free网络等

近几年的研究态势：发展历程、会议、论文、软件、实证等

六度分离

我们会不会有这样的经历：半夜看朋友圈的时候，发现自己的室友给自己的小学同学点了个赞。一问才发现几年前两个人参加了某个活动，早就认识了。感叹世界多么小！

我们或许有过这样的经历：偶尔碰到一个陌生人，同他聊了一会后发现你认识的某个人居然他也认识，然后一起发出 “这个世界真小” 的感叹。那么对于世界上任意两个人来说，借助第三者、第四者这样的间接关系来建立起他们两人的联系平均来说最少要通过多少人呢？

美国社会心理学家斯坦利•米尔格伦(Stanley Milgram)在1967年通过一些实验后得出结论：中间的联系人平均只需要5个。他把这个结论称为 “六度分离” (six degrees of separation)。

六度分离: 平均只要通过5个人，你就能与世界任何一个角落的任何一个人发生联系。这个结论定量地说明了我们世界的”大小”，或者说人与人关系的紧密程度。

30多年来，六度分离理论一直被作为社会心理学的经典范例之一。

尽管如此，实际上这个理论并没有得到严格的证实。美国心理学教授朱迪斯•克兰菲尔德(Judith Kleinfeld)对米尔格伦最初的实验提出不同意见，因为她发现实验的完成率极低。

实验的步骤：

1. 首先把志愿者交给 A，告诉他要把信件送给 S
2. 如果他不认识 S，可以先把信件交给他认识的朋友 B，B 是他认为最可能认识 S 的人
3. B 把信件转递给其他人
4. 如果统计样本中的多个 A 到 S 只有 6 次传递，那么结论成立。

然而，在这个实验中，实际上只有三分之一的信送到了收信人那里，因此实验的完成率很低。

但是试验数据表明世界确实比我们想象的要小！

小世界实验

Paul Erdos ( (1913-1996)， 出生于匈牙利的犹太籍数学家，被公认为本世纪最伟大的天才之一。

Erdos毕生发表的论文超过1500篇（在数学史上仅次于欧拉 (Euler ，1707-1783) )，超长的合作者名单,合作者超过450位。但若加上别人所做，但曾获他关键性的提示之论文，则他的论文应有数万篇。

他的研究领域主要是数论和组合数学，但他的论文中涵盖的学科有逼近论、初等几何、集合论、概率论、数理逻辑、格与序代数结构、线性代数、群论、拓扑群、多项式、测度论、单复变函数、差分方程与函数方程、数列、Fourier 分析、泛函分析、一般拓扑和代数拓扑、统计、数值分析、计算机科学、信息论等等。

“Mathematical Reviews” 曾把数学划分为大约六十个分支，Erdos的论文涉及到了其中的 40%.

数学家以下述方式来定义 Erdos 数 (Erdos number) : Erdos 本人之 Erdos 数为 0，任何人若曾与 Erdos 合写过论文，则其 Erdos 数为 1。任何人若曾与一位 Erdos 数为 l (且不曾与有更少的 Erdos 数) 的人合写过论文， 则他的 Erdos 数为 2

几乎每一个当代数学家都有一个有限的 Erdos 数，而且这个数往往非常小，小得出乎本人的预料。比如说证明 Fermat 大定理的 Andrew Wiles，他的研究方向与 Erdos 相去甚远，但他的 Erdos 数只有 3，是通过这个途径实现的：

• Fields 奖得主的 Erdos 数都不超过 5,（只有 Cohen 和 Grothendieck 的 Erdos 数是 5）
• Nevanlinna 奖得主的 Erdos 数不超过 3，（只有 Valiant 的 Erdos 数是 3）
• Wolf 数学奖得主的 Erdos 数不超过 6，（只有 V.I.Arnold 是 6，且只有 Kolmogorov 是 5，）
• Steele 奖的终身成就奖得主的 Erdos 数不超过 4.

在具有有限 Erdos 数的人名单中往往还能发现一些其他领域的专家，如: 比尔盖兹(Bill Gates)， 他的 Erdos 数是4，通过如下途径实现：

爱因斯坦是2.

Kavin Bacon

贝肯数来源于一个好莱坞游戏，这个游戏要求参与者们尝试用各种方法，把某个演员和凯文·贝肯这个美国好莱坞演员有联系，并且尽可能减少中间的环节。

想方设法把好莱坞的每个演员用最多六步把他们的娱乐圈关系与演员凯文贝肯联系起来。当作为一个游戏，玩家必须尽量以最少的步骤连接男女演员和凯文贝肯关系。男女演员的贝肯数是他们与凯文贝肯来往关系程度。某个演员他或她的数字越大，那么他们离凯文的关系和来往就越远。

凯文在比赛中得了 0 名。一个在电影里和他一起工作的演员会有第一名。如果一个演员和另一个演员直接与凯文合作过的演员合作，他就会排在第二名，以此类推。只有12%的演员无法定义数字，如果得出这样的结果就说明他们无法任何方式与凯文联系在一起。

凯文贝肯起初并不喜欢这个游戏，但后来他发现有那么多娱乐圈的演员可以和他联系在一起，他觉得不可思议。凯文贝肯曾出演过许多电影，并与许多著名演员合作过。一个演员的本肯数越小那他们就可以有多出名。此外，与凯文一起编导电影的编剧，作家和工作人员的其他人也可以使用贝肯数，凯文他出演过许多好莱坞的好电影里，所以一个演员的贝肯数越小，他就越出名。

发现: 在曾经参演的美国电影演员中，没有一个人的 Bacon 数超过 4

在网上有一个网页 The Oracle of Bacon。网站的数据库里总共存有有 783940 个世界各地的演员的信息以及 231, 088 部电影信息。

通过简单地输入演员名字就可以知道这个演员的 bacon 数。

目前比如输入 Stephen Chow（周星驰）就可以得到这样的结果：周星驰在 1991 (Haomen yeyan) 》 中与洪金宝 (Sammo Hung Kam-Bo) 合作；而洪金宝又在李小龙的最后一部电影，即 1978 年的《死亡的游戏 （Game of Death）》 中与 Colleen Camp 合作；Colleen Camp 在去年的电影《Trapped》 中与 Kevin Bacon 合作。这样周星驰的培根数为 3。

对所有这将近 78 万个演员所做的统计。结果如下所示: 左边是 Bacon 数，右边是拥有这个 Bacon 数的演员个数。可以看到最大的培根数仅仅为 8。平均培根数仅为 2.948。

Kevin Bacon Number	# of prople
0	1
1	1962
2	171652
3	485636
4	115701
5	8124
6	779
7	72
8	13

Kavin Bacon图

• 有明确的定义（顶点和边）
• 数据库中 90% 的演员被归入到一个单独的连通分支
• 最高的有限 Bacon 数为 8

平均 Bacon 数为 2.9

注：少数演员承担了将多数演员联系在一起的工作。

Estos contenidos reflejan la importante naturaleza universal de la red, es decir, ¡ la función de conexión a menudo solo la desempeñan unos pocos nodos!

red

Una red es un sistema que incluye una gran cantidad de individuos e interacciones entre individuos.

Cualquier red se puede resumir en un gráfico (se remonta a la investigación de Euler sobre el problema de los siete puentes de Konogsberg).

Propiedades topológicas de la red: propiedades de la red que no dependen de las posiciones específicas de los nodos ni de las formas específicas de los bordes.

Clasificación de gráficos: gráfico no dirigido, gráfico dirigido, gráfico ponderado, gráfico mixto

Un gráfico simple se refiere a un gráfico sin dirección, sin peso, sin aristas duplicadas y sin bucles automáticos.

Actualmente, existen muchos resultados de investigación sobre redes simples.

En este curso sólo nos ocuparemos de gráficos simples.