Prueba y código fuente del cálculo de la distancia desde el vértice espacial al plano

Propósito: Recientemente escribí código C++ y encontré algunos algoritmos básicos. Como calcular la distancia de un vértice a un plano.

El artículo anterior ha introducido el plano y su expresión matemática:
expresión geométrica $PAGS l a n mi$ : plano normal vector $N=\begin{pmatrix} n_0 \\ n_1 \\ n_2 \end{pmatrix}$ , y un vértice $P_0=\begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix}$
Expresión de vértice: $P_1=\begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix}$

Calcular $P_1$ Al plano $Distancia del plano$ . $_$ $_$ $_$
$La expresión de P l a n e$ se puede transformar en $n_0(x-x_0)+n_1(y -y_0 )+n_2(z-z_0)=0$ , calcular $n_0x+n_1y+n_2z+d=0$ 其中 $d=-n_0x_0-n_1y_0-n_2z_0=-N^T \cdot P_0$

La fórmula de derivación es la siguiente:
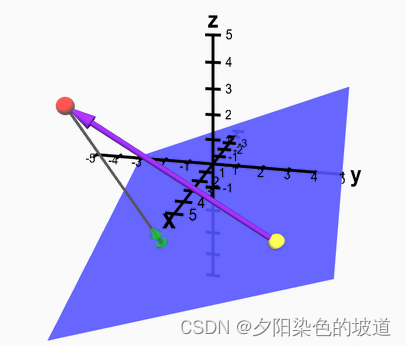
inserte la descripción de la imagen aquí

Calcular el vértice rojo $P_1$ Al avión azul $Distancia del plano$ . $_$ $_$ $_$ $P_0$ en el plano $PAG$ . Definición de distancia de vértice a plano: la distancia de su punto perpendicular al plano (indicado por el segmento de línea gris en la figura).

Según el algoritmo del triángulo vertical, la longitud del segmento de la línea gris es $re yo s t$
$dist=\lVert P_0-P_1 \rVert \cdot cos(\theta) \space \space (1)$
aumentar $\theta$ son dos vectores $P_0P_1$ y plano vector normal $Por ejemplo$ ,
$cos(\theta) = \cfrac {|N^T \cdot (P_0 -P_1)|}{\lVert P_0-P_1 \rVert \cdot \lVert N \rVert} \space \space(2)$
Sustituyendo la fórmula (2) en la fórmula (1) se puede obtener de la siguiente manera:
$dist=\cfrac {|N^T \cdot ( P_0 -P_1)|}{ \lVert N \rVert} \espacio \espacio (3)$
Pon el vector $P_0=\begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix}$ , $P_1=\begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix}$ , $\begin{pmatrix} n_0 \\ n_1 \\ n_2 \end{pmatrix}$ La ecuación
$dist=\cfrac {|N^T \cdot P_0 - N^T \cdot P_1|}{ \lVert N \rVert}=\cfrac {|-d - N^T \cdot P_1|}{ \lVert N \rVert} =\cfrac {|N^T \cdot P_1 + d|}{ \lVert N \rVert} \space \space (4)$

La forma vectorial anterior se puede reescribir en forma algebraica:
$\cfrac {|n_0x_1 + n_1y_1+n_2z_1+d|}{\sqrt{n_0^2+n_1^2+n_2^2}} \espacio \espacio (5)$

El código fuente es el siguiente, está escrito en modo vectorial. Requiere que configure la biblioteca Eigen:

float Pnt3d2PlaneDist(Eigen::Vector4f& fn, Eigen::Vector3f& pnt)
	{
    
    
		Eigen::Vector3f n = Eigen::Vector3f(fn[0], fn[1], fn[2]);
		float sd = n.norm();
		if (sd < 1e-8)
			return std::numeric_limits<float>::max();
		float sb = std::abs(n.dot(pnt) + fn[3]);
		float d = sb / sd;
		return d;
	}

Consulte el sitio web para obtener más detalles: https://mathinsight.org/distance_point_plane

Prueba y código fuente del cálculo de la distancia desde el vértice espacial al plano

Supongo que te gusta