Diseño y análisis de algoritmos Resumen final

0000 Prefacio: es básicamente para mí leer algunas cosas que tiendo a olvidar, para prepararme para el examen, principalmente para la segunda mitad del conocimiento, para la primera mitad, consulte el resumen del examen de la etapa de diseño y análisis del algoritmo .

capítulo cinco

Un algoritmo de backtracking es un método de búsqueda sistemática de una solución a un problema. Todas las soluciones posibles de un problema se denominan el espacio de solución del problema.Si el espacio de solución es limitado, el espacio de solución se puede mapear en una estructura de árbol . La idea básica del algoritmo de backtracking es: avanza desde un camino, avanza si puedes, retrocede si no puedes e intenta otro camino.

Conceptos relacionados 1

• nodo de extensión
• Nodo deslizante
• nodo muerto

Conceptos relacionados 2

• Árbol de subconjuntos: se requiere tiempo de cálculo O(2n) para atravesar el árbol de subconjuntos
• Árbol de permutación: se requiere tiempo de cálculo O(n!) para recorrer el árbol de permutación

Capítulo Seis

El método de bifurcación y acotación es un algoritmo para resolver problemas de optimización, por lo general busca en el árbol espacial de solución del problema primero en amplitud o primero en costo mínimo (beneficio máximo). La idea básica es expandir las soluciones factibles del problema y luego encontrar la mejor solución de cada rama .

En el método de bifurcación y límite, la bifurcación debe usar la estrategia de ancho primero para generar todas las bifurcaciones del nodo extendido a su vez. El límite es calcular el límite superior del nodo durante el proceso de expansión del nodo y cortar algunas ramas durante la búsqueda.

Diferencia de retroceso

Los objetivos de la solución son diferentes.

• El método de retroceso consiste en encontrar todas las soluciones que satisfagan las restricciones
• El método de ramificación y acotación consiste en encontrar una solución que satisfaga las condiciones, o la solución óptima en cierto sentido

buscar de manera diferente

• Retrocediendo: profundidad primero
• Método de ramificación y límite: primero la amplitud o primero el menor costo

Conceptos relacionados

• Nodo deslizante
• tabla de nodos en vivo PT
• nodo de extensión
• nodo hijo
• rama en cola y enlazada
• rama de cola de prioridad y límite

Capítulo VII

Los algoritmos de aleatorización se dividen en cuatro categorías:

• Algoritmo de aleatorización numérica
• Algoritmo de Montecarlo
• Algoritmo de Las Vegas
• Algoritmo de Sherwood

Entrada al algoritmo de aleatorización

• entrada al problema original
• Una secuencia de números aleatorios elegidos al azar

Los algoritmos estocásticos numéricos se utilizan a menudo para resolver problemas numéricos. Estos algoritmos a menudo obtienen soluciones aproximadas, y la precisión de las soluciones aproximadas aumenta con el aumento del tiempo de cálculo. En muchos casos, es imposible o innecesario calcular la solución exacta del problema, y ​​se puede utilizar el algoritmo numérico de la base imponible para obtener una solución bastante satisfactoria.

Los problemas numéricos se usan comúnmente en varios cálculos matemáticos integrales y diferenciales.

El algoritmo de Monte Carlo se utiliza para encontrar la solución exacta del problema. Para muchos problemas, las soluciones aproximadas no tienen sentido. Se puede encontrar una solución al problema con el algoritmo de Monte Carlo, pero la solución puede no ser correcta. La probabilidad de encontrar la solución correcta depende del tiempo que tarde el algoritmo. Cuanto más tiempo tome el algoritmo, mayor será la probabilidad de obtener la solución correcta. La principal desventaja del algoritmo Monte Carlo también está aquí. En general, es imposible juzgar efectivamente si la solución obtenida es determinable y correcta. (¡Los casos no generales pueden ser juzgados!)

El algoritmo de Las Vegas no obtiene soluciones incorrectas. Una vez que se encuentra una solución usando el algoritmo de Las Vegas, debe ser la solución correcta. Pero a veces el algoritmo de Las Vegas no puede encontrar una solución. La probabilidad de que el algoritmo de Las Vegas encuentre la solución correcta aumenta a medida que aumenta el tiempo de cálculo que tarda.

El algoritmo de Sherwood  siempre puede encontrar una solución correcta al problema, eliminar la correlación entre el peor de los casos de comportamiento del algoritmo y una instancia específica no mejora el desempeño promedio, ni evita deliberadamente el peor de los casos de comportamiento del algoritmo.

Precauciones

• No se puede garantizar que el resultado del algoritmo de aleatorización sea correcto, pero su probabilidad de error puede ser limitada;
• El algoritmo de aleatorización puede tener diferentes resultados para la misma instancia de entrada en diferentes ejecuciones, por lo que el tiempo de ejecución del algoritmo de aleatorización puede ser diferente para la misma instancia de entrada.

Análisis de Algoritmos

retrocediendo

Programación de trabajos por lotes (suposición)

Dado un conjunto de n trabajos {J1,J2,...,Jn}. Cada trabajo debe ser procesado primero por la máquina 1 y luego por la máquina 2. El trabajo Ji requiere un tiempo de procesamiento tij en la máquina j. Para un cronograma de trabajo definido, sea Fij el momento en que el trabajo i completa el procesamiento en la máquina j. La suma de los tiempos de procesamiento de todos los trabajos en la máquina 2 se denomina suma de los tiempos de finalización del cronograma del trabajo. El problema de programación de trabajos por lotes requiere que, para n trabajos dados, se formule el mejor esquema de programación de trabajos para minimizar la suma del tiempo de finalización.

Preguntas después de N (omitido)

Coloque n reinas que no sean atacadas entre sí en un tablero de cuadrícula de n × n. De acuerdo con las reglas del ajedrez, una reina puede atacar una pieza que esté en la misma fila o columna o en la misma diagonal que la reina. El problema de las n reinas es equivalente a colocar n reinas en una cuadrícula de n × n, y dos reinas cualesquiera no se colocan en la misma fila o columna o en la misma barra inclinada. El problema tiene solución si y solo si n = 1 o n ≥ 4.

tren de pensamiento

Cuatro soluciones posteriores al problema

Problema del triángulo simbólico (omitido)

 tren de pensamiento

Utilice la n-tupla x[1:n] para representar los n símbolos de la primera fila del símbolo triángulo. Cuando x[i] es igual a 1, significa que el i-ésimo símbolo de la primera fila del símbolo triángulo es "+"; cuando x Cuando [i] es igual a 0, significa que el i-ésimo símbolo en la primera fila del símbolo triángulo es "-"; 1<=i<=n. Dado que x[i] tiene 2 valores. Por lo tanto, cuando se usa el método de retroceso para resolver el problema del triángulo simbólico, se puede usar un árbol binario completo para representar su espacio de solución. Después de determinar los primeros i símbolos x[1:i] en la primera fila del triángulo de símbolos, se determina un triángulo de símbolos que consta de i*(i+1)/2 símbolos.

(i*(i+1)/2 proviene de la fórmula de suma de la secuencia aritmética cuyo primer elemento es 1 y la tolerancia es 1)

 Juicio irresoluble: n*(n+1)/2 es un número impar

0-1 problema de mochila

 Ejercicio: Un ejemplo del problema de la mochila 0-1 es: n=4, c=16, p=[22,21,16,7], w=[11,10,8,7]. Para resolver este problema de acuerdo con el método de retroceso, intente responder las siguientes preguntas:

(1) ¿Cuál es la función de restricción para este problema?

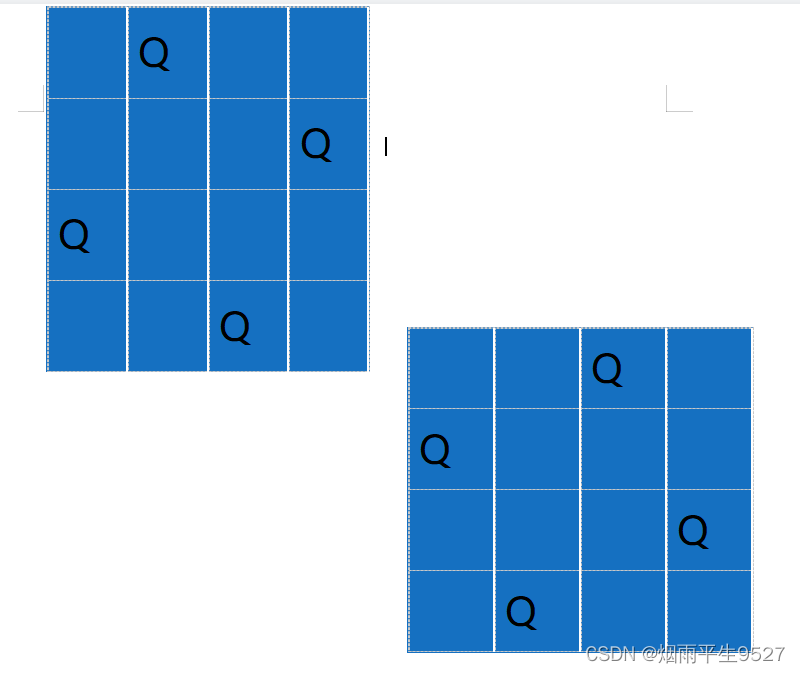
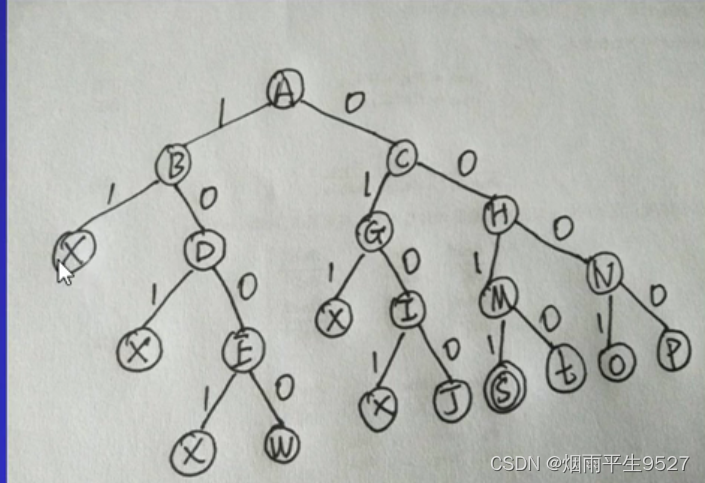
(2) Dibuje el árbol del espacio de soluciones para encontrar la solución óptima. Los nodos que deben descartarse en el medio (soluciones que no cumplen las condiciones de restricción) se marcan con ×, los nodos que obtienen soluciones intermedias se enmarcan con un solo círculo ○ y la solución óptima se enmarca con un doble círculo ◎.

Respuesta: (1) La función de restricción es: ∑wixi≤C, es decir, la mochila puede contener artículos

(2) El árbol del espacio de soluciones se muestra en la siguiente figura.

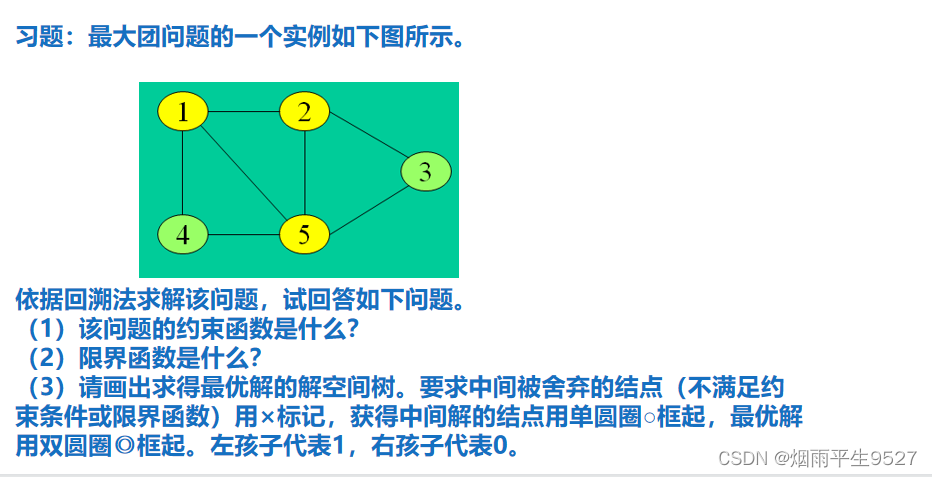
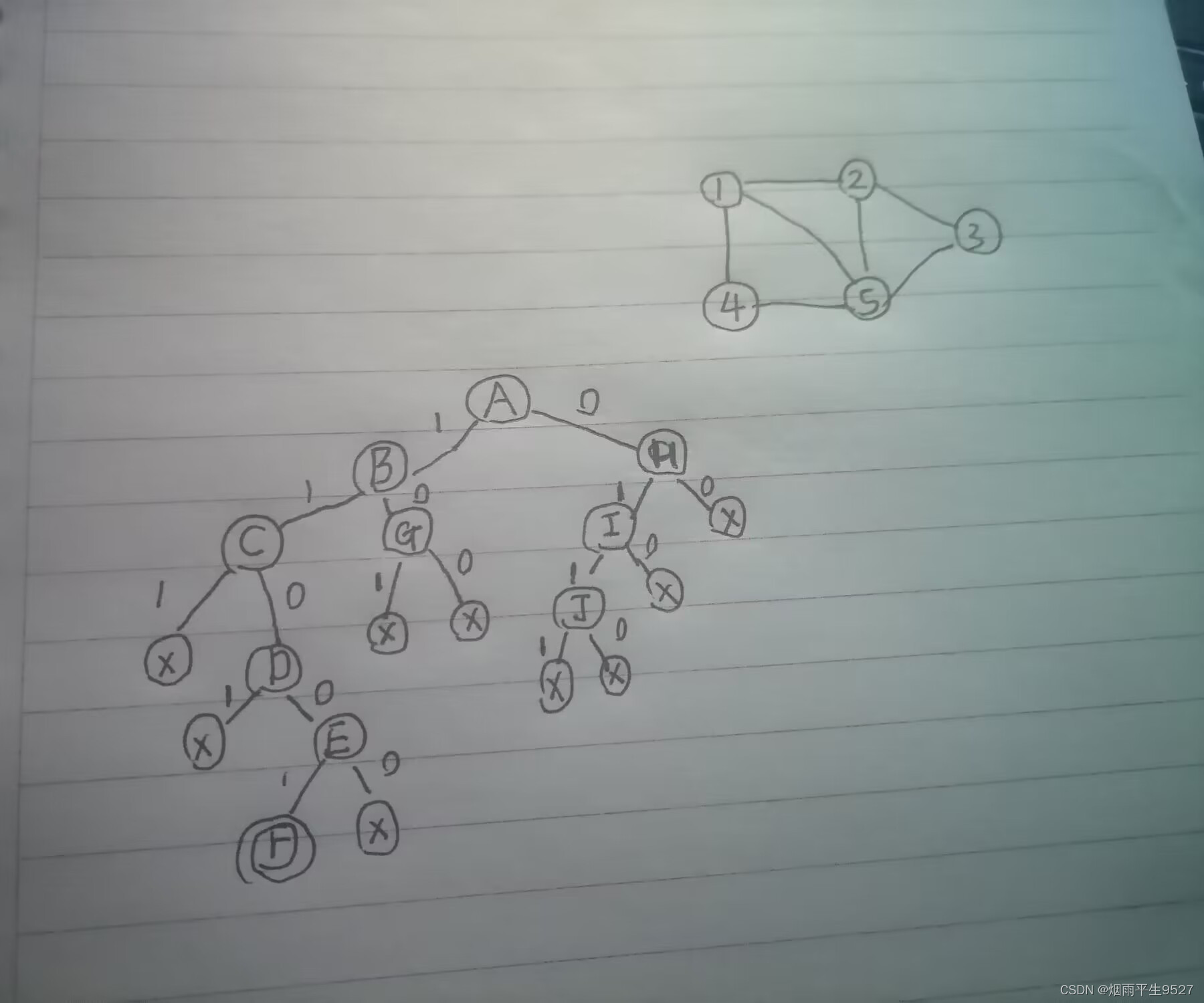
Ejercicios de grupo más grande (suposición)

 Función de restricción de factibilidad: cada vértice desde el vértice actual hasta el conjunto de vértices seleccionado está conectado por un borde.

(2) Función de límite: hay suficientes vértices opcionales para que el algoritmo pueda encontrar una camarilla más grande en el subárbol derecho.

rama y atado

0-1 problema de mochila

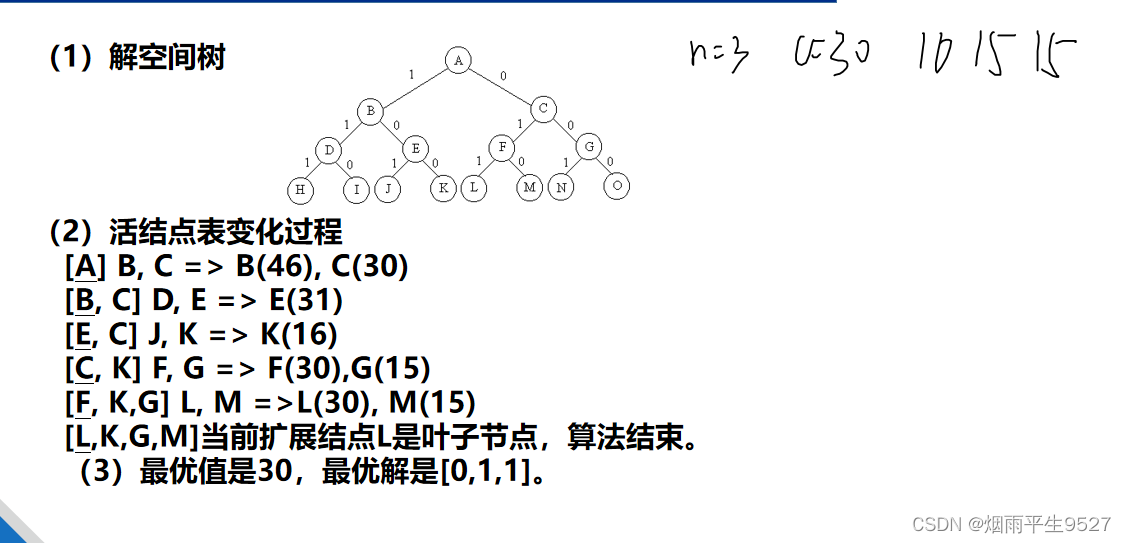
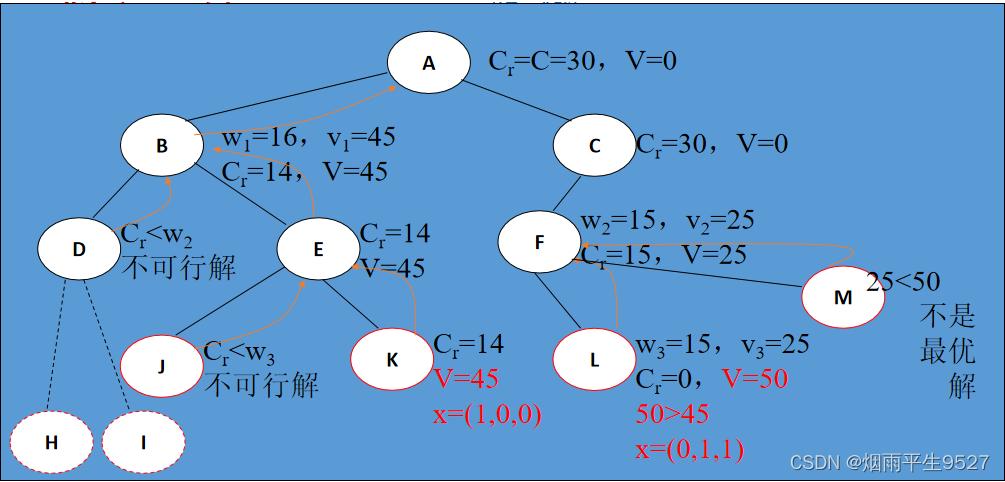
Considere la siguiente instancia del problema de la mochila 0-1: n=3, c=30, w=[16,15,15], v=[45,25,25]

rama y atado

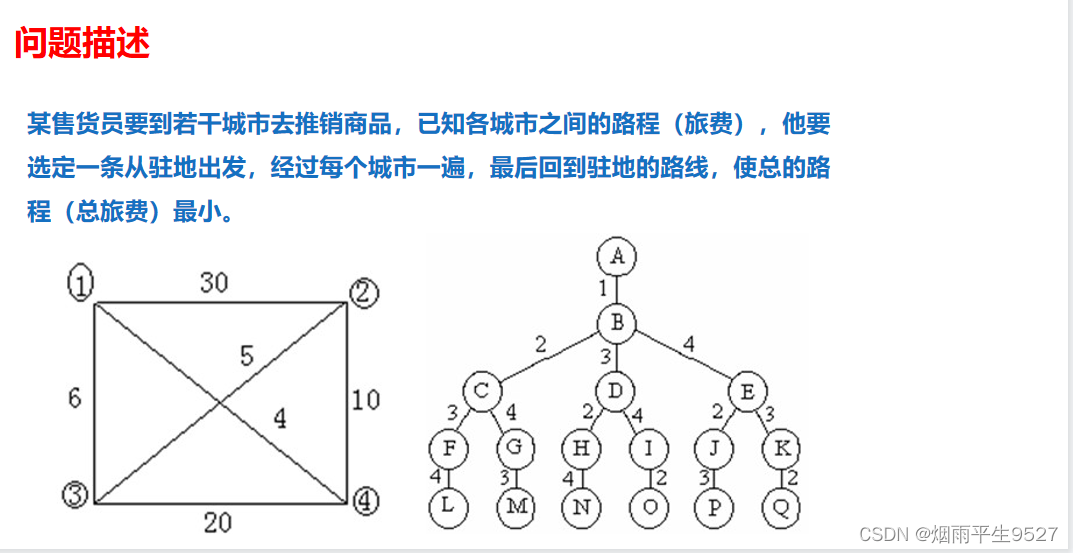
Problema del viajante de comercio (la misma idea solo se pone en PPT) (omitido)

rama en cola y enlazada

rama de cola de prioridad y límite

El problema de carga es el mismo.

rama en cola y enlazada

Rama de cola de prioridad y método enlazado (suposición)

Cuando se da el método de ramificación y enlace de la cola de prioridad para resolver este ejemplo, el proceso de cambio de la tabla de nodos en vivo (la prioridad es la suma del peso del contenedor en el barco actual más el peso del contenedor restante). Método de descripción: [A,B,C]FGF(40), donde [A,B,C] es la tabla de nodos activos, A es el nodo expandido actual, A genera FG y G no cumple con los restricciones y está cortado, 40 significa la prioridad del nodo F 

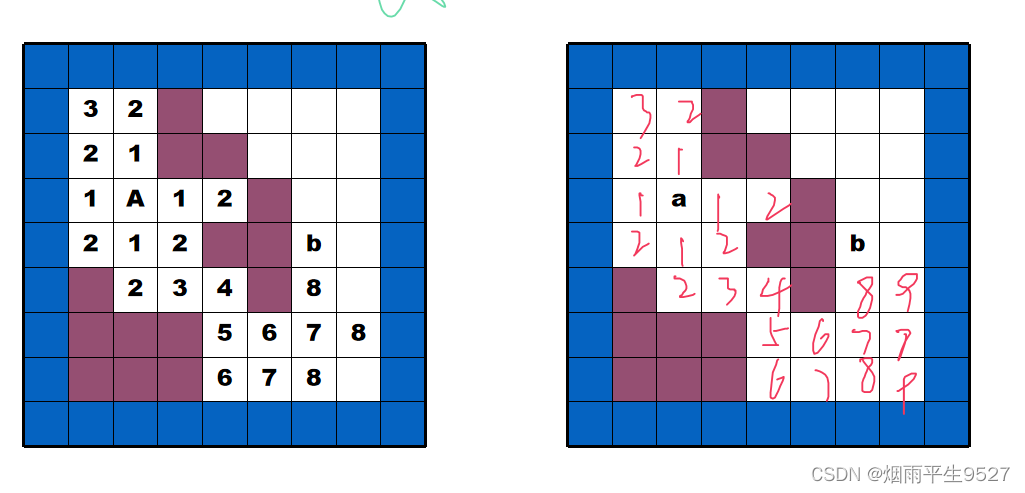
Ejemplos de problemas de cableado

algoritmo de aleatorización

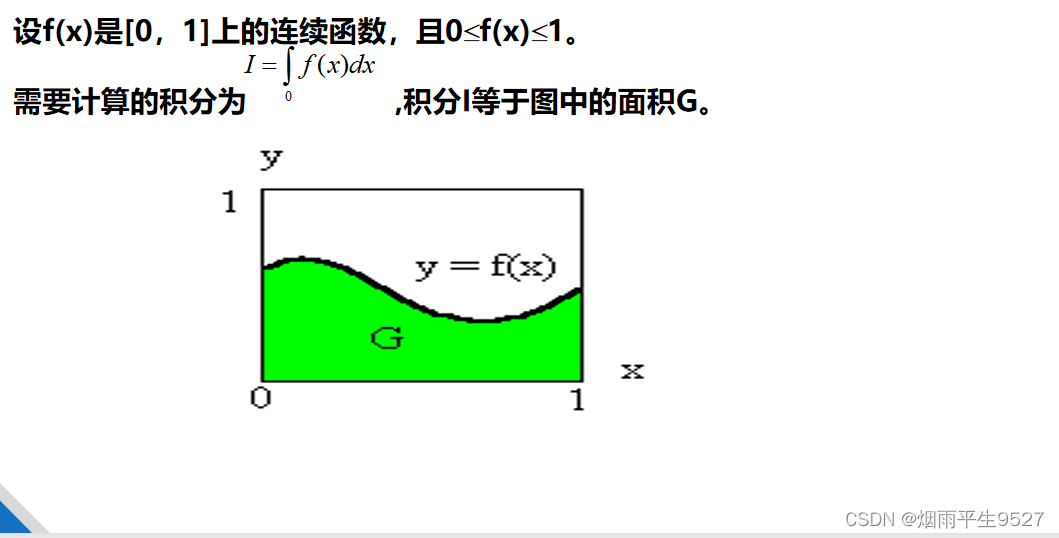
 Cálculo de la integral definida por el método del punto de conversión de números aleatorios

Algoritmo de aleatorización Monte Carlo

programación

retrocediendo

problema de carga

Descripción del problema

Hay un lote de n contenedores para ser cargado en 2 barcos con cargas C1 y C2 respectivamente, donde el peso del contenedor i es wi, y ∑wi ≤ C1+C2 El problema de carga requiere determinar si existe un esquema de carga razonable que pueda cargar esto Los contenedores fueron cargados en los 2 barcos. Si es así, encuentre un esquema de carga. Es fácil probar que si un problema de carga dado tiene solución, el esquema de carga óptimo puede obtenerse adoptando la siguiente estrategia: (1) Primero, llene el primer barco lo más lleno posible; (2) Cargue los contenedores restantes en el segundo barco barco.

análisis del problema

clave

// 搜索到叶子节点
    if (i > n) {
        // 如果找到更优解，则更新最优解
        if (cw > bestw) {
            bestw = cw;
            for (int j = 1; j <= n; j++) {
 
                best[j] = x[j];
            }
        }
        return;
    }
    // 搜索左子树
    r -= w[i];
    if (cw + w[i] <= c) {
        x[i] = 1;
        cw += w[i];
        backtrack(i + 1);
        cw -= w[i];
    }
    r += w[i];
    // 搜索右子树
    if (cw + r > bestw) {
        x[i] = 0;
        backtrack(i + 1);
    }

código detallado

#include <stdio.h>
#define MAX_N 20
 
int n;                      // 货物数量
int c;                      // 车的载重量
int w[MAX_N],x[MAX_N];               // 每个货物的重量
int best[MAX_N];            // 最优解
int cw;                     // 当前载重量
int bestw;                  // 最优载重量
int r;                      // 剩余物品重量和
 
// 搜索装载方案
void backtrack(int i)
{
    // 搜索到叶子节点
    if (i > n) {
        // 如果找到更优解，则更新最优解
        if (cw > bestw) {
            bestw = cw;
            for (int j = 1; j <= n; j++) {
 
                best[j] = x[j];
            }
        }
        return;
    }
    // 搜索左子树
    r -= w[i];
    if (cw + w[i] <= c) {
        x[i] = 1;
        cw += w[i];
        backtrack(i + 1);
        cw -= w[i];
    }
    r += w[i];
    // 搜索右子树
    if (cw + r > bestw) {
        x[i] = 0;
        backtrack(i + 1);
    }
}
 
int main()
{
    //printf("请输入货物数量和车的载重量（用空格分隔）：\n");
    scanf("%d%d", &n, &c);
    //printf("请输入每个货物的重量：\n");
    for (int i = 1; i <= n; i++) {
        scanf("%d", &w[i]);
        r += w[i];
    }
    backtrack(1);
    printf("最优装载方案为：\n");
    for (int i = 1; i <= n; i++) {
        if (best[i]) {
            printf("%d ", i);
        }
    }
    printf("\n最优载重量为：%d\n", bestw);
    return 0;
}

0-1 Mochila ( El PPT es feo y acuoso, recomendado para el examen · el siguiente código)

Código PPT, consulte el blog Experimento de diseño de algoritmo de retroceso

donde esta el codigo de la llave

int bound(int t)
{
    int cleft = C - CurWeight;//剩余容量
    int b = CurValue;//现阶段背包内物品的价值
    while (t <= n && w[t] <= cleft)//以物品重量价值递减装入物品
    {
        cleft = cleft - w[t];
        b = b + v[t];
        t++;
    }
    if (t <= n)//装满背包
        b = b + v[t] * cleft / w[t];//计算t号物品的单位价值装满剩余空间
    return b;
}
void backtrack(int t)
{
    if (t > n)//到达叶子节点了
    {
        if (CurValue > BestValue)//已经搜寻完一次了，把现有的最大值赋值；
        {
            BestValue = CurValue;
            for (int i = 1; i <= n; i++)
                BestX[i] = X[i];
        }
        return;
    }
    if (CurWeight + w[t] <= C)//不到背包最大容量进入左子树
    {
        X[t] = 1;//记录是否装入
        CurWeight += w[t];
        CurValue += v[t];
        backtrack(t + 1);//回溯
        CurWeight -= w[t];
        CurValue -= v[t];
    }
    if (bound(t + 1) > BestValue)//进入右子树
    {
        X[t] = 0;//他自己没有后面物品合适
        backtrack(t + 1);//判断
    }
}

 Descripción del problema

Hay n artículos, cada uno de los cuales tiene su propio volumen y valor.Con una mochila de capacidad dada, ¿cómo maximizar el valor total de los artículos cargados en la mochila?
Nota : A diferencia del problema de la mochila común, en el problema de la mochila 0-1, los artículos aparecen como un todo, y solo puede elegir poner el todo en la mochila o no poner el todo en la mochila.

#include <stdio.h>
#include <stdlib.h>
#define N 100
int n, c, maxValue = 0; // 物品数量，背包容量，最大价值
int w[N], v[N]; // 物品重量，物品价值
int path[N];
int path0[N];
void backtrack(int i, int res, int value) {
    if (i == n) {
        if (value > maxValue) {
                maxValue = value;
                for (int i = 0; i < n; i++) path0[i] = path[i];
        }
        return;
    }
    path[i] = 1;
    if (res >= w[i]) {
            backtrack(i + 1, res - w[i], value + v[i]); // 考虑第i个物品放入背包
    }
    path[i] = 0;
    backtrack(i + 1, res, value); // 不考虑第i个物品放入背包
}
 
int main() {
    scanf("%d%d", &n, &c);
    for (int i = 0; i < n; i++) scanf("%d%d", &w[i], &v[i]);
    backtrack(0, c, 0);
    printf("%d\n", maxValue);
    for (int i = 0; i < n; i++) printf("%d ", path0[i]);
    return 0;
}

El problema del viajante de comercio (omitido)

análisis del problema

 código detallado

#include <stdio.h>
#include <stdbool.h>
#define MAXN 100 // 最大城市数
 
int n;             // 城市数
int graph[MAXN][MAXN]; // 图的邻接矩阵
int path[MAXN],bestPath[MAXN];    // 保存当前路径
bool visited[MAXN]; // 标记城市是否访问过
int minDist = 0x7fffffff; // 保存最短路径的长度
 
void backtracking(int cur, int dist) {
    if (cur == n) {  // 所有城市都已经走过了
        if (dist + graph[path[n - 1]][0] < minDist) {
            minDist = dist + graph[path[n - 1]][0]; // 更新最短路径
            for(int i = 0;i < n;i++){
                bestPath[i] = path[i];
            }
        }
        return;
    }
    for (int i = 1; i < n; i++) { // 枚举下一个城市
        if (!visited[i]) {        // 如果这个城市还没有访问过
            path[cur] = i;         // 选择这个城市
            visited[i] = true;     // 标记这个城市已经访问过
            backtracking(cur + 1, dist + graph[path[cur - 1]][i]); // 递归到下一层
            visited[i] = false;    // 回溯，撤销选择
        }
    }
}
 
int main() {
    scanf("%d", &n); // 输入城市数
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &graph[i][j]); // 输入邻接矩阵
        }
    }
    path[0] = 0;       // 起点是城市0
    visited[0] = true; // 标记起点已经访问过
    backtracking(1, 0); // 从第2个城市开始递归
    printf("%d\n", minDist); // 输出最短路径长度
    for(int i = 0;i < n;i++){
        printf("%d ",bestPath[i]+1);
    }
    return 0;
}

 0-1 mochila

 

rama y atado

problema de carga

// 定义MaxLoading子函数，用来求解装载问题
// 输入参数：w是一个整型数组，表示集装箱的重量；c是一个整型变量，表示船舶的载重量；n是一个整型变量，表示集装箱的数量；bestx是一个整型数组，用来存储最优解方案
// 返回值：bestw是一个整型变量，表示最优解值
int MaxLoading(int* w, int c, int n, int* bestx) {
    // 初始化变量
    int i = 1; // 当前扩展节点所在层次
    int j; // 循环计数器
    int bestw = 0; // 最优解值
    Heap h; // 优先队列
    h.length = 0; // 优先队列的长度初始化为0
    int* r = new int[n + 1]; // 剩余集装箱重量之和
    r[n] = 0;
    for (j = n - 1; j > 0; j--)
        r[j] = r[j + 1] + w[j + 1];
    Node* p = new Node; // 当前扩展节点
    p->weight = 0;
    p->level = i;
    p->parent = NULL;
    Node* q; // 新生成节点

    while (i != n + 1) { // 当还未到达叶子节点时循环
        if (p->weight + w[i] <= c) { // 进入左子树，即选择第i个集装箱
            q = new Node; // 创建新节点
            q->LChild = 1; // 标记为左子树
            q->level = p->level + 1; // 层次加一
            q->parent = p; // 父节点指向当前扩展节点
            q->weight = p->weight + w[i]; // 节点重量等于父节点重量加上第i个集装箱重量
            q->uweight = q->weight + r[i]; // 节点上界等于节点重量加上剩余集装箱重量之和
            if (q->level == n + 1 && q->weight > bestw) { // 找到更好解
                bestw = q->weight; // 更新最优解值
                for (j = n; j > 0; j--) { // 更新最优解方案
                    bestx[j] = q->LChild;
                    q = q->parent;
                }
            }
            else { // 将新生成节点插入优先队列
                HeapInsert(h, q);
            }
        }
        if (p->weight + r[i] > bestw) { // 进入右子树，即不选择第i个集装箱，并且满足剪枝条件
            q = new Node; // 创建新节点
            q->LChild = 0; // 标记为右子树
            q->level = p->level + 1; // 层次加一
            q->parent = p; // 父节点指向当前扩展节点
            q->weight = p->weight; // 节点重量等于父节点重量
            q->uweight = q->weight + r[i]; // 节点上界等于节点重量加上剩余集装箱重量之和
            if (q->level == n + 1 && q->weight > bestw) { // 找到更好解
                bestw = q->weight; // 更新最优解值
                for (j = n; j > 0; j--) { // 更新最优解方案
                    bestx[j] = q->LChild;
                    q = q->parent;
                }
            }
            else { // 将新生成节点插入优先队列
                HeapInsert(h, q);
            }
        }
        delete p; // 删除当前扩展节点
        if (!h.empty()) { // 取堆顶元素作为下一个扩展节点，并且堆不为空时继续循环
            HeapDelete(h, p);
            i = p->level;
        }
        else { // 堆为空则结束循环
            break;
        }
        
    }
    delete[] r; // 删除动态数组r
    return bestw; // 返回最优解值
}

problema de camarilla máxima

 

0-1 mochila

aleatorización

Clasificación rápida aleatoria: un algoritmo de clasificación rápida que selecciona aleatoriamente puntos de pivote

código central

void quickSort(int r[], int low, int high)
{
	srand(time(0));
	int i, k;
	if (low<high)
	{
		i=randomNum(low, high); //在区间[low，high]中随机选取一个元素，下标为i
		r[low]←→r[i]; //交换r[low]和r[i]的值
		k=partition(r, low, high); //进行一次划分，得到轴值的位置k
		quickSort(r, low, k-1);//在前半部分继续查找
		quickSort(r, k+1, high);//在后半部分继续查找
	}
}

código completo

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
 
//舍伍德（Sherwood）型随机化算法 随机快速排序：随机选择枢点的快速排序算法
 
//在区间[low，high]中随机选取一个元素，下标为i
int randomNum(int low, int high){
  return low + rand() % (high - low + 1);
}
 
//交换两个元素的值
void swap(int *a, int *b){
  int temp = *a;
  *a = *b;
  *b = temp;
}
 
//进行一次划分，得到轴值的位置k
int partition(int r[], int low, int high){
  int pivot = r[low]; //选取第一个元素作为轴值
  while(low < high){ //循环直到low和high相遇
    while(low < high && r[high] >= pivot) high--; //从右向左找到第一个小于轴值的元素
    swap(&r[low], &r[high]); //交换r[low]和r[high]的值
    while(low < high && r[low] <= pivot) low++; //从左向右找到第一个大于轴值的元素
    swap(&r[low], &r[high]); //交换r[low]和r[high]的值
  }
  return low; //返回轴值的位置
}
 
//快速排序函数
void quickSort(int r[], int low, int high)
{
	srand(time(0));
	int i, k;
	if (low<high)
	{
		i=randomNum(low, high); //在区间[low，high]中随机选取一个元素，下标为i
		swap(&r[low], &r[i]); //交换r[low]和r[i]的值
		k=partition(r, low, high); //进行一次划分，得到轴值的位置k
		quickSort(r, low, k-1);//在前半部分继续查找
		quickSort(r, k+1, high);//在后半部分继续查找
	}
}
 
//打印数组
void printArray(int arr[], int n){
  int i;
  for(i=0; i<n; i++){
    printf("%d ", arr[i]);
  }
  printf("\n");
}
 
//主函数
int main(){
  //定义一个数组，表示10个待排序的数
  int arr[10] = {23, 45, 12, 67, 89, 34, 56, 78, 90, 11};
  //打印原始数组
  printf("原始数组：\n");
  printArray(arr, 10);
  //调用快速排序函数
  quickSort(arr, 0, 9);
  //打印排序后的数组
  printf("排序后的数组：\n");
  printArray(arr, 10);
 
  return 0;
}

Problema de ocho reinas (ppt no tiene código, siento que la probabilidad de la prueba no es alta)

(1) Inicializar la matriz x[8] a 0; inicializar el conteo de tiempos de prueba a 0;

(2) para (i=1; i<=8; i++)     

 2.1 Generar un número aleatorio j de [1, 8];   

 2.2 cuenta=cuenta+1, lleva a cabo la prueba de cuenta;     

 2.3 Si la reina i (fija en la fila i) se coloca en la columna j sin conflicto, entonces x[i]=j; cuenta=0; vaya al paso (2) (el ciclo for continúa ejecutándose) para colocar la siguiente reina;     

  2.4 Si (cuenta == 8), la reina no se puede colocar y el algoritmo falla.       

 Vaya al paso 2.1 para cambiar la posición de la reina i;

(3) Muestra los elementos x[1]~x[8] como solución al problema de las ocho reinas.

#include <iostream>
#include <cstdlib>
#include <ctime>
 
using namespace std;
 
bool isSafe(int x[], int row, int col) {
    // 检查当前位置是否与之前放置的皇后冲突
    for (int i = 1; i < row; i++) {
        if (x[i] == col || abs(i - row) == abs(x[i] - col)) {
            return false;
        }
    }
    return true;
}
 
void solveEightQueens(int x[], int row) {
    if (row > 8) {
        // 所有皇后都放置完成，打印解
        for (int i = 1; i <= 8; i++) {
            cout << x[i] << " ";
        }
        cout << endl;
    } else {
        for (int j = 1; j <= 8; j++) {
            if (isSafe(x, row, j)) {
                x[row] = j;
                solveEightQueens(x, row + 1);
            }
        }
    }
}
 
int main() {
    srand(time(0));
 
    int x[9] = {0}; // 数组从下标 1 开始使用，初始化为0
 
    solveEightQueens(x, 1);
 
    return 0;
}

El significado de la salida del código es el siguiente:

• Cada fila representa una solución, es decir, un esquema de colocación de reina que satisface las condiciones.
• Hay ocho números en cada fila, que indican respectivamente los números de columna de las reinas en las filas primera a octava.
• Por ejemplo, la salida de la primera fila es 4 2 7 3 6 8 5 1, lo que significa que la reina de la primera fila está en la cuarta columna, la reina de la segunda fila está en la segunda columna y así sucesivamente.
• En total, hay 92 soluciones posibles, es decir, 92 esquemas de colocación de reinas diferentes.

problema del elemento principal

código central

bool isMajority(int arr[], int n, int x) {
    int count = 0; // 记录x出现的次数
    for (int i = 0; i < n; i++) {
        if (arr[i] == x) count++;
    }
    return count > n / 2; // 如果x出现次数超过一半，返回true
}

mejoramiento

código completo

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
 
// 在区间[low，high]中随机选取一个整数
int randomNum(int low, int high) {
    return low + rand() % (high - low + 1);
}
 
// 判断一个元素是否是主元素，即出现次数超过一半
bool isMajority(int arr[], int n, int x) {
    int count = 0; // 记录x出现的次数
    for (int i = 0; i < n; i++) {
        if (arr[i] == x) count++;
    }
    return count > n / 2; // 如果x出现次数超过一半，返回true
}
 
// 蒙特卡罗函数，返回数组中的一个主元素，如果不存在，返回-1
int monteCarlo(int arr[], int n) {
    srand(time(0)); // 设置随机数种子
    int k = 10; // 设置最大尝试次数
 
    // 候选主元素初始化为数组的第一个元素
    int candidate = arr[0];
    int count = 1; // 记录候选主元素的计数
 
    for (int i = 1; i < n; i++) {
        if (arr[i] == candidate) {
            count++;
        } else {
            count--;
            if (count == 0) {
                // 当前候选主元素计数为0，更新候选主元素为当前元素
                candidate = arr[i];
                count = 1;
            }
        }
    }
 
    // 最后确定的候选主元素需要再次验证
    if (isMajority(arr, n, candidate)) {
        return candidate; // 如果是，返回该元素
    }
 
    return -1; // 如果不存在主元素，返回-1
}
 
// 打印数组
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
}
 
// 主函数
int main() {
    // 定义一个数组，表示n个待查找的数
    int arr[10] = {3, 3, 4, 4, 2, 4, 2, 4, 4,4};
 
    // 打印原始数组
    cout << "原始数组：\n";
    printArray(arr, 10);
 
    // 调用蒙特卡罗函数，返回数组中的一个主元素
    int result = monteCarlo(arr, 10);
 
    // 打印结果
    if (result == -1) {
        cout << "不存在主元素" << endl;
    } else {
        cout << "一个主元素是：" << result << endl;
    }
 
    return 0;
}