기사 디렉토리
10장 차원축소와 메트릭 학습
10.1kk _k- 최근접 이웃 학습
ㅋㅋK - 최근접 이웃 학습은 일반적으로 사용되는 지도 학습 방법이며 작동 메커니즘은 매우 간단합니다. 테스트 샘플이 주어지면 특정 거리 메트릭을기반으로 훈련 세트에서 가장 가까운 kk를 찾습니다.k 훈련 샘플, 그리고 이kk를k "이웃"의 정보는 예측을 만드는 데 사용됩니다.
일반적으로 "투표 방법"은 분류 작업, 즉 kk를 선택하는 데 사용할 수 있습니다.k 개의 샘플에서 가장 많이 나타나는 범주 표시를 예측 결과로 사용하며, 회귀 작업에서는 "평균 방법", 즉 kk를 사용할 수 있습니다.k 개 샘플의 실제 출력 점수의 평균값을 예측 결과로 사용하며, 거리를 기준으로 가중 평균 또는 가중 투표도 가능하며 샘플이 가까울수록 가중치가 커집니다.
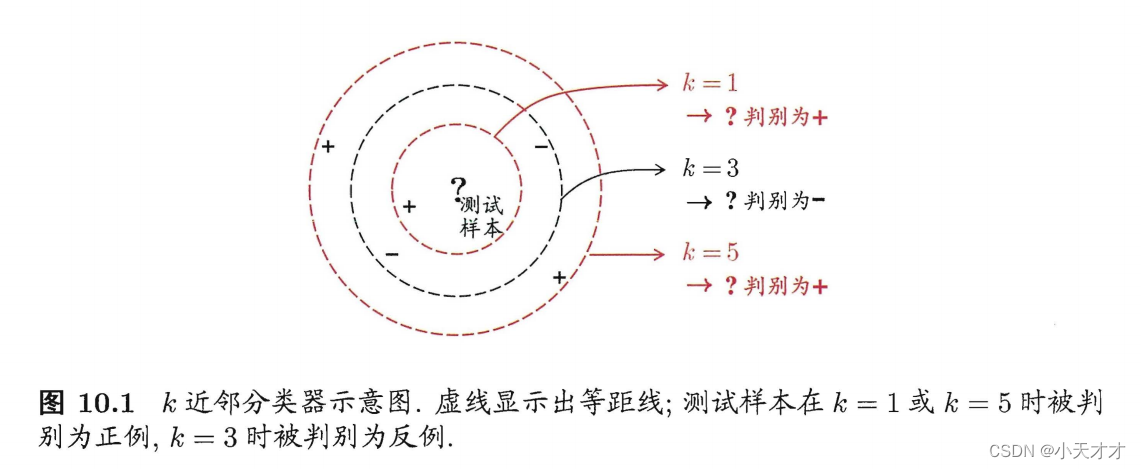
ㅋㅋk- 최근접 이웃 학습에는 세 가지 주요 요인이 포함됩니다.kkk 의 크기 , 거리 또는 유사성의 척도, 특징 정규화. ㅋㅋk 의 크기는 이웃과 투표 가중치의 범위를 결정하고, 거리 또는 유사성의 척도는 두 인스턴스 간의 근접성을 판단하는 방법을 결정하며, 기능 정규화는 거리 또는 유사성 계산에 대한 각 기능의 영향을 결정합니다. 이러한 요소는 모두 특정 문제 및 데이터 세트에 따라 적절한 방법과 매개변수를 선택해야 합니다.
10.2 저차원 임베딩
ㅋㅋk -최근접 이웃 학습은 "조밀한 샘플링" 가정(모든 테스트 샘플xx)x 근처의 모든 작은δ \delta트레이닝 샘플은 항상 δ 거리 범위 내에서 찾을 수 있습니다. 즉, 트레이닝 샘플의 샘플링 밀도가 충분히 큽니다. 그러나 이 가정은 δ = 0.001 \delta=0.001로 가정하면 현실적으로 성립하기 어렵다.디=0.001 , 이는 모든 테스트 샘플이 항상 0.001 근처의 거리 내에서 훈련 샘플을 찾을 수 있도록 정규화된 속성 값 범위 내에서 최소 1000개의 샘플 포인트가 균등하게 분포되어야 함을 의미하며, 이는 차원이 다음과 같은 경우 속성일 뿐입니다. 1, 속성 차원이 크면 필요한 샘플 수가 증가할 뿐만 아니라 고차원 공간으로 인해 거리 계산에 큰 어려움이 있습니다. 따라서 때때로 우리는 차원 감소를 통해 차원의 재난을 완화해야 합니다. 즉, 일부 수학적 변환을 통해 원래의 고차원 속성 공간을 저차원 "하위 공간"으로 변환합니다. 이 하위 공간에서 샘플 밀도가 크게 증가하고 거리 계산도 쉬워집니다.

다음은 다차원 스케일링 방법인 MDS(Multiple Dimensional Scaling)를 소개합니다. 샘플과 주어진 일관성 사이. 차원축소의 관점에서 볼 때 저차원 공간에서의 샘플간 거리/상이성은 기본적으로 고차원 공간에서의 샘플간 거리/상이성이 같아야 한다.
특히 다차원 스케일링 프로세스는 다음 단계로 나눌 수 있습니다.
- 고차원 공간에서 샘플 간의 거리 행렬 DD 계산D , 여기서D ij D_{ij}디이자ii 를 나타냅니다.i번째 샘플과jjthj 샘플 사이의 거리, 일반적으로 유클리드 거리. 이 단계는 차원 축소를 위한 기초로 샘플 간의 유사성 또는 비유사성 정보를 얻는 것입니다.
- 쌍 거리 행렬 DDD는 내적 행렬BB를B , 여기서B ij B_{ij}비이자ii 를 나타냅니다.i번째 샘플과jjthj 개 샘플 사이의 내적센터링 공식은B = − 1 2 HDHB = -\frac {1} {2}HDH비=-21HDH , 여기서 H는 센터링 행렬H = I − 1n 1 1 TH = I - \frac {1} {n}11^T시간=나-N11 1T ,III 는 항등 행렬,1 11 은 모두1 11 벡터. 이 단계는 샘플의 평균값의 영향을 제거하여 샘플이 저차원 공간에서도 평균이 0이 되도록 하여 후속 고유값 분해에 편리합니다.
- 내적 행렬 BB 의 경우B는 고유값 분해를 수행하여 B = V Λ VTB = V\Lambda V^T를얻습니다.비=V Λ VT , 여기서Λ \LambdaΛ 는 대각선에 고유값이 있는 대각선 행렬입니다.VVV 는 고유 벡터의 행렬이고 각 열은 고유 벡터입니다. 이 단계는 저차원 공간에서 샘플의 최적 표현을 찾는 것, 즉 샘플 간의 분산을 최대화하는 것입니다.
- 이전 dd를 가져 가라.d개의 가장 큰 고유값과 해당 고유벡터는Λ d \Lambda_d엘디및 V d V_dV디, 여기서 Λ d \Lambda_d엘디dd 입니다차수 d , V d V_dV디n ∗ dn*dN∗d- 매트릭스. 이 단계는 적절한 차원 감소 대상 차원dd를d 가장 중요한 고유 벡터를 유지하십시오.
- 차원 축소된 데이터 행렬 계산 Z = V d Λ d 1 / 2 Z = V_d \Lambda_d^{1/2}지=V디엘디1/2,그 중 ZZZ 는n ∗ dn*dN∗d 행렬에서 각 행은 저차원 공간에서 샘플의 좌표입니다. 이 단계는 샘플 간의 거리 또는 유사성이 변경되지 않도록 저차원 공간에서 샘플의 특정 좌표를 얻는 것입니다.
차원 축소 효과의 평가 방법은 두 가지 범주로 나눌 수 있습니다.
- 하나는 2차원, 3차원으로 축소한 후 데이터를 시각적으로 분석하는 것으로 상대적으로 주관적인 정성적 평가 기준으로 차원 축소 후의 데이터가 구조와 유사성을 유지하는지 직관적으로 알 수 있다. 원본 데이터..
- 다른 하나는 차원축소 전과 후의 학습자의 성과를 비교하여 평가하는 것으로 보다 객관적인 정량적 평가기준으로 정확도, 재현율, F1값 등 일부 지표로 측정이 가능하다. 이 접근법은 차원 축소가 학습자의 효율성과 효율성을 향상시키는지 여부를 반영할 수 있습니다.
10.3 주성분 분석
10.3.1 정의 및 단계
주성분 분석(PCA)은 가장 널리 사용되는 데이터 차원 감소 알고리즘 중 하나이며, 주요 아이디어 는n 차원 특징은kkk 차원 에서kkk 차원은 원래 nn을기반으로 하는 주성분이라고도 하는 새로운 직교 기능입니다.kk는 n 차원 특징을 기반으로 재구성됨k- 차원 특징.
PCA의 수학적 정의는 다음과 같습니다. 이 데이터의 투영에서 첫 번째로 큰 분산이 첫 번째 좌표(첫 번째 주성분이라고 함)에 있도록 데이터를 새로운 좌표계로 변환하는 직교 선형 변환, 두 번째로 큰 분산은 다음과 같습니다. 두 번째 좌표(두 번째 주성분) 등.
PCA의 역할은 원래 공간에서 상호 직교하는 좌표축 집합을 순차적으로 찾는 것이며, 새로운 좌표축의 선택은 데이터 자체와 밀접한 관련이 있습니다. 그 중 첫 번째 새 좌표축의 선택은 원본 데이터에서 분산이 가장 큰 방향이고, 두 번째 새 좌표축의 선택은 첫 번째 좌표축과 직교하는 평면에서 분산이 가장 큰 방향이며, 세 번째 축은 분산이 가장 큰 방향으로 직교하는 두 평면에서 분산이 가장 큰 방향입니다. 등등, nn을 얻을 수 있습니다.n 그러한 축. 이렇게 얻은 새 축으로 대부분의 분산이 앞kkk 좌표축 중 후자의 좌표축에 포함된 분산은 거의 0입니다. 따라서 나머지 좌표축은 무시하고 앞kk대부분의 분산을 포함하는 k 축. 실제로 이것은 대부분의 분산을 포함하는 차원 기능만 유지하고 데이터 기능에 대한 차원 감소 처리를 달성하기 위해 분산이 거의 0인 기능 차원을 무시하는 것과 같습니다.
가장 큰 변동성을 포함하는 이러한 주성분 방향을 얻으려면 데이터에 대해 몇 가지 전처리 및 계산을 수행해야 합니다. 구체적인 단계는 다음과 같습니다.
- 조직 데이터 세트: mm이 있다고 가정합니다.mnn_ __n 차원 데이터 샘플은 m × nm × n을형성합니다.중×n 행렬XXX。 _
- 평균 계산: 각 기능의 평균을 내고 모든 샘플에서 해당 기능의 평균을 뺍니다.
- 공분산 행렬 계산: 공분산 행렬은 서로 다른 특성 간의 상관 관계를 설명하는 대칭 행렬입니다. 공분산 행렬은 샘플 행렬에 전치를 곱하고 샘플 수에서 1을 뺀 값, 즉 1 m − 1 WWT \frac{1}{ {m - 1}}{\bf{W} }{ {\bf{ W}}^T}m - 11승 승티。
- 공분산 행렬의 고유값과 고유벡터 찾기: 공분산 행렬은 실제 대칭 행렬이며 Q Σ Q − 1 QΣQ^{-1}Q Σ Q− 1 QQ형식Q 는 고유 벡터로 구성된 직교 행렬,Σ ΣΣ 는 고유값의 대각 행렬입니다.
- 주성분 선택: 고유값에 따라 큰 것부터 작은 것까지 정렬, 상위 kk 선택k개의 가장 큰 고유값에 해당하는 고유 벡터는 행렬PP를피。
- 차원 축소 후 데이터 가져오기: 원본 데이터 매트릭스 XXX 배PPP는 차원 축소 후YY를Y。 _
10.3.2 가장 근접한 리팩토링 가능성과 최대 분리 가능성
주성분 분석의 목적은 저차원 초평면을 찾아 이 초평면에 원본 데이터를 투영하면 원본 데이터의 정보를 최대한 유지할 수 있도록 하는 것입니다. 이 정보는 최근 재구성 및 최대 분리 가능성의 두 가지 방법으로 측정할 수 있습니다.
-
가장 가까운 재구성: 재구성된 샘플이 원래 공간에 다시 매핑되고 원래 샘플과의 거리가 충분히 가깝습니다. 즉, PCA는 투영된 데이터가 최소한의 오류로 원본 데이터에 근접할 수 있어야 합니다. 이 오류는 샘플 포인트에서 투영된 초평면까지의 거리로 나타낼 수 있으므로 가장 가까운 재구성성은 거리 제곱의 합을 최소화하는 최적화 문제로 변환될 수 있습니다.
-
최대 분리성: 이 초평면에서 샘플의 투영은 가능한 한 분리됩니다. 즉, PCA는 원래 데이터의 차이를 반영하기 위해 투영된 데이터가 가장 큰 분산을 갖도록 요구합니다. 이 분산은 투영된 데이터의 공분산 행렬로 나타낼 수 있으므로 최대 분리도는 공분산 행렬의 추적을 최대화하는 최적화 문제로 변환될 수 있습니다.
데이터 샘플이 중앙에 있다고 가정합니다. 즉, ∑ xi = 0 \sum { {x_i}} = 0∑엑스나=0 , 투영 변환 후 얻은 새로운 좌표계는{ w 1 , w 2 , . . , wd } \{ {w_1},{w_2},...,{w_d}\}{ 승1,승2,... ,승디} , 새 좌표계의 일부 좌표를 버리면 차원이d ′ < d d' < d디′′<d , 샘플 포인트xi x_i엑스나저차원 좌표계에서의 투영은 zi = ( zi 1 ; zi 2 ; . . ; zid ′ ) {z_i} = ({z_{i1}};{z_{i2}};...;{ z_ {id'}})지나=( 지나는 1;지나는 2;... ;지내가 d′),其中zij = wj T xi {z_{ij}} = w_j^T{x_i}지이자=승제이티엑스나꼭 xi x_i엑스나저차원 좌표계 jjth 에서j -zi z_i를기반으로 하는 경우 차원 좌표지나xi x_i를 재구성하기 위해엑스나, x ‾ i = ∑ j = 1 d ′ zijwj {\overline x _i} = \sum\limits_{j = 1}^{d'} { {z_{ij}}{w_j} }엑스나=j = 1∑디′지이자승j。
전체 훈련 세트, 원래 샘플 포인트 x x_i를 고려하십시오.엑스나그리고 투영 재구성에 기반한 샘플 포인트 x ‾ i {\overline x _i}엑스나之间的距离为
∑ i = 1 m ∥ ∑ j = 1 d ′ zijwj − xi ∥ 2 2 = ∑ i = 1 mzi T zi − 2 ∑ i = 1 mzi TWT xi + const ∝ − tr ( WT ( ∑ i = 1 mxixi T ) W ) \sum\limits_{i = 1}^m {\left\| {\sum\limits_{j = 1}^{d'} {
{z_{ij}}{w_j} - {x_i}} } \right\|_2^2} = \sum\limits_{i = 1}^ m {
{z_i}^T{z_i} - 2\sum\limits_{i = 1}^m {
{z_i}^T{
{\bf{W}}^T}{x_i} + const} } \propto - tr({
{\bf{W}}^T}(\sum\limits_{i = 1}^m { {
x_i}{x_i}^T} ){\bf{W}})나는 = 1∑엠
.j = 1∑디′지이자승j-엑스나
.22=나는 = 1∑엠지나Tz _나-2나는 = 1∑엠지나티 승티 엑스나+비용 _ _ _∝- t r ( 승티 (나는 = 1∑엠엑스나엑스나T )W)
최근접 재구성에 따르면 위 식을 최소화해야 하며 다음과 같은 결과를 얻을 수 있으며 이는 주성분 분석의 최적화 목표이기도 하다.
최소 W − tr ( WTXXTW ) s . t . WTW = I \begin{aligned} \min\limits_{\bf{W}} &- tr({ {\bf{W}}^T}{\bf
{ X}}{
{\bf{X}}^T}{\bf{W}}) \\ st&{ { \
bf{W}}^T}{\bf{W}} = {\bf{I} } \\ \end{정렬}여분에스 . 티 .-t r ( 승T XX티 승)여티 승=나
최대 분리도에 따라 모든 표본점의 투영을 최대한 분리하면 아래 그림과 같이 투영된 표본점의 분산이 최대화되어야 합니다. 따라서 공분산 행렬 XXT {\bf{X}}{
{\bf{X}}^T}X XT는 고유값 분해를 수행하고 얻은 고유값을 정렬합니다:λ 1 ⩾ λ 2 ⩾ .엘1⩾엘2⩾...⩾엘디, 그런 다음 이전 d 'd'를 취하십시오.디고유값에 해당하는 고유벡터는 W ∗ = ( w 1 , w 2 , . . , wd ′ ) {
{\bf{W}}^*} = ({w_1},{w_2},... ,{w_{d'}})여∗=( 승1,승2,... ,승디′) 주성분 분석 솔루션입니다.

10.4 커널화된 선형 차원 감소
실제 작업에서는 적절한 저차원 임베딩을 찾기 위해 비선형 매핑이 필요할 수 있습니다.아래 그림과 같이 샘플 포인트는 2차원 공간의 직사각형 영역에서 샘플링된 다음 S자형 표면 선형차원축소법을 그대로 사용하면 3차원 공간에서 관찰되는 샘플점의 차원이 축소되면 원래의 저차원 구조가 손실된다. "원래 샘플링된" 저차원 공간과 차원 감소 후의 저차원 공간을 구별하기 위해, 우리는 이전의 "진정한" 저차원 공간을 호출합니다. 선형 차원 감소 방법에 대한 커널 기술은 "커널화"를 수행합니다.

10.5 다양한 학습
매니폴드 학습은 고차원 공간의 데이터가 실제로 저차원 매니폴드에 의해 고차원 공간에 매핑된다는 가정을 기반으로 하는 비선형 차원 감소 기법입니다. 매니폴드는 고차원 공간에서 저차원 공간의 곡선이나 표면을 고차원 공간에서 일반화한 것으로 볼 수 있는 고차원 공간의 기하학적 구조입니다. 매니폴드 학습의 목적은 고차원 공간의 데이터를 저차원 매니폴드에 투영하여 데이터 고유의 구조와 특성을 보존할 수 있는 적절한 매핑 함수를 찾는 것입니다. 매니폴드 학습에는 데이터 시각화, 데이터 압축, 데이터 생성, 기능 추출 등과 같은 많은 응용 프로그램이 있습니다. 다양한 학습을 위한 일반적인 알고리즘에는 LLE(Local Linear Embedding), LE(Laplacian Eigenmap), LPP(Local Preserving Projection), ISOMAP(Isometric Mapping) 등이 있습니다.
10.6 메트릭 학습
메트릭 학습은 데이터로부터 데이터 객체 간의 거리 척도를 학습하는 방법으로 학습된 거리 메트릭 하에서 유사한 객체 간의 거리를 작게 만들고 유사하지 않은 객체 간의 거리를 크게 만드는 것이 목적입니다. 메트릭 학습은 데이터 분류, 클러스터링, 검색, 시각화 및 기타 작업에 사용할 수 있습니다.
딥 메트릭 러닝은 딥 러닝과 메트릭 러닝을 결합한 방법으로 원시 데이터에서 고품질의 특징 표현을 자동으로 학습하고 활성화 함수를 활용하여 데이터의 비선형 특성을 포착할 수 있습니다. 심층 메트릭 학습은 주로 샘플 마이닝, 모델 구조 및 손실 함수의 세 가지 측면으로 구성됩니다. 샘플 마이닝은 모델이 어려운 샘플에서 더 많은 정보를 학습할 수 있도록 모델을 교육하기 위해 데이터 세트에서 적절한 샘플 쌍 또는 트리플을 선택하는 것을 말합니다. 모델 구조는 심층 신경망을 사용하여 데이터의 특징 벡터를 추출하는 것을 말하며 일반적인 모델 구조에는 Siamese 네트워크와 triplet 네트워크²가 포함됩니다. 손실함수는 모델 최적화를 정의하는 목적함수를 말하며 대표적인 손실함수로는 Contrastive Loss, Triplet Loss, N-pair Loss가 있다.