Pregunta: En el sistema de coordenadas del plano bidimensional, para cualquier polígono, se conocen las coordenadas de cada vértice y se calcula el área del polígono.
Cuando vi las palabras "coordenadas" y "área", lo primero que pensé fue el contenido del último blog que acabo de escribir: el producto externo de vectores. Luego tratamos de comenzar desde el producto exterior del vector para ver si podemos responder el problema de calcular el área.
Definición de producto exterior vectorial:
Si dos vectores
Entonces =
Para facilitar el cálculo y la derivación, desarrollamos aún más la fórmula de definición del producto exterior, de la siguiente manera:
=
=
=
Reducción de dimensionalidad a un plano bidimensional, ponemos , obtenemos
=
=
, que
representan los vectores unitarios del eje x, eje y y eje z respectivamente.
Debido a que en la tercera columna, excepto la primera fila, todas las demás filas son 0, por lo que desarrollamos de acuerdo con la tercera columna del determinante y obtenemos
=
=
=
, que
representa
el cofactor algebraico.
Entonces, cuando calculamos el producto exterior de dos vectores en un plano bidimensional, podemos evaluarlo calculando el determinante de la matriz ordenada de coordenadas de los dos vectores. En el blog anterior hemos comprobado que el valor absoluto del producto exterior de dos vectores es igual al doble del área del triángulo encerrado por el origen y los tres puntos.
Con esta base en su lugar, volvamos a la pregunta.
El problema describe un polígono, comencemos con el polígono más simple: un triángulo, como se muestra en la siguiente figura:
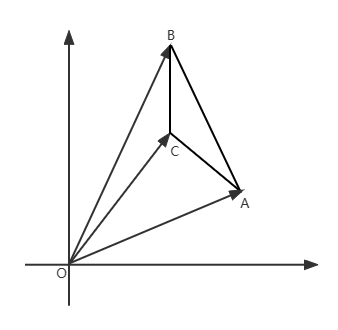
El área del triángulo de la figura anterior es igual a
Usamos el producto externo del vector para traer el área de cada triángulo en la fórmula anterior, podemos obtener
=
Nota: Cuando los vectores se multiplican en cruz, el resultado será positivo o negativo, y el positivo y el negativo representan la dirección que satisface la regla de la mano derecha.
Después de calcular los triángulos, pasamos a los cuadriláteros.
El cuadrilátero se vuelve un poco más complicado, porque el cuadrilátero tiene los llamados lados convexos y cóncavos. Intentemos ver si los dos escenarios pueden tener la misma idea de cálculo, es decir, sin sentido de baches. Primero calculamos los dos gráficos por separado.
Forma convexa:
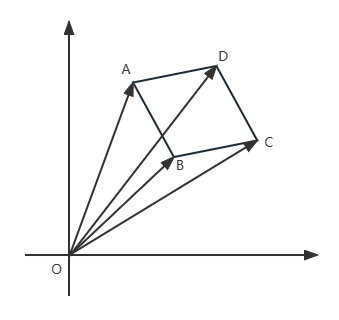
=
=
Forma cóncava:
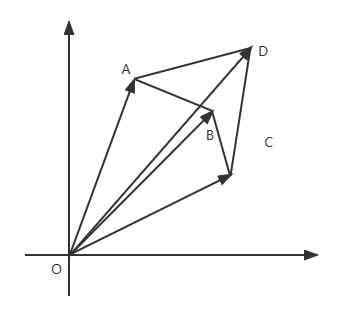
=
=
Se encuentra que las fórmulas de los resultados superior e inferior están unificadas, es decir, los lados convexos y cóncavos del cuadrilátero. Cuando se usa el producto exterior vectorial para el cálculo del área, la fórmula de cálculo es consistente y no hay sensación de golpes. .
Ahora hemos verificado un método de resolución de problemas de triángulos a cuadriláteros, que es:
Los vectores compuestos por cada vértice y el origen del polígono, en sentido contrario a las agujas del reloj (o en el sentido de las agujas del reloj, también se puede utilizar), y los dos vectores anteriores y posteriores se multiplican en cruz para encontrar el producto exterior, y los vectores de la cola y la cabeza también se multiplican en cruz (en otras palabras, es decir, los dos extremos conectados por cada borde del gráfico deben multiplicarse en cruz por la cabeza a la cola ), y luego el valor absoluto de la mitad de la suma obtenida al sumar todos los productos exteriores es el área del polígono. Ahora mismo
=
¿Se puede aplicar este método de cálculo a todos los polígonos? Probémoslo por inducción matemática.
Suponiendo que cuando hay n lados, =
es verdadero, entonces agregue un punto sobre esta base en este momento
para convertirse en n+1 lados
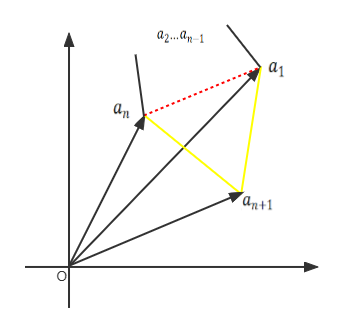
Como se muestra en la figura anterior, necesitamos agregar dos bordes (la parte amarilla en la figura) y eliminar
este borde (la línea de puntos roja en la figura), luego
= +
= +
(Nota: Esto corresponde a agregar dos lados y quitar un lado)
=
El resultado final satisface las reglas de cálculo que resumimos anteriormente. Hasta ahora hemos obtenido teóricamente la solución del área del polígono.
Luego, a continuación, debemos trasplantar este método de cálculo a la computadora y dejar que la computadora realice el cálculo por nosotros, por lo que debemos continuar desarrollando la fórmula de cálculo en una forma que sea conveniente para que la computadora calcule.
=
=
=
=
Entre ellos, en ese momento ,
es decir
Finalmente, obtuvimos la fórmula anterior, que es el famoso teorema del cordón .
¿Cuáles son sus características? Tomemos prestadas imágenes de Internet, de la siguiente manera:
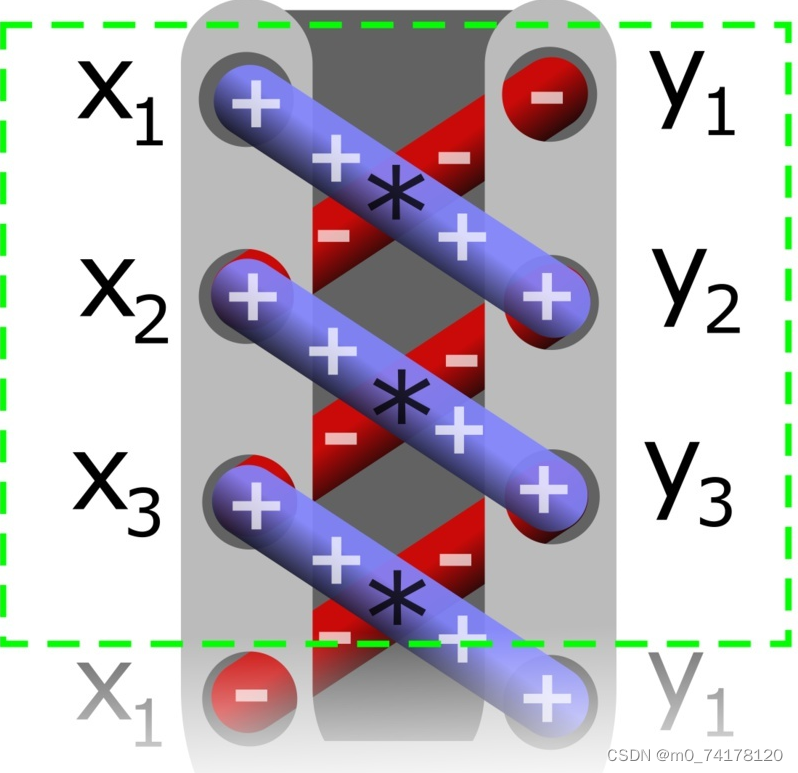
Debido a que esta fórmula funciona como un cordón de zapatos, se llama el teorema del cordón de zapatos.
Con el teorema del cordón de zapato, podemos convertirlo fácilmente en código.
struct Point2d
{
double x;
double y;
Point2d(double xx, double yy): x(xx), y(yy){}
};
//计算任意多边形的面积,顶点按照顺时针或者逆时针方向排列
double ComputePolygonArea(const vector<Point2d> &points)
{
int point_num = points.size();
if(point_num < 3)return 0.0;
double s = 0;
for(int i = 0; i < point_num; ++i)
s += points[i].x * points[(i+1)%point_num].y - points[i].y * points[(i+1)%point_num].x;
return fabs(s/2.0);
}