En la estrategia de divide y vencerás, resolvemos un problema de forma recursiva y se aplican los siguientes tres pasos en cada nivel de recursividad:
1. Descomposición. Divida el problema en algunos subproblemas, la forma de los subproblemas es la misma que la del problema original, pero en menor escala.
2. Resolver. Resuelva los subproblemas de forma recursiva. Si el tamaño de los subproblemas es lo suficientemente pequeño, detenga la recursividad y resuelva directamente.
3. Fusionar. Combine las soluciones de los subproblemas en la solución del problema original.
Cuando el subproblema es lo suficientemente grande como para resolverlo de forma recursiva, lo llamamos caso recursivo. Cuando el subproblema se vuelve lo suficientemente pequeño como para que la recursividad ya no sea necesaria, decimos que la recursividad ha tocado fondo y ha entrado en la situación básica.
Las expresiones recursivas pueden tener muchas formas. Un algoritmo recursivo puede dividir el problema en subproblemas de diferentes tamaños, como la división de 1/3 y 2/3. Y el tamaño del subproblema no tiene por qué ser una proporción fija del problema original.
En aplicaciones prácticas, ignoraremos algunos detalles técnicos de declaración y solución recursivas, como llamar a MERGE-SORT en n elementos. Cuando n es un número impar, las escalas de los dos subproblemas son n / 2 redondeadas hacia arriba y hacia abajo, respectivamente Entero, no exactamente n / 2. Las condiciones de contorno son otro tipo de detalles que generalmente se pasan por alto. Cuando n es lo suficientemente pequeño, el tiempo de ejecución del algoritmo es θ (1), pero no cambiamos la fórmula recursiva de que n es lo suficientemente pequeño para encontrar T (n), porque estos los cambios no excederán un factor constante, por lo que el orden de crecimiento de la función no cambiará.
Invertir en acciones solo se puede comprar y vender una vez, para maximizar la rentabilidad, es decir, comprar al precio más bajo y vender al precio más alto, pero el precio más bajo puede aparecer después del precio más alto
:! [Insertar descripción de la imagen aquí] (https: // img- blog.csdnimg.cn/20210320124004302.png?x-oss- process = image / watermark, type_ZmFuZ3poZW5naGVpdGk, shadow_10, text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3R1,
piensa en el precio más alto cuando puedas vender o vender al precio más alto que puedas precio más alto, o al precio más bajo que crea que puede maximizar los ingresos. Si esta estrategia es efectiva, es muy simple determinar los ingresos máximos: busque el precio más alto y el precio más bajo, y luego comience desde el precio más alto hasta la izquierda para encontrar el precio más bajo a la izquierda, y comience desde el precio más bajo hacia la derecha para encontrar el precio más alto de la derecha, y luego tome los dos pares de precios con la mayor diferencia, pero la siguiente figura es una contraposición ejemplo: el
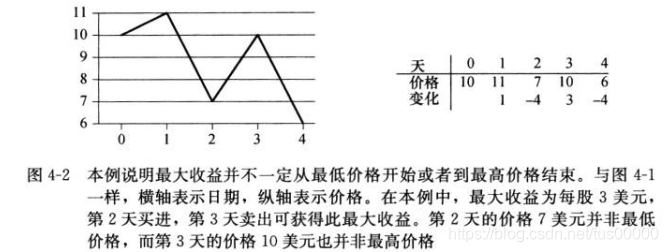
problema anterior se puede resolver simplemente con violencia, pruebe todas las combinaciones posibles de fechas de compra y venta, siempre que la fecha de venta sea la fecha de compra posterior a la lata, un total de n(n-1)/2tipos de combinación de fechas de n días y el El tiempo de procesamiento empleado para cada fecha es al menos constante, por lo tanto, este método de tiempo de funcionamiento Ω (n²).
Podemos examinar los cambios de precio diarios. El cambio de precio en el i-ésimo día se define como la diferencia de precio entre el i-ésimo día y el i-1 ° día. Entonces el problema es encontrar la submatriz continua no vacía más grande , llamado esta submatriz La matriz es la submatriz más grande: El
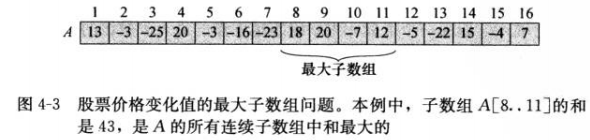
problema de la submatriz más grande es significativo solo cuando la matriz contiene números negativos. Si todos los elementos de la matriz son no negativos, la submatriz más grande es la suma de la totalidad formación.
Considere usar la tecnología de dividir y conquistar para resolver el mayor problema de submatriz. Usar la tecnología de dividir y conquistar significa que tenemos que dividir la submatriz en dos submatrices del mismo tamaño posible, es decir, encontrar la posición central en el medio del subarreglo, y luego considere resolver los dos subarreglos A [bajo ... medio] y A [medio + 1 ... alto], la posición de cualquier subarreglo continuo A [i ... j] de Un [bajo ... alto] debe ser una de las siguientes tres situaciones:
1. Completamente ubicado en el subarreglo En A [bajo ... medio], en este momento bajo <= i <= j <= medio.
2. Está completamente ubicado en el sub-arreglo A [medio + 1… alto], en este momento mid <i <= j <= alto.
3. Cruce el punto medio, en este momento bajo <= i <= medio <= j <= alto.
De hecho, un subarreglo más grande de A [bajo ... alto] debe estar completamente ubicado en A [bajo ... medio], completamente ubicado en A [medio + 1 ... alto] y el más grande de todos los subarreglos en el punto medio. , es posible resolver recursivamente las submatrices más grandes que están completamente ubicadas en ambos lados, por lo que todo el trabajo restante es encontrar la submatriz más grande que abarca el punto medio y luego elegir la suma más grande en estos tres casos:
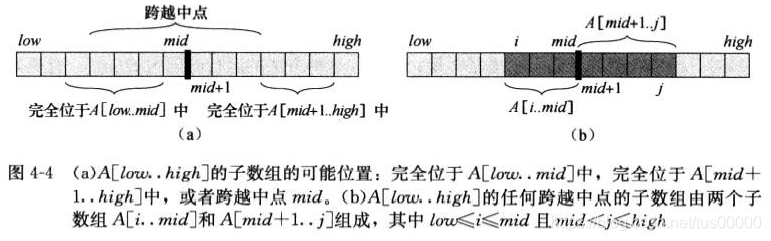
encuentre la submatriz más grande que abarque el punto medio:
FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
left-sum = -∞
sum = 0
for i = mid down to low
sum = sum + A[i]
if sum > left-sum
left-sum = sum
max-left = i
right-sum = -∞
sum = 0
for j = mid + 1 to high
sum = sum + A[j]
if sum > right-sum
right-sum = sum
max-right = j
return (max-left, max-right, left-sum + right-sum)
El proceso anterior toma θ (n) tiempo.
Con el pseudocódigo de tiempo lineal anterior, puede escribir el siguiente pseudocódigo del algoritmo de dividir y conquistar para resolver el problema de subarreglo más grande:
FIND-MAXIMUM-SUBARRAY(A, low, high)
if high == low // base case: only one element
return (low, high, A[low])
else
mid = floor((low + high) / 2) // 向下取整
(left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A, low, mid)
(right-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid + 1, high)
(cross-low, cross-high, cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
if left-sum >= right-sum and left-sum >= cross-sum
return (left-low, left-high, left-sum)
elseif right-sum >= left-sum and right-sum >= cross-sum
return (right-low, right-high, right-sum)
else
return (cross-low, cross-high, cross-sum)
La complejidad temporal de esta solución es θ (nlgn).
Implementación en C ++ del proceso anterior:
#include <iostream>
#include <vector>
using namespace std;
int findMaxCrossSubarray(const vector<int> &nums, size_t start, size_t mid, size_t end) {
int leftSum = 0;
int sum = 0;
for (size_t i = mid + 1; i > start; --i) {
sum += nums[i - 1];
if (sum > leftSum) {
leftSum = sum;
}
}
int rightSum = 0;
sum = 0;
for (size_t i = mid + 1; i <= end; ++i) {
sum += nums[i];
if (sum > rightSum) {
rightSum = sum;
}
}
return leftSum + rightSum;
}
int findMaximumSubarray(const vector<int>& nums, size_t start, size_t end) {
if (start == end) {
return nums[start];
}
size_t mid = (start + end) >> 1;
int leftMax = findMaximumSubarray(nums, start, mid);
int rightMax = findMaximumSubarray(nums, mid + 1, end);
int crossMax = findMaxCrossSubarray(nums, start, mid, end);
return max(leftMax, max(rightMax, crossMax));
}
int main() {
vector<int> ivec = {
13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7 };
cout << findMaximumSubarray(ivec, 0, ivec.size() - 1);
}
Encuentre la submatriz más grande de forma no recursiva y lineal, y la complejidad de tiempo es O (n):
#include <iostream>
#include <vector>
#include <limits>
using namespace std;
int findMaximumSubarray(const vector<int>& nums, size_t start, size_t end) {
int sumMax = numeric_limits<int>::min();
int curSum = 0;
for (size_t i = 0; i < nums.size(); ++i) {
curSum += nums[i];
if (curSum > sumMax) {
sumMax = curSum;
}
if (curSum < 0) {
curSum = 0;
}
}
return sumMax;
}
int main() {
vector<int> ivec = {
13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7 };
cout << findMaximumSubarray(ivec, 0, ivec.size() - 1);
}
Pseudocódigo de multiplicación de matrices:
SQUARE-MATRIX-MULTIPLY(A, B)
n = A.rows
let C be a new nXn matrix
for i = 1 to n
for j = 1 to n
cij = 0
for k = 1 to n
cij = cij + aik * bkj
return C
La multiplicación de matrices no requiere necesariamente Ω (n³) tiempo. Incluso la definición natural de multiplicación de matrices requiere tantas multiplicaciones escalares. Existe el algoritmo recursivo de multiplicación de matrices de Strassen, que tiene una complejidad de tiempo de O (n 2.81 ).
Por simplicidad, se supone que la matriz es nXn, donde n es una potencia de 2, y luego dividir la matriz nXn en 4 sub-matrices de n / 2XN / 2 Las propiedades de una operación de matriz son las siguientes:. La
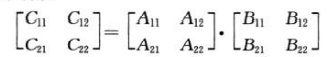
siguiente fórmula es equivalente a la fórmula anterior: de
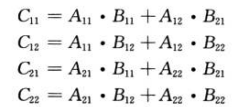
acuerdo con lo anterior El proceso puede escribir pseudocódigo:
SQUARE-MATRIX-MULTIPLY-RECURSIVE(A, B)
n = A.rows
let C be a new nXn matrix
if n == 1
c11 = a11 * b11
else
C11 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11, B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12, B21)
C12 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11, B12) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12, B22)
C21 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21, B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22, B21)
C22 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21, B12) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22, B22)
return C
El código anterior oculta un detalle sutil pero importante de cómo descomponer la matriz. Si realmente creamos 12 nuevas matrices n / 2Xn / 2, tomará θ (n²) tiempo para copiar los elementos de la matriz. De hecho, podemos pasar el subíndice Para especificar una submatriz.
En el proceso anterior, la quinta línea toma θ (1) tiempo para calcular la matriz de descomposición, y luego SQUARE-MATRIX-MULTIPLY-RECURSIVE se llama ocho veces. Cada llamada completa la multiplicación de dos matrices n / 2Xn / 2, por lo que el el tiempo total empleado es 8T (N / 2). En este proceso, se necesita tiempo θ (n²) para llamar a la suma de la matriz 4 veces, por lo que el tiempo total del caso recursivo es:
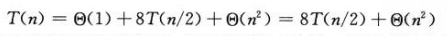
si la descomposición de la matriz se realiza copiando los elementos , el costo requerido es θ (n²), el tiempo total de funcionamiento se incrementará en un factor constante y T (n) permanecerá sin cambios. Por lo tanto, la fórmula del tiempo de ejecución es la siguiente:
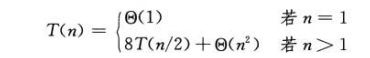
Este método T (n) = θ (n³), por lo que el algoritmo simple de divide y vencerás no es mejor que el método directo.
En la fórmula de T (n), θ (n²) en realidad omite los coeficientes constantes antes de n², porque el símbolo θ ya contiene todos los coeficientes constantes, pero el 8 en la fórmula 8T (n / 2) no se puede omitir, porque 8 representa un árbol recursivo Cada nodo tiene varios nodos secundarios, lo que determina cuántos elementos cada capa del árbol contribuye a la suma.Si se omite 8, el árbol recursivo se convierte en una estructura lineal.
La idea central del algoritmo de Strassen es hacer que el árbol recursivo sea un poco menos exuberante, es decir, que solo realice de forma recursiva siete veces en lugar de ocho multiplicaciones de matrices n / 2Xn / 2. El costo de reducir una multiplicación de matrices puede ser un costo adicional número de adición de matrices n / 2Xn / 2, pero solo tiempos constantes. El algoritmo incluye los siguientes pasos. Los pasos 2 a 4 explicarán los pasos específicos más adelante:
1. Descomponga la matriz de acuerdo con el índice. El método es el mismo que el método recursivo ordinario, y lleva θ (1) tiempo.
2. Cree 10 matrices n / 2Xn / 2, cada matriz guarda la suma o diferencia de las dos submatrices creadas en el paso 1, y lleva tiempo θ (n²).
3. Usando la submatriz creada en el paso 1 y las 10 matrices creadas en el paso 2, calcule de forma recursiva 7 productos de la matriz, y el resultado de cada producto de la matriz es n / 2Xn / 2.
4. Calcule C11, C12, C21 y C22 de la matriz de resultados C con base en el resultado del producto de la matriz en el paso 3.
Los pasos 1, 2 y 4 emplean un total de θ (n²) tiempo, y el paso 3 requiere 7 veces n / 2Xn / 2 multiplicaciones de matrices, por lo que se obtiene el tiempo de ejecución T (n) del algoritmo de Strassen:
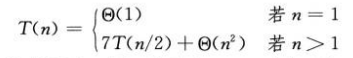
T (n) = θ (n) lg7 ), lg7 está entre 2,80 y 2,81.
En el paso 2 del algoritmo de Strassen, se crean las siguientes 10 matrices: Los
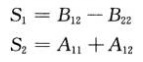
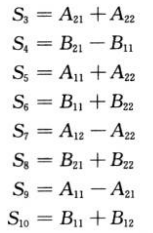
pasos anteriores calculan 10 sumas y restas de n / 2Xn / 2 matrices, lo que lleva θ (n²) tiempo.
En el paso 3, calcule recursivamente la multiplicación de la matriz n / 2Xn / 2 7 veces: en la
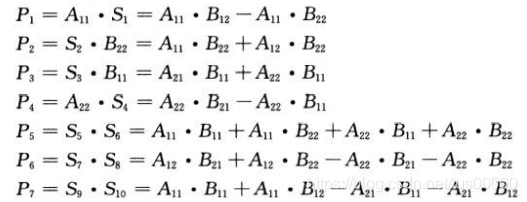
fórmula anterior, solo se debe calcular realmente la multiplicación en la columna del medio, y la columna de la derecha solo ilustra la relación entre estos productos y el submatriz creada en el paso 2.
Paso 4 Realice operaciones de suma y resta en la matriz creada en el Paso 3:
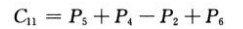
Expanda el lado derecho de la fórmula anterior:
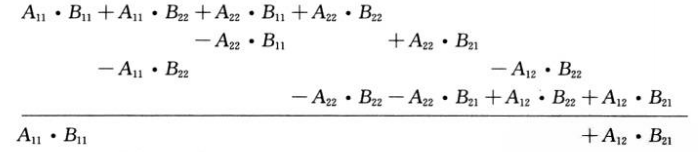
y C12 es igual a:
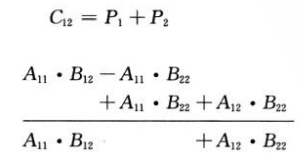
C21 es igual a:
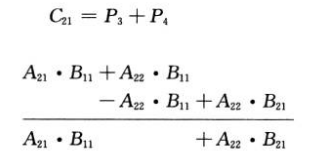
C22 es igual a:
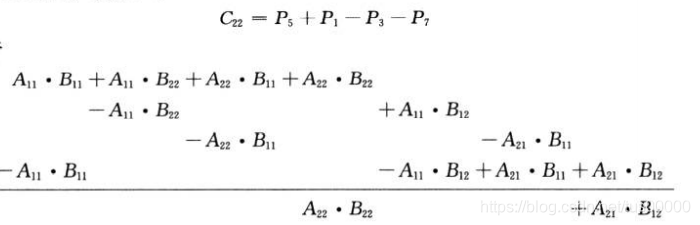
Método de sustitución para resolver la fórmula recursiva:
1. Adivina la forma de la solución.
2. Utilice la inducción matemática para encontrar las constantes en la solución y demuestre que la solución es correcta.
El método de sustitución se puede utilizar para encontrar el límite superior de la siguiente fórmula recursiva:
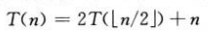
suponemos que la solución es O (nlgn), y el método de sustitución requiere una prueba de que si la constante c> 0 se selecciona adecuadamente, puede haber T (n ) <= cnlgn. El entero m <n es verdadero, especialmente para m = ⌊n / 2⌋, hay T (⌊n / 2⌋) <= c⌊n / 2⌋lg (⌊n / 2⌋) , que se sustituye en la fórmula recursiva, Get:
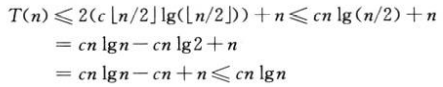
Entre ellos, siempre que c> = 1, se establecerá el último paso. El método de inducción matemática requiere una prueba de que la solución también es válida bajo las condiciones de contorno. Suponga que T (1) = 1 es la única condición de contorno (condición inicial) de la fórmula recursiva. Para n = 1, la condición de contorno T (n ) <= cnlgn deriva T (1) <= c1lg1 = 0, lo que contradice T (1) = 1. En este momento, n se puede extender, tomando n = 2 como la condición de frontera, y T (2) = 4 y T (3) = se puede calcular a partir de la fórmula recursiva 5. En este momento, se puede completar la prueba inductiva: para una cierta constante c> = 1, T (n) <= cnlgn, el método es elegir un valor suficientemente grande c para satisfacer T (2) <= c2lg2 y T (3) <= c3lg3.
Pero el método de sustitución no tiene un método universal para adivinar la solución recursiva correcta. Adivinar la solución requiere experiencia y ocasionalmente creatividad. Puede tomar prestado un árbol recursivo para hacer una buena suposición. Si la fórmula recursiva es similar a la fórmula recursiva que ha visto, es razonable adivinar una solución similar, como la siguiente fórmula recursiva:
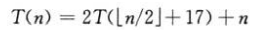
En comparación con el ejemplo anterior, es solo +17. Cuando n es grande, está cerca an Mitad, así que adivina T (n) = O (nlgn), esta suposición es correcta.
Otro buen método de adivinación es probar primero los límites superior e inferior sueltos de la fórmula recursiva y luego reducir el rango de incertidumbre. Como en el ejemplo anterior, puede comenzar desde el límite inferior Ω (n), porque la fórmula recursiva contiene el término n. Podemos probar un límite superior O (n²), y luego gradualmente bajar el límite superior y subir el límite inferior hasta que converja al límite asintóticamente compacto θ (nlgn).
A veces, se adivina el límite asintótico, pero la prueba inductiva falla. En este momento, modifique la conjetura y reste un término de orden inferior. La prueba matemática a menudo puede proceder sin problemas, como la siguiente fórmula recursiva:
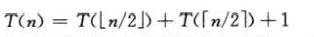
suponemos que la solución es T (n) = O (N), y trate de demostrar que para una constante c adecuada, T (n) <= cn es verdadera, sustituya la conjetura en la fórmula recursiva y obtenga:
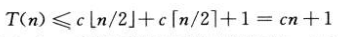
Pero esto no significa que para cualquier c, T (n) <cn, Podemos adivinar un límite mayor, como T (n) = O (n²), aunque el resultado puede inferirse, el original T (n) = O (n) es correcto.
Hacemos una nueva suposición: T (n) <= cn-d, d es una constante ≥0, y ahora hay:
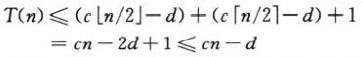
mientras d≥1, esta fórmula se cumple, entonces, como antes, elija una c lo suficientemente grande para tratar con la condición de contorno.
Puede encontrar que la idea de restar un término de orden inferior es contraria a la intuición. Después de todo, si el límite superior resulta infructuoso, la conjetura debe aumentarse en lugar de disminuir, pero un límite más flexible no es necesariamente más fácil de probar. porque para probar un límite superior más débil, se debe usar el mismo límite más débil en la prueba inductiva.
En el ejemplo anterior, podemos tener la siguiente prueba incorrecta:
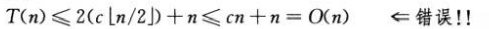
debido a que c es una constante, el error es que no hemos probado una forma que sea estrictamente consistente con la hipótesis de inducción, es decir, T (n) ≤cn.
El resto es demasiado difícil de aprender, tal vez más tarde.