concepto basico
Imagen:
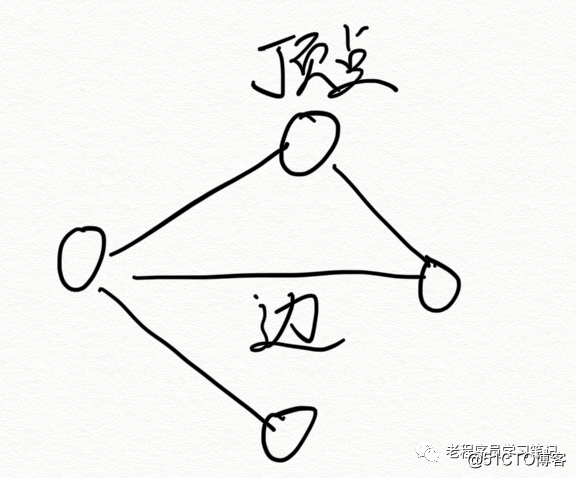
Consta de vértices y aristas. Dividido en
Gráfico dirigido:
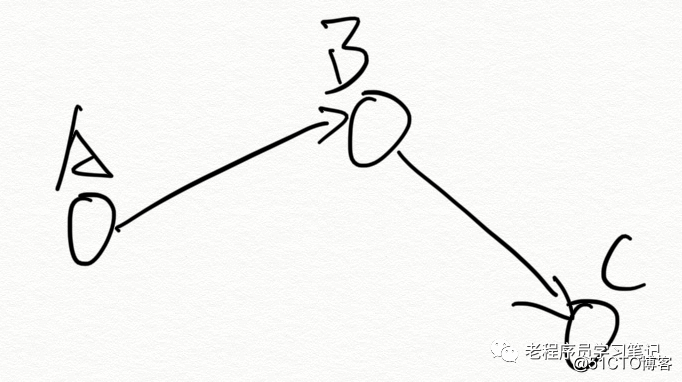
Aquí solo se puede ir de A a B, no de B a A.
Gráfico no dirigido:

Puede ser de A a B, o de B a A, que también se puede representar mediante la siguiente figura:

La otra es agregar peso al borde para convertirse en un gráfico ponderado:
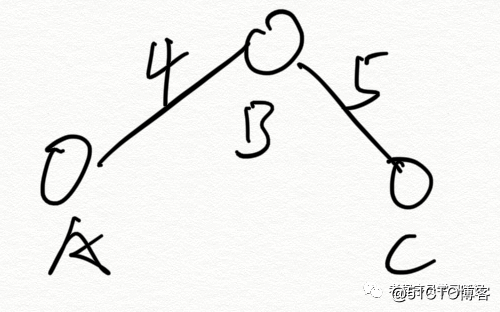
El peso representa el grado de conexión entre los dos vértices, que puede ser tiempo, distancia, peaje, etc., dependiendo de la situación real.
Ruta más corta:
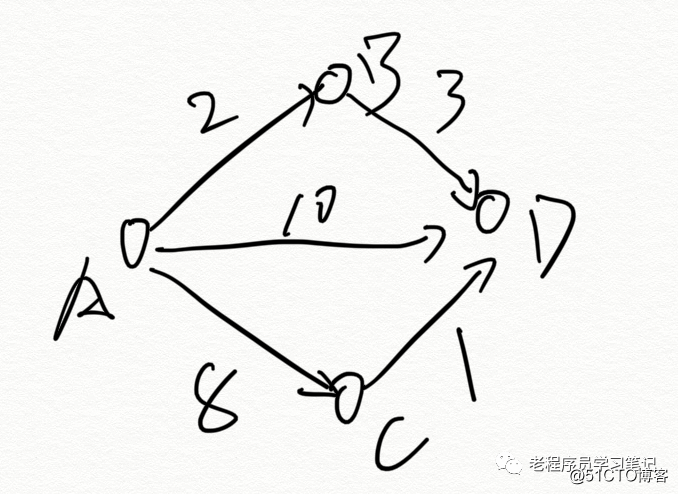
Como se muestra arriba, hay tres rutas de A a D: ABD, AD y ACD.
Considerando el peso de los bordes (como los peajes), el camino más corto entre las tres líneas no es AD (10) con dos puntos conectados directamente, sino ABD (2 + 3 = 5).
Bucle negativo:
Aunque desde la escena real, es difícil imaginar que el peso del borde sea negativo, nunca he oído hablar de ir de A a B a alta velocidad, sin pagar una tarifa de alta velocidad, pero también buscando dinero.
Pero teóricamente, aún debemos considerar la existencia de bordes de peso negativos, lo que conduce a un problema: la existencia de bucles negativos hace que sea imposible encontrar el camino más corto.
Mira la foto de abajo:
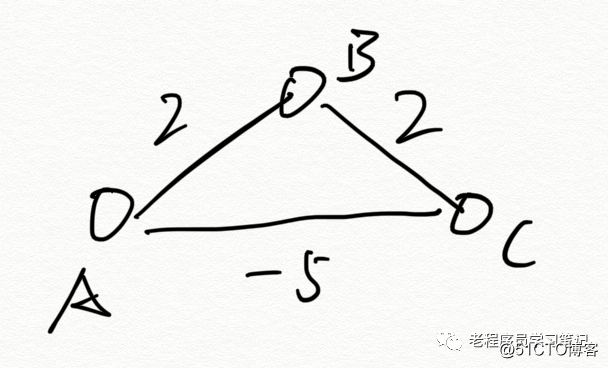
De A a A, el costo es 0, que es el camino más corto, pero debido a la existencia de aristas de peso negativas, causará:
ABCA, el peso es 2 + 2-5 = -1, es decir, A hace un círculo y se convierte en -1, que es menor que 0, y el camino más corto es ABCA.
Esto aún no ha terminado, haga otro círculo, -1 + 2 + 2-5 = -2, A se convierte en -2, y el ciclo continúa, el peso de A a A será cada vez más pequeño.
Este es un bucle negativo y nunca se encontrará el camino más corto.
Por supuesto, tener bordes de peso negativos no significa que deba haber un bucle negativo, como se muestra en la siguiente figura:
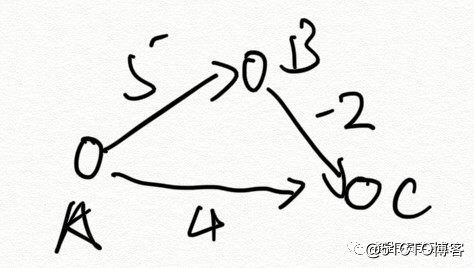
Esto no forma un bucle negativo, el camino más corto de A a C es ABC = 3
Búsqueda de amplitud primero:
En pocas palabras, comienza desde el nodo raíz, después de buscar sus nodos secundarios, y luego busca los nodos secundarios de los nodos secundarios hasta que se encuentra el nodo de destino o se recorren todos los nodos.
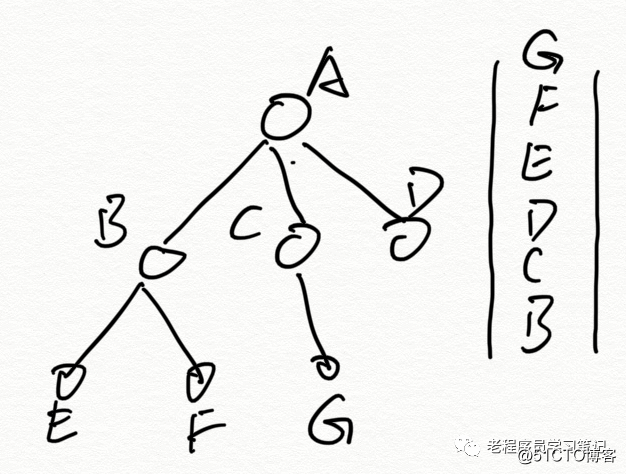
Como se muestra en la figura anterior, coloque el nodo secundario BCD del nodo raíz A en la cola, saque B, luego coloque el nodo secundario EF de B en la cola, luego saque C y luego coloque el nodo secundario G de C en la cola, según las características de la cola de primero en entrar, primero en salir, atraviesa todos los nodos.
Búsqueda profunda primero:
Comenzando desde el nodo raíz, después de buscar una rama, busque otra rama.
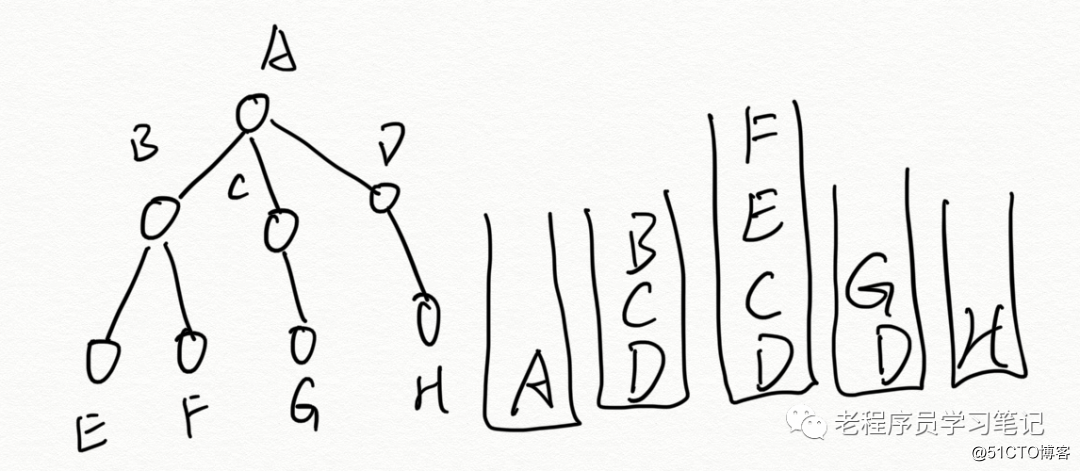
Como se muestra arriba, tome el nodo raíz A y empújelo en la pila.
Saque A, obtenga el nodo hijo BCD de A y empújelo hacia la pila.
Saque B, obtenga el nodo hijo EF de B y empújelo hacia la pila.
Saque F, no hay un nodo hijo y no es el nodo de destino, tire. E es lo mismo.
Saque C, obtenga el nodo hijo G de C y empújelo hacia la pila.
Saque G, igual que F.
Saque D, obtenga el nodo hijo H de D y empújelo hacia la pila.
Saque H, igual que F.
Operación de relajación:
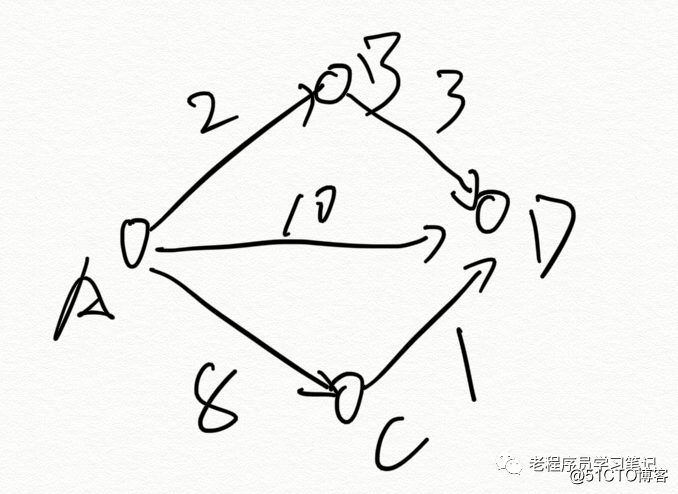
Como se muestra arriba, calcule el camino más corto de A a D.
Al principio, solo sabemos que la ruta de A a A es 0 y la ruta a BCD es desconocida, por lo que la configuramos en ∞.
Calcula la ruta AD como 0 + 10 = 10 <∞, así que cambia D de ∞ a 10. Esta es una operación de relajación.
Algoritmo Bellman-Ford
En pocas palabras, es realizar operaciones de relajación en todos los órdenes y en todos los bordes del gráfico hasta encontrar el camino más corto. Entonces, la complejidad del tiempo debería ser O (número de vértices * número de aristas).
El pseudocódigo debería ser:
for(int i=0;i<顶点数-1;i++){
for(int j=0;j<边数;j++){
松弛操作;
}
}
Sin embargo, en situaciones reales, la ruta más corta se ha encontrado en el recorrido menor que "el número de vértices-1", por lo que una vez finalizado el bucle interno, verifique si hay alguna operación de relajación, de lo contrario, significa que ha sido encontrado Simplemente salte del camino más corto.
Código falso:
for(int i=0;i<顶点数-1;i++){
是否进行了松弛操作=false;
for(int j=0;j<边数;j++){
if(终点权重>起点权重+边权重){
松弛操作:终点权重=起点权重+边权重;终点的起点设为起点名称;
是否进行了松弛操作=true;
}
}
if(没有进行松弛操作){
break;
}
}En combinación con el bucle negativo mencionado anteriormente, luego de ejecutar el número máximo de ciclos de vértices-1, se debe obtener el camino más corto, si volvemos a recorrer todos los bordes, ver si hay alguna operación de relajación. Si es así, significa que hay un bucle negativo.
Agregar pseudocódigo:
是否存在负环路=false;
for(int j=0;j<边数;j++){
if(终点权重>起点权重+边权重){
是否存在负环路=true;
break;
}
}Pasos:
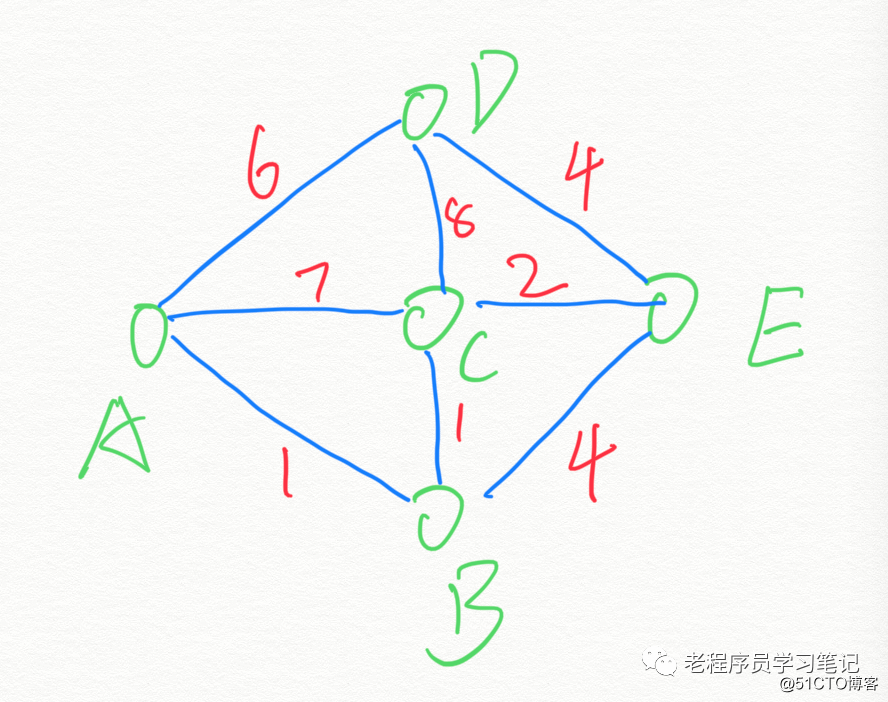
Como se muestra en la figura anterior, hay 5 vértices: ABCDE.
16 bordes (gráfico no dirigido, cada línea representa dos bordes): AB, AC, AD, BA, BC, BE, CA, CB, CD, CE, DA, DC, DE, EB, EC, ED
Usando A como punto de partida, calcule el camino más corto a otros vértices.
En el estado inicial, el peso de A debe ser 0 y todos los demás nodos son ∞.
1. Cambie el peso de AB y B a 1. En este momento, A = 0, B = 1 y el resto son ∞. El punto de partida de B es A.
2. Cambie el peso de AC y C a 7. En este momento, A = 0, B = 1, C = 7. El punto de partida de C es A.
3. Cambie el peso de AD a 6. En este momento, A = 0, B = 1, C = 7, D = 6. El punto de partida de D es A.
4. Trate con BA, BA = 1 + 1 = 2> 0, no se requiere operación de relajación.
5. Procesando BC, BC = 1 + 1 = 2 <7, el peso de C se cambia a 2, en este momento, A = 0, B = 1, C = 2, D = 6. El punto de partida de C se cambia a B.
6. Luego continuar procesando. Esta vez el bucle para todos los bordes, se obtienen los siguientes resultados:
El menor consumo de A a cada punto: A = 0, B = 1, C = 2, D = 6, E = 4
El punto de partida de cada punto: B <- A, C <- B, D <- A, E <- C.
7. Luego comience la siguiente ronda de bucle para todos los bordes En este bucle, no se realiza ninguna operación de relajación, por lo que salta fuera del bucle.
8. Se juzga que no hay bucle negativo y se obtiene el resultado final.