@ @
El concepto
La clasificación de intercambio de vecinos es un algoritmo codicioso común: generaliza la decisión de determinar los dos elementos adyacentes a toda la secuencia para obtener la solución óptima.
Ⅰ: juego de rey P1080
Título Enlace
Título Descripción
Coincide con el Día Nacional de H, el rey invitó a n ministros a jugar un juego de premios. Primero, le pidió a cada ministro que escribiera un número entero en las manos izquierda y derecha, y el propio rey también escribió un número entero en las manos izquierda y derecha. Luego, deja que los n ministros se alineen, y el rey se para al frente de la línea. Después de alinearse, todos los ministros recibirán una cantidad de monedas de oro recompensadas por el rey. La cantidad de monedas de oro recibidas por cada ministro es: el producto del número en la mano izquierda de todos frente al ministro dividido por el número en su mano derecha Luego redondea el resultado.
El rey no quiere que cierto ministro obtenga muchas recompensas, por lo que quiere que lo ayudes a reorganizar el orden del equipo para que el ministro que recibe la mayor cantidad de recompensas reciba la menor cantidad de recompensas posible. Tenga en cuenta que la posición del rey siempre está al frente del equipo.
Formato de entrada:
La primera línea contiene un número entero n, que representa el número de ministros.
La segunda línea contiene dos enteros a y b, separados por un espacio para representar los enteros en las manos izquierda y derecha del rey.
En las siguientes n líneas, cada línea contiene dos enteros a y b, separados por un espacio para representar los enteros en las manos izquierda y derecha de cada ministro.
Formato de salida:
Un número entero que representa el número de monedas de oro recibidas por el ministro más premiado del equipo reorganizado.
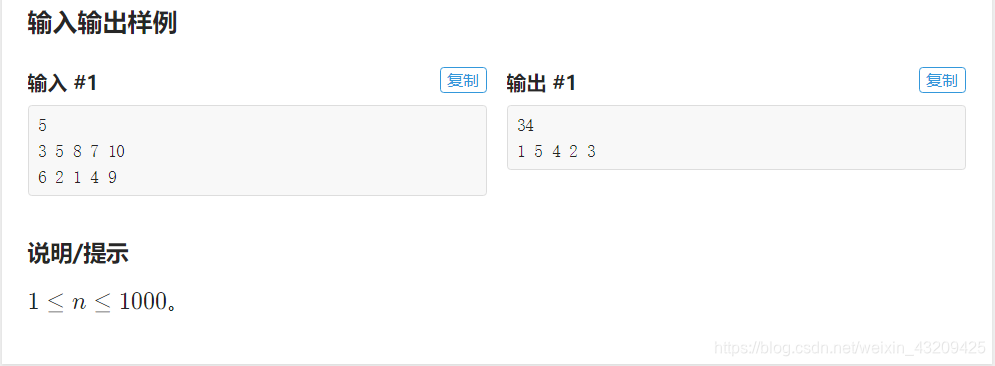
Muestra de entrada n. ° 1:
3
1 1
2 3
7 4
4 6
Muestra de salida n. ° 1:
2
【Rango de datos】
Para el 20% de los datos, 1≤ n≤ 10,0 <a, b <81≤n≤10,0 <a, b <8;
Para el 40% de los datos, 1≤n≤20,0 <a, b <81≤n≤20,0 <a, b <8;
Para el 60% de los datos, 1≤ n≤1001≤n≤100;
Para el 60% de los datos, asegúrese de que la respuesta no exceda 10 ^ 9109;
Para datos del 100%, hay 1 ≤ n ≤1,000,0 <a, b <100001≤n≤1,000,0 <a, b <10000.
Pensamiento
proporcionado i y j son dos Ministro adyacente, en el producto del número de todos siempre delante de ambos ministro izquierda es K , entonces
① Si i a j valor mayor de frente, tanto el Ministro de recompensa
② Si i al j espalda, y luego los dos valores es grande ministro recompensados
Debido a que el valor máximo de los requisitos mínimos significado de problemas, nos propusimos i en el j mejor delantero, en este momento necesita satisfacer
De nuevo
Entonces la fórmula anterior es equivalente a
Luego generalice esta fórmula (decisión) a toda la secuencia, es decir, de acuerdo con este orden de prioridad, entonces la solución final debe ser la solución óptima.
Algunos pueden preguntarse por qué puede ser extendido a toda la secuencia? ¿Qué pasa si i y j no son adyacentes?
Para toda la secuencia, todos los vecinos de la secuencia deben cumplir con la decisión anterior, que es equivalente a ordenar de acuerdo con esta decisión
Si no lo entendemos, simulemoslo. Arriba, hemos demostrado que dos elementos adyacentes deben satisfacer la fórmula anterior para garantizar la solución óptima de estos dos elementos. Primero arreglamos el orden de acuerdo con la decisión anterior. Elementos no adyacentes i y j (suponiendo que j esté detrás de i ), intercambiando elementos en dos posiciones, ya no estará satisfecho
Además ya no está satisfecho
Y
Para la ecuación (1): los elementos de la desigualdad en la primera línea son adyacentes, intercambiamos sus elementos, de modo que se satisfaga la primera línea, y los elementos en la segunda línea son adyacentes, intercambiamos. Hasta que el elemento original en i haya alcanzado la posición de j , y los elementos originales de i a j avancen en uno. En este momento, el orden de intercambio de vecinos satisface completamente (1); lo
mismo es cierto para (2) Ecuación: Los elementos de la desigualdad en la última línea son adyacentes, intercambiamos sus elementos, y luego los elementos en la penúltima línea son adyacentes, y luego intercambian ... hasta que el elemento original en j alcanza la posición i , luego usa el intercambio vecino La clasificación satisface completamente la fórmula (2).
A partir de esto: no hay un orden vecino en toda la secuencia que no satisfaga nuestra decisión.
Las preguntas anteriores parecen haber explicado la esencia del intercambio de vecinos: iniciar la decisión , luego mirar
Ⅱ: P2123 Queen Game
Tema Enlace


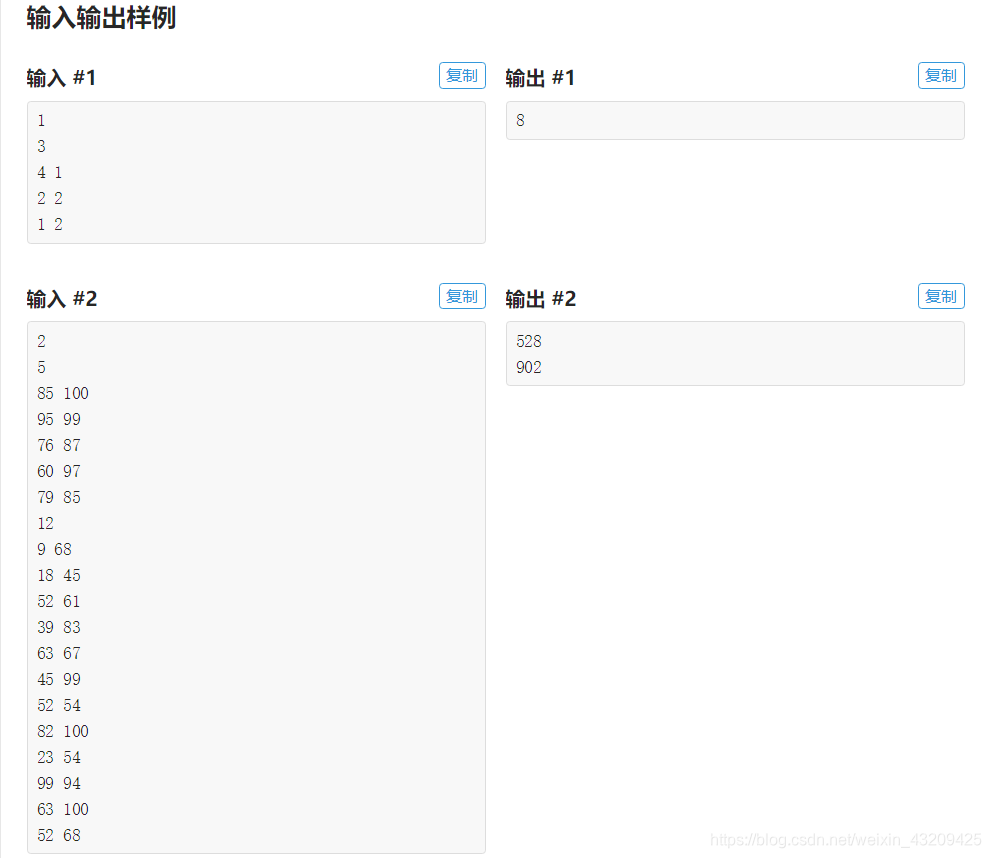

significado de las preguntas, que establece el ministro de i y j adyacente a un ministro de la anterior bonificación dos ministros es C, y el número de los dos ministros anteriores dejaron todos los ministros de la suma, entonces
① si i en j delante, Entonces, el mayor valor de las bonificaciones de los dos ministros es $$ max (max (C, sum + a_ {i}) + b_ {i}, sum + a_ {i} + a_ {j}) + b_ {j} , Que es $$
② Si i a j de nuevo, entonces el ministro dos más grandes valor recompensado $$ max (max (C, suma + a_ {j}) + b_ {j}, suma + a_ {i} + a_ {j }) + b_ {i}, que es $$
El problema es que el valor máximo es el más pequeño, configuramos i para que sea mejor al frente, luego hay
Desarma el máximo dentro, es decir
De los cuales
Eliminar (explicado más tarde por qué se puede eliminar), y luego convertirse
Eliminar suma
Simplifica, consigue
Elemento de cambio
Observe que los números más grandes se eliminan en los lados izquierdo y derecho, dejando lo opuesto a los números más pequeños.
Borrado
Parece que hemos encontrado la decisión final más simple y luego la hemos extendido a toda la secuencia para obtener la solución óptima.
¿Por qué podemos eliminar el mismo término? Podemos simplificar la fórmula anterior para
\ [max (a1, b1, c) \ leqslant max (a2, b2, c) \]Entonces, si c es el mayor de todos los números, entonces los lados izquierdo y derecho son iguales. Es lo mismo si cambias o no.
Si c no es el mayor de todos los números, no te importa la existencia de c, porque solo se determina que esta desigualdad es verdadera. Elementos más grandes que c.
Entonces, puedes eliminar c
Sin embargo, esta decisión es incorrecta. Pero tanto es malo incompleta describir mejor,
la explicación estándar es que debido a que esta decisión no se ajusta a la estricta ordenación débil es no transitiva comparables . Explicamos directamente con un conjunto de datos.
Esto explica qué sencilla transitivo no comparable , es decir, \ (a <= b, b <= c \) no puede liberar \ (A <= \ C) , este caso no se puede generalizar directamente a la secuencia completa la necesidad de añadir algo para satisfacer transitiva no es comparable trabajo.
Sabemos que el conflicto es causado por \ (min (b_ {i}, a_ {j}) = min (b_ {j}, a_ {i}) \) Si los vecinos deben ser intercambiados y ambiguos, y luego analizar las preguntas dadas La fórmula
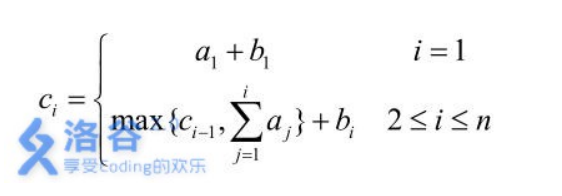
puede encontrar que el prefijo de a tiene una cierta influencia en la respuesta, por lo que cuando son iguales, colocar un pequeño delante será una mejor opción; de manera similar, b también debe tener un efecto en la respuesta, y se calculará cada b Una vez, cuando es igual, es mejor poner b delante de él. Entonces se pueden extraer dos soluciones (es decir, dos decisiones correctas):
================================================== =========
#include<bits/stdc++.h>
using namespace std;
#define I inline
#define rg register
#define ll long long
I ll rd()
{
ll x=0,f=0; char c=getchar();
while(!isdigit(c)){f|=c=='-';c=getchar();}
while( isdigit(c)){x=(x<<3)+(x<<1)+(c-48);c=getchar();}
return f?-x:x;
}
const int N = 2E4+10;
struct node{
ll a,b;
bool operator < (const node& x)const{
return min(a,x.b)==min(x.a,b)?a<x.a:min(a,x.b)<min(x.a,b); //决策 1
return min(a,x.b)==min(x.a,b)?b>x.b:min(a,x.b)<min(x.a,b); //决策 2
}
}e[N];
int n;
int main()
{
int T=rd();
while(T--)
{
n=rd();
for(int i=1;i<=n;i++) e[i].a=rd(),e[i].b=rd();
sort(e+1,e+n+1);
ll sum=e[1].a+e[1].b,pre=e[1].a;
for(int i=2;i<=n;i++)
pre+=e[i].a,sum=max(sum,pre)+e[i].b;
printf("%lld\n",sum);
}
}
Para cada grupo \ ((a_ {i}, b_ {j}) \) la relación entre los dos elementos también afecta la respuesta, tratamos de establecer
Aquí, todos los elementos se dividen en tres categorías, de acuerdo con \ (min (b_ {i}, a_ {j}) \ leqslant min (b_ {j}, a_ {i}) \) para juzgar:
\ (① d_ {i} = d_ {j} = -1, ordenar en orden ascendente de a; \)
\ (② d_ {i} = d_ {j} = 0, organizar aleatoriamente; \)
\ (③ d_ {i} = d_ {j} = 1, en orden descendente de b; \) El \ (d_ {i}! = D_ {j} \)
restante puede satisfacerse siempre que \ (d_ {i} <d_ {j} \) esté satisfecho \ (min (b_ {j}, a_ {i}) \ leqslant min (b_ {i}, a_ {j}) \) , en resumen, la nueva decisión no solo satisface completamente las limitaciones de la decisión anterior, sino que también satisface la transmisión de no comparable (no es difícil encontrar, después de la clasificación de los elementos, cada tipo que tiene una transferencia entre el elemento y que tiene también resistencia a la transferencia entre las clases), de esta manera se obtiene una tercera solución.
================================================== =========
#include<bits/stdc++.h>
using namespace std;
#define I inline
#define rg register
#define ll long long
I ll rd()
{
ll x=0,f=0; char c=getchar();
while(!isdigit(c)){f|=c=='-';c=getchar();}
while( isdigit(c)){x=(x<<3)+(x<<1)+(c-48);c=getchar();}
return f?-x:x;
}
const int N = 2E4+10;
struct node{
ll a,b,d;
bool operator < (const node& x)const{
if(d==x.d)
{
if(d<=0) return a<x.a;
else return b>x.b;
}
return d<x.d;
}
}e[N];
int n;
int main()
{
int T=rd();
while(T--)
{
n=rd();
for(int i=1;i<=n;i++){
e[i].a=rd(),e[i].b=rd();
if(e[i].a<e[i].b) e[i].d=-1;
if(e[i].a==e[i].b) e[i].d=0;
if(e[i].a>e[i].b) e[i].d=1;
}
sort(e+1,e+n+1);
ll sum=e[1].a+e[1].b,pre=e[1].a;
for(int i=2;i<=n;i++)
pre+=e[i].a,sum=max(sum,pre)+e[i].b;
printf("%lld\n",sum);
}
}
Ⅲ: Programación de producción de procesamiento P1248
Análisis: Este es un problema típico de programación de tuberías. Con la idea del intercambio de vecinos, primero asumimos que solo hay dos productos, y el tiempo de procesamiento es \ ((a_ {i}, b_ {i}) y (a_ {j }, B_ {j}) \) , entonces
① Si i a j frontal, el tiempo requerido es \ (a_i + max (A_j, b_i) + b_j \) ;
② si i a j después, el tiempo requerido es \ ( a_j + max (a_i, b_j) + b_i \) ;
Ahora suponemos que el esquema anterior es mejor, y debería haber
Elemento de cambio
Tanto el lado izquierdo como el derecho son equivalentes a dejar un pequeño número opuesto, es decir
Eliminar el signo menos eventualmente
Del mismo modo, esta decisión sin duda no cumple con el paso del no comparables , y la solución como un problema, no repetirlos.
================================================== =========
#include<bits/stdc++.h>
using namespace std;
#define I inline
#define rg register
#define ll long long
I ll rd()
{
ll x=0,f=0; char c=getchar();
while(!isdigit(c)){f|=c=='-';c=getchar();}
while( isdigit(c)){x=(x<<3)+(x<<1)+(c-48);c=getchar();}
return f?-x:x;
}
const int N = 2E4+10;
struct node{
ll a,b,d,id;
bool operator < (const node& x)const{
if(d==x.d)
{
if(d<=0) return a<x.a;
else return b>x.b;
}
return d<x.d;
}
}e[N];
int n;
int main()
{
n=rd();
for(int i=1;i<=n;i++) e[i].a=rd();
for(int i=1;i<=n;i++) e[i].b=rd();
for(int i=1;i<=n;i++){
e[i].id=i;
if(e[i].a<e[i].b) e[i].d=-1;
if(e[i].a==e[i].b) e[i].d=0;
if(e[i].a>e[i].b) e[i].d=1;
}
sort(e+1,e+n+1);
ll sum=e[1].a;
for(int i=2;i<=n;i++)
if(e[i].a>=e[i-1].b) sum+=e[i].a;
else e[i+1].a-=(e[i-1].b-e[i].a),sum+=e[i-1].b;
sum+=e[n].b;
printf("%lld\n",sum);
for(int i=1;i<=n;i++) printf("%d%c",e[i].id,i==n?'\n':' ');
}