Comprensión del algoritmo de Bresenham

Bresenham

Descargo de responsabilidad: el autor de este blog es el mismo que este blog https://blog.csdn.net/cjw_soledad/article/details/78886117, porque la función "Eliminación de blogs" no es efectiva y debe volver a publicarse

El algoritmo de Bresenham es un algoritmo diseñado para la característica de "la pantalla (pantalla o impresora) está compuesta de píxeles" en gráficos de computadora, de modo que todos los puntos en el proceso de encontrar líneas rectas se calculan con números enteros, lo que mejora en gran medida la velocidad de cálculo .

Código de implementación

Este artículo explica principalmente el siguiente código: si puede comprender el siguiente código, puede omitir este artículo.

// 来源:https://rosettacode.org/wiki/Bitmap/Bresenham%27s_line_algorithm#C

void line(int x0, int y0, int x1, int y1) {
 
  int dx = abs(x1-x0), sx = x0<x1 ? 1 : -1;
  int dy = abs(y1-y0), sy = y0<y1 ? 1 : -1; 
  int err = (dx>dy ? dx : -dy)/2, e2;
 
  for(;;){
    setPixel(x0,y0);
    if (x0==x1 && y0==y1) break;
    e2 = err;
    if (e2 >-dx) { err -= dy; x0 += sx; }
    if (e2 < dy) { err += dx; y0 += sy; }
  }
}

Ecuación de línea recta

Como todos sabemos, la ecuación de línea recta más básica con intersección de pendiente es \ (y = kx + b (k es pendiente, b es intersección) \) . La desventaja de esta ecuación es que no puede representar la línea recta \ (x = \ alpha \) , por lo que se usa una nueva ecuación en lugar de \ (Ax + By + C = 0 \) .

Bresenham

El paso principal del algoritmo de Bresenham para dibujar líneas rectas es determinar la posición del siguiente punto. Hay una imagen en Wikipedia para comparar la imagen
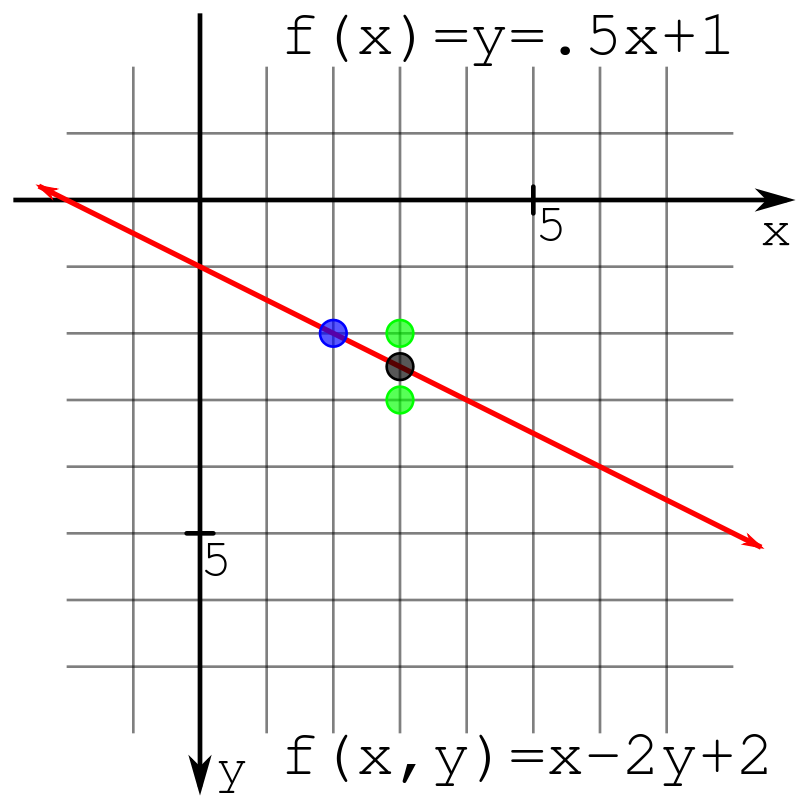
Ilustración de Bresenham
. En la imagen, cada punto representa un píxel . Supongamos que tenemos una línea recta \ (f (x, y) \) y la coordenada actual es \ ((x, y) \) . Los pasos de la coordenada del eje y de un punto son (similares si desea determinar la coordenada del eje x):
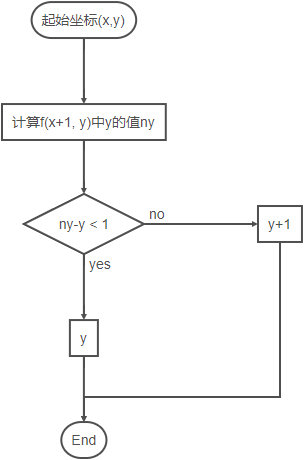
diagrama de flujo

Comprensión del código

Como se mencionó anteriormente, ahora podemos determinar que el siguiente píxel de la línea está allí, pero las ventajas del algoritmo de Bresenham aún no se han manifestado: todavía necesitamos calcular números de coma flotante. Para evitar los cálculos de coma flotante, debemos descubrir la regla de subrayar más profundamente.

Aquí solo consideramos el caso de \ (x_1 <x_2 \) y \ (y_1 <y_2 \) , de hecho, solo necesitamos considerar esta situación, como está escrito en el código anterior sx, sy, a través de estas dos variables podemos controlar el La dirección de la línea dibujada es correcta.

La entrada de Bresenham es dos puntos \ ((x_1, y_1), (x_2, y_2) \) . En base a estos dos puntos, podemos calcular la "distancia" entre los dos puntos. La distancia aquí es un valor absoluto, correspondiente al código dx, dy.

\[\Delta x=|x_1-x_2|\\ \Delta y=|y_1-y_2| \]

De acuerdo con la forma truncada \ (y = kx + b \) , tenemos \ (y = \ frac {\ Delta y} {\ Delta x} x + b \) , y luego

\[\Delta y x-\Delta x y+C = 0 \]

En esta fórmula:

\[x+1 \Rightarrow y+\frac{\Delta y}{\Delta x} \\ y+1 \Rightarrow x +\frac{\Delta x}{\Delta y} \]

De hecho, \ (\ frac {\ Delta y} {\ Delta x} \) y \ (\ frac {\ Delta x} {\ Delta y} \) se usan para juzgar la posición del siguiente punto . El propósito fundamental de estos dos cambios de valor es hacer que la ecuación anterior sea verdadera. De acuerdo con esto, introducimos directamente una variable \ (err \) para evitar la aritmética de coma flotante (correspondiente a la errsuma en el código e2)

\[\Delta y x-\Delta x y+C +err= 0 \\ x+1 \Rightarrow err-\Delta y \\ y+1 \Rightarrow err+\Delta x \]

Ahora hemos podido conectar \ (err \) y \ (x, y \) , pero todavía hay un problema muy importante que no se ha resuelto: determinar si aumentamos la coordenada del eje x o la coordenada del eje y.
Primero supongamos que estamos en la coordenada inicial \ ((x, y) \) , la actual \ (err \) también es correcta, ahora necesitamos juzgar las coordenadas del siguiente punto.
Según el algoritmo tradicional de Bresenham:

\[(x+\frac{\Delta x}{\Delta y})-(x+1)>0 \Rightarrow \Delta x-\Delta y>0 \Rightarrow x+1\\ (y+\frac{\Delta y}{\Delta x})-(y+1)>0 \Rightarrow \Delta y-\Delta x>0\Rightarrow y+1 \]

Prestamos más atención a la parte media y la transformamos con la relación de \ (err \) y \ (\ Delta x, \ Delta y \) mencionadas en el punto anterior.

\[ \Delta x-\Delta y>0 \Rightarrow -\Delta y>-\Delta x\\ \Delta y-\Delta x>0\Rightarrow +\Delta x < \Delta y \]

De la fórmula anterior, parece que tiene algo que ver con \ (err \) , pero no está claro, es porque nuestro empuje se basa en el punto de partida, si la base no es el punto de partida, entonces la fórmula debería ser

\ [\ Delta x- \ Delta y> 0 \ Rightarrow \ varepsilon - \ Delta y> - \ Delta x \\ \ Delta y- \ Delta x> 0 \ Rightarrow \ varepsilon + \ Delta x <\ Delta y \]

\ (\ varepsilon \) es un valor acumulado, su fuente está relacionada con la posición relativa del punto actual \ ((x, y) \) y el punto de partida \ ((x_0, y_0) \) , la comprensión personal es: cada vez \ ( x + 1 \) o \ (y + 1 \) harán que la línea recta original se traduzca. Esta traducción causará un error, y este error continuará acumulándose a medida que el programa progresa, y este valor acumulado corresponde a \ ( err \)

Ahora tenemos la capacidad de conectar \ (err \) con el programa err.
ifLa última condición corresponde a la fórmula anterior, pero es errdiferente de \ (\ varepsilon \) . La diferencia es: ya errestá calculado \ (\ varepsilon- \ Delta y \) y \ (\ varepsilon + \ Delta x \) . Podemos pensar de esta manera: en cierto punto \ ((x, y) \) , hemos calculado la correcta \ (err \) que puede usarse para juzgar . Cuando elegimos el siguiente punto, podemos pasar por Se calcula el siguiente punto \ (err \) , que es lo que err -= dy; err += dx;implica el código .

if (e2 >-dx) { err -= dy; x0 += sx; }
if (e2 < dy) { err += dx; y0 += sy; }

Sobre la errinicialización en 2020

Notamos que el código fue errinicializado. En frente de la derivación que daba a una parte: el punto de partida \ ((x 1, y1) \ ) El \ (ERR \) . De la fórmula \ (Ax + By + C + err = 0 \) , el punto de partida de \ (err \) debe ser \ (0 \) , pero el código se inicializó con un valor extraño. Parece que los dos son contradictorios, pero errla inicialización es en realidad otro truco.

int err = (dx>dy ? dx : -dy)/2

Mirando hacia atrás a la imagen mencionada anteriormente, el punto azul es el punto de partida. Si el juicio se realiza manualmente, decidiremos dónde está el siguiente punto en función de la ubicación del punto negro . Cuando \ (negro> 0.5 \) , elegiremos el punto verde a continuación, de lo contrario, elegiremos el punto verde arriba.
Ilustración de Bresenham

Sin embargo, aquí se 0.5introducirá la aritmética de coma flotante . Tenemos otra opción: mover el punto de inicio \ ((x_1, y_1) \) hacia arriba media unidad (aquí solo se considera \ (\ Delta x> \ Delta y \) , el resto es el mismo). Debido a que el punto de partida está desplazado desde el primer píxel, se introduce un error \ (err \) . De acuerdo con la derivación previa de \ (err \) :

\ [x_1 + 0.5 \ Rightarrow err- \ Delta y / 2 \\ y_1 + 0.5 \ Rightarrow err + \ Delta x / 2 \]

Esto puede explicar errel problema del valor inicial, y es consistente con nuestra derivación previa.

En este punto, se entiende el algoritmo de Bresenham.