Divide and Conquer: polynomial multiplication, fast Fourier transform

The polynomial representation, such as A (X) = 3x ² + 2x +. 1

Coefficient representation

Composed by the coefficient vector a = (3,2,0)
ie = A (A ₀ , A _{. 1} , ..., A _{n--. 1} )

Point value notation

{(0,1), (1,6), (2,17)}
i.e. {(X ₀ , Y ₀ ), (X _{. 1} , Y _{. 1} ), ..., (X _{n--. 1} , Y _{n--. 1} ) } where Y _K = A (X _K )

Coefficient indicates how to find the point value of said evaluation referred to

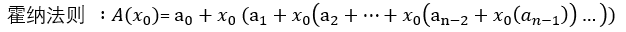
how to find the point value of the coefficient represents represent, called interpolation

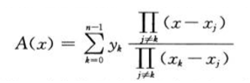
A method of finding also common to both,
if X ₀ ~ X _{n--. 1} different from each other, then M is reversible, we can say the evaluation process is to multiply M, then the interpolation process is multiplied by M ^-1 , Van der Monde matrix inversion is to be faster than the other

Polynomial multiplication
A (x) * B (x ) if the factor that the use of

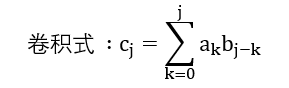
Thus the two paths polynomial multiplication occurs

This is not the time is long, complicated process yet?
As long as the seemingly impassable road improvements can be better, improvements are as follows

1. Evaluation: Note that we need to double the number of community through high-order coefficient is 0 if n coefficients, and then use the FFT (Fast Fourier Transform) seeking point value
2. Pointwise multiplication: C (x) = A (x) B (x)
3. Interpolation: calculating an inverse DFT

---

Well finished above the entry, highlight came

FFT

During our evaluation formula that alterations to
a polynomial, can be turned into the form

that we avoid double counting, we will take the value of the number of pairs of opposite it, such as a number n, we take
± X ₀ , ± X ₁ , ..., the X-± _{the n-/ 2-1}

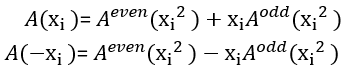
if you noticed it? ! Here is a clever enchant to become the n n / 2 points in A ^{the even} (X) and A ^ODD (X) calculation process (point taken as positive and negative), and the number of times cut in half (Observation A ^{the even} (x) and A ^ODD (x) is easy to see)

This time we naturally think of divide and conquer, then the following recursive solution A ^{the even} (the X-) and A ^{the ODD} (the X-), FFT algorithm do so yet? Of course, also came close distance, we carefully look at the following

在第一次递归中，我们我取值，是n对相反数，可是到了下面递归，平方和平方怎么可能是相反数！！！我们该怎么办？车到山前必有路，大家能想到复数吗？对没有错，我们这次就要使用复数

是不是很神奇，这次我们找到了7次的8个取值，那假如换成15次的呢，我们又应该怎么找呢？头疼，这里是有规律的！
其实上面的8个取值，是z⁸的8个复数根
那么16个就是zⁿ的n个复数根，怎么样想到了吗，哈哈没有错 ，取n个就是zⁿ的n个复数根【这里我就不在讲述n次单位复数根】

终于我们可以n次单位复数根借助复数使用分治算法，来求得点值表示了，这也就是快速傅里叶变换，摘自《算法概论》的伪代码

好了，让我们来总结一下，到底什么是快速傅里叶变换(FFT)以及大家所说的离散傅里叶变换(DFT)

下面是《算法导论》对于DFT的描述

也就是说在n个n次单位复数根处求值过程就是DFT

依照上面的算法所需时间θ(n²)，然而我们使用FFT，利用复数单位根的性质，可以在θ(nlgn)时间内计算出DFT_n(a)，这里我们使用的是分治法递归思路，DFT的实际应用比如信号处理中需要尽可能快的速度，下面介绍一种更加高效的FFT实现，也就是迭代实现，再把《算法导论》的贴上去，大家可以对比一下

---

< 值 > = FFT (< 系数 > , point )

插值

很巧的是

< 系数 > = (1/n) FFT (< 值 > , point^-1 )

这里还是要说明原因的，再把上面的范德蒙德拿下来看