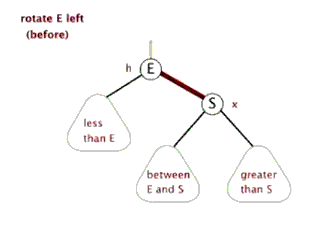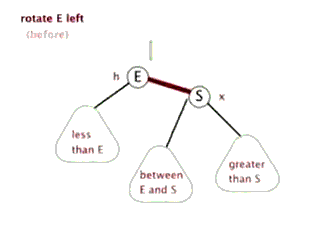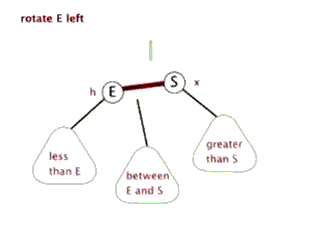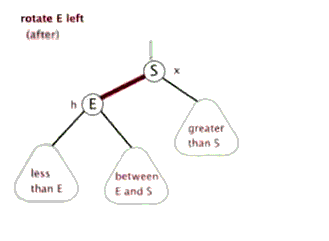
First, the basic concept
AVL tree is also called balanced binary tree, which is either an empty tree, or with the following properties binary sort tree: the absolute value of the difference between the height of its left subtree and left subtree (equilibrium factor) is not more than 1, and its left subtree and right subtree is a balanced binary tree.
Second, the structure
As the basic concept tree having a left subtree and a left subtree, and for any one sub-tree, the left and right subtree subtree're just height does not exceed 1.
2.1 balanced binary tree discriminant
As there are three trees, under which each judge is balanced binary tree?
figure 1:

figure 2:

image 3:

Figure it, it is clear that a height difference can be seen in FIG. 1 are any sub-tree does not exceed 1,
Figure II, the height of the left subtree of node 25 is three, and the height of the right subtree is 5, a height difference of more than 1; for node 32, the height of the left subtree is 3, is a right subtree of height, has a height difference exceed 1, so that the tree is not balanced binary tree.
Figure III, the node 25 is the height of the left subtree 3, and 5 is the right subtree of height, the height difference exceeds one, not a balanced binary tree.
From the chart these cases, should be able to understand what it is a balanced binary tree.
First, a balanced binary tree is a binary search tree, which followed about each sub-tree of height difference is not more than one.
Third, insert Detailed
For a balanced binary tree, when it leads to the insertion of a new value is not balanced binary tree, and how to do this?
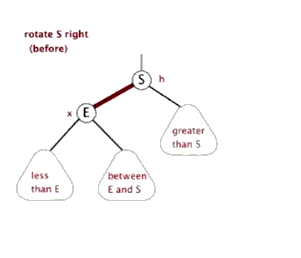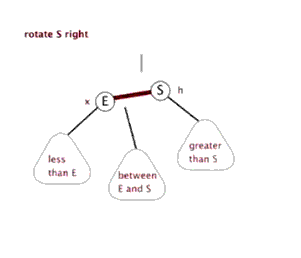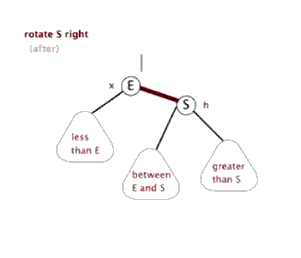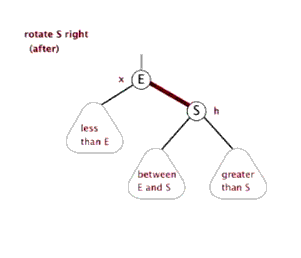
Before inserting the new value:

After inserting the new value:
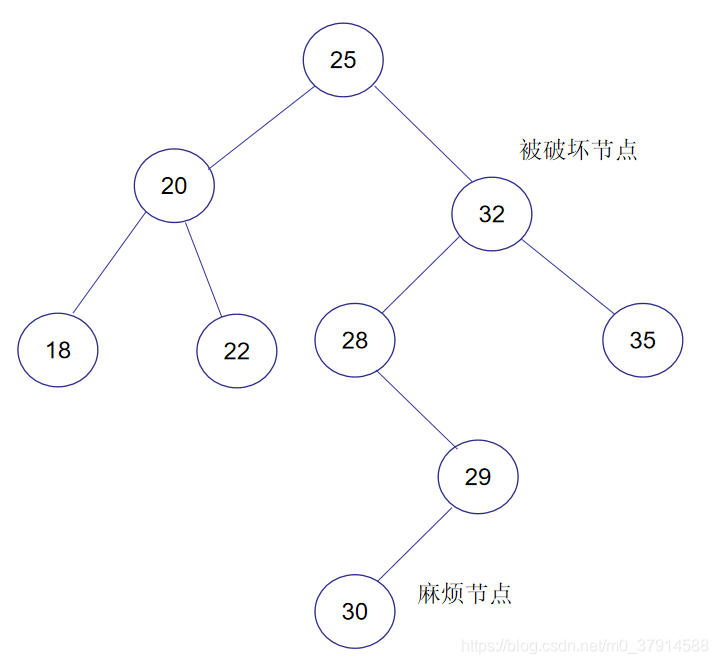
As shown above, this is balanced, if I insert a new node value is 30, then the balance of the tree will be destroyed, it destroys the balance of the total node 32 and node 25, although the two destroyed balance node, but we only discuss recent destruction of the balance of nodes (as well under the deal, the node balance above will also handle), that the newly inserted node 30 destroy the balance of the node 32, because the new node is inserted into the node which led to the destruction of the balance trouble, also known as nodes, are called nodes destroyed undermine the balance of its nodes.
The results and experiences of all, the total destruction of the balance type into four types, namely, LL-type, RR type, LR type and RL-type (L = left, R = right).
3.1 LL型
figure 1:

figure 2:

image 3:

FIG above, LL-type and a type or so, to the left of the left node destruction caused by imbalance inserted, was LL type noted above in FIG. 3, the black line represents the path model determines that it determines all models only times from start determination node is destroyed, i.e., whether you third node newly inserted position in the left or right, as shown in FIGS. 2 and 3, a left and a right but are LL-type, as determined only twice.
LL型解决方案:以被破坏节点为基础进行右旋
3.2 右旋
什么是右旋,根据某个节点向右旋转,只需要记住下面这个图即可,至于右旋为什么能解决LL型问题,其实这是一个经验总结(就像99乘法表),只需要记住即可,后面会总结一个记录方法。
图1右旋:

以25为基础进行进行右旋后结果如下,可以看出,该树处于平衡状态。

图2右旋:

以25为基础进行进行右旋后结果如下,可以看出,该树处于平衡状态。

图3右旋:

以25为基础进行进行右旋后结果如下,可以看出,该树处于平衡状态。

3.3 RR型
图1:

图2:

图3:

如上图,RR型也为右右型,在被破坏节点的右边的右边插入而导致失衡,则为RR型,注意上面3个图,黑色的线表示它型号判断的路径,与LL型相反。
LL型解决方案:以被破坏节点为基础进行左旋
3.4 左旋
什么是左旋,根据某个节点向左旋转,只需要记住下面这个图即可,与右旋相反。
图1左旋:

以20为基础进行进行左旋后结果如下,可以看出,该树处于平衡状态。

图2左旋:

以20为基础进行进行左旋后结果如下,可以看出,该树处于平衡状态。

图3左旋:

以20为基础进行进行左旋后结果如下,可以看出,该树处于平衡状态。

注意:因为左旋、右旋是基础,所以写了3个例子,为了避免文章过于啰嗦,下面RL型和LR型只举一个例子。
3.5 LR型
如图:

如上图,LR型也为左右型,在被破坏节点的左边的右边插入而导致失衡,则为LR型,注意上图,黑色的线表示它型号判断的路径。
LR型解决方案:以被破坏节点L(左)节点为基础先进行一次L(左)旋,再以被破坏节点为基础进行右旋。
上图调整:
先以20为基础进行一次左旋。

再以25为基础进行一次右旋,可以看出经过两次旋转后,该树已经平衡。

3.5 RL型
如图:
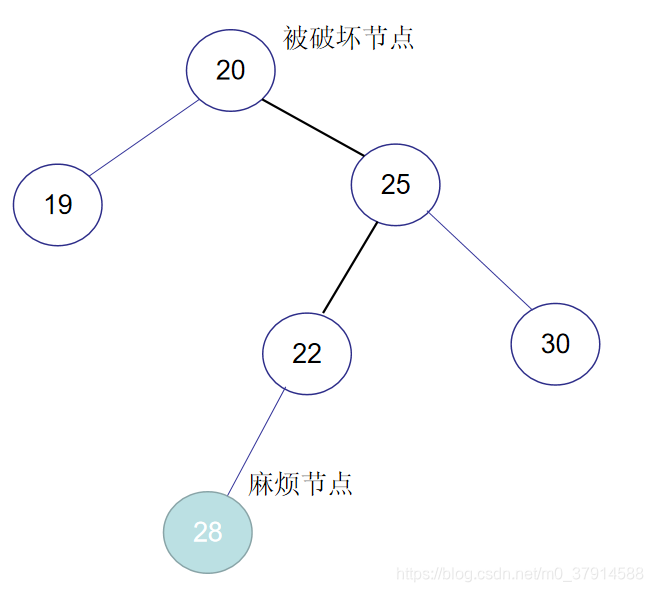
如上图,RL型也为右左型,在被破坏节点的右边的左边插入而导致失衡,则为RL型,注意上图,黑色的线表示它型号判断的路径。
RL型解决方案:以被破坏节点R(右)节点为基础先进行一次R(右)旋,再以被破坏节点为基础进行左旋。
上图调整:
先以25为基础进行一次右旋。

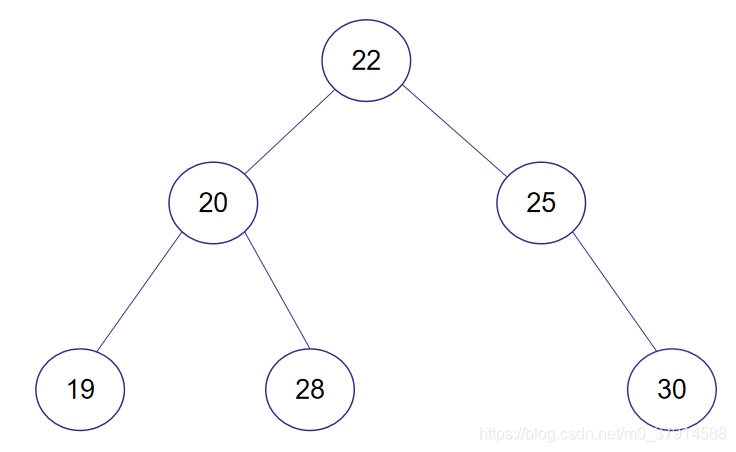
再以20为基础进行一次右旋,可以看出经过两次旋转后,该树已经平衡。
3.6 总结
型号的判断永远是根据被破坏节点到麻烦节点的路径方向来判断,并且只判断两次即可,第三次不管。
处理方式分类两大类:
1.RR型和LL型,以被破坏节点为基础进行其反向的旋转即可,即RR型进行左旋,LL型进行右旋。
2.RL型和LR型,先以被破坏节点的LR或RL首字母的节点进行LR或RL首字母旋转,再以被破坏节点为基础进行LR或RL尾字母旋转,即RL型先以被破坏节点的R(右)节点为基础进行一次R(右)选,再以被破坏节点为基础进行一次L(左)旋;LR旋先以被破坏节点的L(左)节点为基础进行一次L(左)选,再以被破坏节点为基础进行一次R(右)旋。
总结内容,背下即可。
四、删除详解
在第三部分已经对插入进行了详解,其实平衡二叉树的删除比插入更复杂,但也是分为大致六类(其实是三类,左右对称)。
因为平衡二叉树也是一颗二叉查找树,它是在二叉查找树的删除的基础上添加了平衡调整的内容,对于二叉树删除的操作,本文不再概括,如果有对二叉树删除不了解的,可以看我上一篇关于二叉查找树详解博文,本文对于平衡二叉树的删除着重于平衡性的判断和调整。
删除的节点在右子树:
即在右边删除而导致树失衡,此时左子树高度会大于右子树,右子树删除有三种调节方式。
注意:在右子树进行删除一个节点而导致失衡,则相当于在左子树插入一个新节点而导致的失衡,所以需要进行平衡性调整应该从左子树入手。
第一种:删除后被破坏节点的左节点的左边高度大于右边高度。
如图:

删除节点30后,被破坏节点的左节点,即节点20,它左边高度为1,而右边高度为0.。则相当于在节点20的左边插入一个节点18而导致的不平衡,此时即为LL型,进行右旋即可。
相当于下图:

右旋后如图,可以看出已经平衡。

第一种结论:当在右子树删除而导致树失衡时,判断被破坏节点的左节点的左边高度和右边高度,如果左边高度大于右边高度,则相当于在被破坏节点的左节点的左节点下插入一个新的节点而导致的不平衡,即LL型插入,此时进行右旋调整即可。
第二种:删除后被破坏节点的左节点的左边高度小于右边高度。
如图:

删除节点30后,被破坏节点的左节点,即节点20,它左边高度为0,而右边高度为1.。则相当于在节点20的右边插入一个节点22而导致的不平衡,此时即为LR型,先对被破坏节点的L(左)节点进行L(左)旋,再对被破坏节点进行R(右)旋即可。
相当于下图:

先以20为基础进行左旋,再以25为基础进行右旋后如下图,可以看出已经平衡。

第二种结论:当在右子树删除而导致树失衡时,判断被破坏节点的左节点的左边高度和右边高度,如果左边高度小于右边高度,则相当于在被破坏节点的左节点的右节点下插入一个新的节点而导致的不平衡,即LR型插入,此时先对被破坏节点的L(左)节点进行L(左)旋,再对被破坏节点进行R(右)旋即可。
第三种:删除后被破坏节点的左节点的左边高度等于右边高度。
如图:

删除节点30后,被破坏节点的左节点,即节点20,它左边高度为1,而右边高度为1,高度相等,因为在右子树进行删除,此时对被破坏节点进行右旋即可,此种情况背下即可。
以25为基础进行右旋,如下图,可以看出已经平衡。

第三种结论:当在右子树删除而导致树失衡时,判断被破坏节点的左节点的左边高度和右边高度,如果左边高度等于右边高度,因为在右子树进行删除,此时对被破坏节点进行右旋即可。
删除的节点在左子树:
即在左边删除而导致树失衡,此时右子树高度会大于左子树,左子树删除有三种调节方式。
注意:在左子树进行删除一个节点而导致失衡,则相当于在右子树插入一个新节点而导致的失衡,所以需要进行平衡性调整应该从右子树入手。
第一种:删除后被破坏节点的左节点的左边高度小于右边高度。
如图:

删除节点18后,被破坏节点的右节点,即节点25,它左边高度为0,而右边高度为1.。则相当于在节点25的右边插入一个节点30而导致的不平衡,此时即为RR型,进行左旋即可。
相当于下图:

右旋后如图,可以看出已经平衡。

第一种结论:当在左子树删除而导致树失衡时,判断被破坏节点的右节点的左边高度和右边高度,如果左边高度小于右边高度,则相当于在被破坏节点的右节点的右节点下插入一个新的节点而导致的不平衡,即RR型插入,此时进行左旋调整即可。
第二种:删除后被破坏节点的左节点的左边高度大于右边高度。
如图:

删除节点18后,被破坏节点的右节点,即节点25,它左边高度为1,而右边高度为0。则相当于在节点25的左边插入一个节点23而导致的不平衡,相当于RL型插入,此时先对被破坏节点的R(右)节点进行R(右)旋,再对被破坏节点进行L(左)旋即可。
相当于下图:

先以25为基础进行右旋,再以20为基础进行左旋后如下图,可以看出已经平衡。

第二种结论:当在左子树删除而导致树失衡时,判断被破坏节点的右节点的左边高度和右边高度,如果左边高度大于右边高度,则相当于在被破坏节点的右节点的左节点下插入一个新的节点而导致的不平衡,即RL型插入,此时先对被破坏节点的R(右)节点进行R(旋)旋,再对被破坏节点进行L(左)旋即可。
第三种:删除后被破坏节点的左节点的左边高度等于右边高度。
如图:

删除节点18后,被破坏节点的右节点,即节点25,它左边高度为1,而右边高度为1,因为在左子树进行删除,此时对被破坏节点进行左旋即可,此种情况背下即可。
以20为基础进行左旋,如下图,可以看出已经平衡。

第三种结论:当在左子树删除而导致树失衡时,判断被破坏节点的左节点的左边高度和右边高度,如果左边高度等于右边高度,因为在左子树进行删除,此时对被破坏节点进行左旋即可。
结论:
在某一边删除而导致失衡时,则判断被破坏节点的某节点的左右高度,如果高度不一致,则相当于在某边+高度高的那一边进行的插入,根据类型判断对应的旋转;如果高度一致,则对被破坏节点进行删除某旋即可。
注意:某代表左或右,如果在左边删除则为左。
五、遍历概括
平衡二叉树的遍历和二叉搜索树的遍历是一致的,请看上一篇博文的遍历描述即可。