Description: "Mathematical Analysis principle" refers to г.м. 菲赫金哥尔茨 the "principle of mathematical analysis" (vol Ninth Edition) Higher Education Press
Collectively referred to as whole and fractional rational number. Rational Field can not fully meet the needs of a mathematical definition, it can not be such a length of the diagonal of a square of 1 represents a rational number, i.e., not a rational number which is equal to the square of the energy of 2 $ {\ frac {{p} } {{q}}} $ ( $ {p} $ and $ {q} $ are two natural number) exists (Note that the natural numbers corresponding to the original book we said positive integer). The following record book by contradiction to prove this conclusion process.
Proof 1
Argument: a square it is not a rational number can be equal to $ 2 {\ frac {{p}} {{q}}} $ ($ {p} $ and $ {q} $ is a natural number of two) is present
Proof: reductio ad absurdum
Proof: Assuming the fraction is $ {\ frac {{p}} {{q}}} $ exists, such that $ {{\ left ({\ frac {{p}} {{q}}} \ right)} \ mathop {{}} \ nolimits ^ {{2}} \ text {} = \ text {} 2} $. This score can be assumed is irreducible, i.e. $ {p} $ $ {q} $ with no common factor, no longer approximately minutes. By $ {p \ mathop {{}} \ nolimits ^ {{2}} \ text {} = \ text {} 2q \ mathop {{}} \ nolimits ^ {{2}}} $, so $ {p} $ is even. By $ {\ frac {{p}} {{q}}} $ irreducible, so $ {q} $ is an odd number. Provided $ {p = 2r} $ ($ {r} $ is an integer), there is $ {p \ mathop {{}} \ nolimits ^ {{2}} \ text {} = \ text {} 2q \ mathop { {}} \ nolimits ^ {{2}} \ text {} = \ text {} 4r \ mathop {{}} \ nolimits ^ {{2}}} $, further $ {q \ mathop {{}} \ nolimits ^ {{2}} \ text {} = \ text {} 2r \ mathop {{}} \ nolimits ^ {{2}}} $, whereby push $ {q} $ is an even number, and this hypothesis contradictory, argument is proved.
Lack of Rational Field in geometry simply expressed as " not all segments can have length ." For example, the above-described square side length of a square whose diagonal length of 1 to 2, but can not be represented by a diagonal length of rational itself, which can be derived an argument.
The book expand the domain of rational numbers, irrational numbers is defined by the German mathematician Dedekind record rational discussion within segmentation concept drawn. Consider all rational numbers into two non-empty set $ {A} $ and $ {A '} $, assuming:
1. Each rational numbers but only $ {A} $ or $ {A '} $ a set of two
2. A $ every number set in less than a set {a} $ $ {A '} $ $ every number in {a'} $
Two conditions are met for Rational Field FRACTIONMETHOD called "segmentation." Wherein the set $ {A} $ called the divided lower class , set A 'is called on a class , dividing the available $ {A | A'} $ Fig. The book proves that division can only have the following three types:
1) the lower class $ {A} $ is not the maximum number, and that has the least number of $ $ {a} on the class $ {A} $;
2) the lower class $ {A '} $ has the largest number of $ {r} $, {A} $ but not the smallest number in the class $;
3) both the lower class is not the maximum number, and not the smallest number in the class.
The first two divided by $ {r} $ rational number generated ($ {r} $ $ {A} $ is the $ {A '} $ Bounded two intermediate), or that which defines the rational division $ {r} $. Number Bounds third case there is no rational domain, division can not define any rational number, and therefore the introduction of an irrational number, and the provisions of any 3) is divided is of the type defined in any one of irrational number $ {[alpha]} $ , $ {[alpha]} $ this will replace the missing number of circles.
Following is a brief case diagrammatically represented by three, and the third case proved.
Division one:
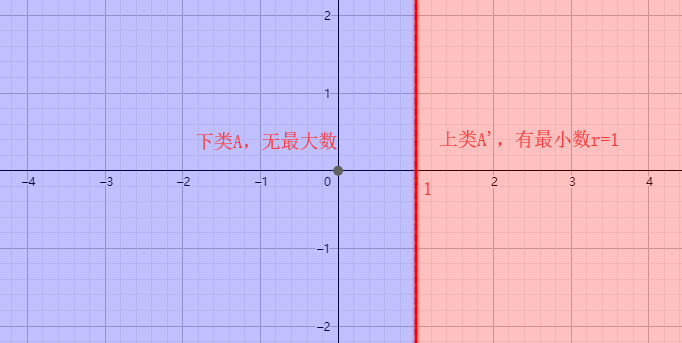
Segmentation II:
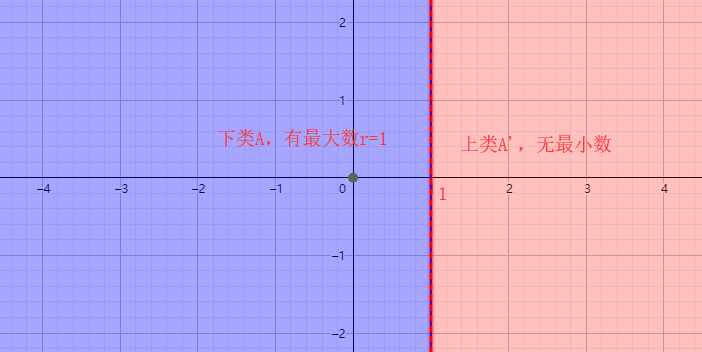
Division three:
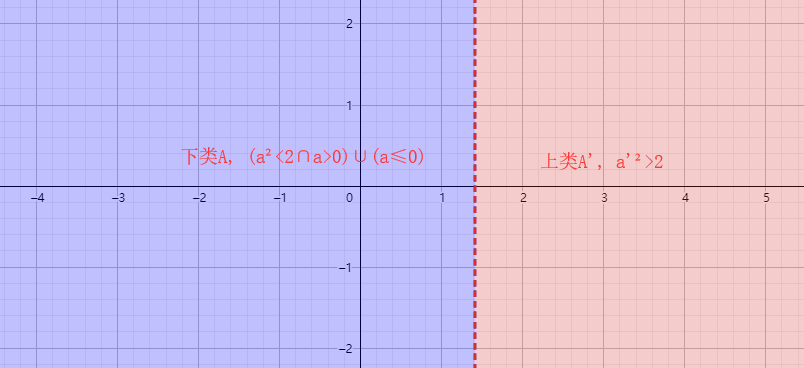
The following record book to prove the divided three first case, the second case to prove the method then modeled.
Proof 2
Argument: the rational domain, everything that the $ {a \ mathop {{}} \ nolimits ^ {{2}} \ text {} <\ text {} 2} $ positive rational number $ {a} $, $ {0 } $ rational and all are included in a negative $ {a} $ type, so that all the $ {\ mathop {{a '}} \ nolimits ^ {{2}} \ text {}> \ text {} 2} $ of positive rational number $ {a '} $ fall $ {A'} $ type, prove $ {A} $ category is neither the maximum number, the $ {A '} $ no minimum number of classes.
Proof: scaling method to prove inequality
prove:
(1). 首先,证明在 ${A}$ 类中无最大数
我们只需显示证明 ${a\mathop{{}}\nolimits^{{2}}\text{ } < \text{ }2}$ 的情况,${a\mathop{{}}\nolimits^{{2}}\text{ } \le \text{ }0}$ 的情况很明显成立。
设 ${a}$ 是 ${A}$ 类中的任一整数,则有${a\mathop{{}}\nolimits^{{2}} < 2}$,我们需证明如果可以有正数${n}$,使得
${{ \left( {a+\frac{{1}}{{n}}} \right) }\mathop{{}}\nolimits^{{2}}\text{ } < \text{ }2}$ (1),
也就是说让 ${a+\frac{{1}}{{n}}}$ 也属于${A}$类。展开不等式并移项可得
${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }2-a\mathop{{}}\nolimits^{{2}}}$ (2)
又对于正数${n}$,不妨取 ${n > 1}$,则有
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }}\frac{{1}}{{n}}$
不等式两边同时加正数 ${\frac{{2a}}{{n}}}$ 可得
${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }\frac{{2a}}{{n}}+\frac{{1}}{{n}}}$
亦即 ${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }\frac{{2a\text{ }+1}}{{n}}}$
如果 ${n}$ 满足不等式 ${{\frac{{2a\text{ }+1}}{{n}}}\text{ } < \text{ }2-a\mathop{{}}\nolimits^{{2}}}$ ,则不等式成立 (2) 成立,进而不等式 (1) 成立。为此,只要取
${n\text{ } > \text{ }\frac{{2a+1}}{{2-a\mathop{{}}\nolimits^{{2}}}}}$
即可。由此可见,无论 ${a}$ 是 ${A}$ 类中怎样的一个正数,在 ${A}$ 类中总能找到大于 ${a}$ 的数。联系 ${a\mathop{{}}\nolimits^{{2}}\text{ } \le \text{ }0}$ 的情况,在 ${A}$ 类中无最大数得证。
(2). 同理,证明在${A'}$类中无最小数
设 ${a'}$ 是 ${A'}$ 类中的任一整数,则有 ${\mathop{{a'}}\nolimits^{{2}}\text{ } > \text{ }2}$。我们需证明如果可以有正数 ${n}$ 使得
${{ \left( {a'-\frac{{1}}{{n}}} \right) }\mathop{{}}\nolimits^{{2}}\text{ } > \text{ }2}$ (3)
也就是说让 ${a'-\frac{{1}}{{n}}}$ 也属于 ${A'}$ 类。展开不等式 (3) 并移项可得:
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ }-\text{ }\frac{{2a'}}{{n}}\text{ } > \text{ }2\text{ }-\text{ }a'\mathop{{}}\nolimits^{{2}}}$ (4)
对于正数 ${n}$,取 ${0 < n < 1}$,则有
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } > \text{ }\frac{{1}}{{n}}}$
不等式两边同时减去 ${\frac{{2a'}}{{n}}}$ 可得
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ }-\text{ }\frac{{2a'}}{{n}}\text{ } > \text{ }\frac{{1}}{{n}}\text{ }-\text{ }\frac{{2a'}}{{n}}}$
亦即 ${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ }-\text{ }\frac{{2a'}}{{n}}\text{ } > \text{ }\frac{{1-2a'}}{{n}}}$
如果 ${n}$ 满足不等式 ${\frac{{1-2a'}}{{n}}\text{ } > \text{ }2\text{ }-\text{ }a'\mathop{{}}\nolimits^{{2}}}$,则不等式 (4) 成立,进而不等式 (3) 成立。
为此,只要取
${n\text{ } < \text{ }\frac{{1-2a'}}{{a'\mathop{{}}\nolimits^{{2}}-2}}}$
即可。由此,无论${a'}$ 是 ${A'}$ 类中怎样的一个正数,在 ${A'}$ 类中总能找到小于 ${a'}$ 的数。故,在 ${A'}$ 类中无最小数得证。
分割三在有理数域不存在界数,但可以在无理数域找到这个界数就是 ${{\sqrt{{2}}}}$。
事实上,在引进了无理数后,前述三种分割也可以统一起来。这建立在一下两个规定之上:
(1). 有理数和无理数统称为实数
(2). 将界数归到上类
这样,在实数域内定义的分割就是:
在下类 ${A}$ 中没有最大的数,而在上类 ${A'}$ 中有最小的数 ${r}$ 。