[C++ Grocery Store] A juggling binary search tree——AVLTree

Insert image description here

Article directory

I. Introduction
2. The concept of AVL tree
3. Definition of AVL tree nodes
4. AVL tree framework
5. Insertion of AVL tree
6. Deletion of AVL tree
7. Performance of AVL tree
8. Conclusion

I. Introduction

In the previous article, I gave a brief introduction to set, multiset, map, and multimap. In the introduction of the documentation, I found that these containers have one thing in common: their bottom layers are all implemented with the help of binary search trees. However, the binary search tree has its own shortcomings. If the elements inserted into the tree are ordered or nearly ordered, the binary search tree will degenerate into a single branch tree, and the time complexity will degenerate into O ( N ) O ( $O (N)$ , so the underlying structure of associative containers such as set and map is a balanced binary tree, that is, a balanced tree is used to implement it. So today let us take a closer look at the underlying structure of set and map.

2. The concept of AVL tree

Although the binary search tree can shorten the search efficiency, if the data is ordered or close to ordered, the binary search tree will degenerate into a single branch tree. Searching for elements is equivalent to searching for elements in the sequence table, and the efficiency will become low. Therefore, two Russian mathematicians GMAdelson-Velskii and EMLandis invented a method to solve the above problem in 1962: after inserting a new node into the binary search tree, if the height of the left and right subtrees of each node can be guaranteed to be If the absolute value of the difference does not exceed 1 (more than 1, the nodes in the tree need to be adjusted), the height of the tree can be reduced, thereby reducing the average search length. An AVL tree is either an empty tree or a binary search tree with the following properties:

Its left and right subtrees are both AVL trees.
The absolute value of the difference between the heights of the left and right subtrees (referred to as the balance factor) does not exceed 1 (-1, 0, 1).

Insert image description here
Small Tips : If a binary search tree is of average height, it is an AVL tree. If it has n nodes, its height can be maintained at $O(log2^n)$ , the search time complexity is $O(log2^n)$ . Balance in a balanced binary search tree does not mean that the balance factor should always remain 0. This is impossible. Taking two nodes as an example, the balance factor of the root node can only be 1 or -1, and cannot be 0. . It is basically impossible for a binary search tree to achieve complete balance in practice, but in theory it can, that is, a full binary tree. The multi-fork balanced search tree we learned later can be completely balanced in reality.

3. Definition of AVL tree nodes

template<class K, class V>
struct AVLTreeNode
{
    
    
	AVLTreeNode(const pair<K, V>& kv = pair<K, V>())
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_bf(0)
	{
    
    }

	pair<K, V> _kv;//存储key和value
	AVLTreeNode<K, V>* _left = nullptr;//指向左孩子
	AVLTreeNode<K, V>* _right = nullptr;//指向右孩子
	AVLTreeNode<K, V>* _parent = nullptr;//指向父亲结点
	int _bf = 0;//平衡因子
};

4. AVL tree framework

template<class K, class V>
	class AVLTree
	{
    
    
		typedef AVLTreeNode<K, V> Node;
	private:
		Node* _root = nullptr;
	};

5. Insertion of AVL tree

The AVL tree introduces a balance factor based on the binary search tree, so the AVL tree can also be regarded as a binary search tree. Then the insertion process of AVL tree can be divided into two steps:

Insert new nodes as in a binary search tree.
Adjust the node's balance factor.

5.1 Update of balance factors

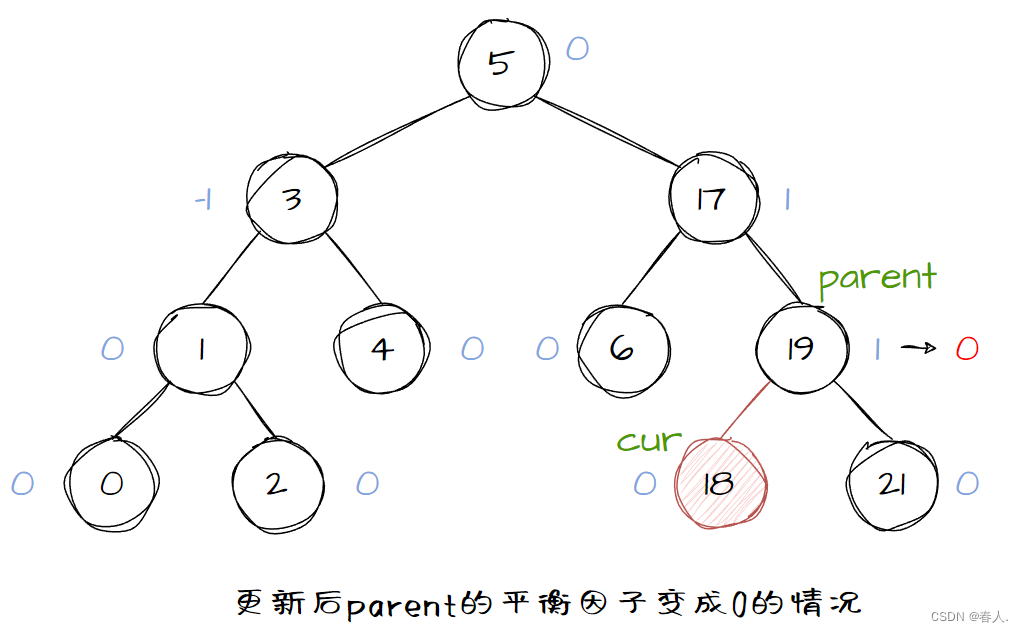
After a new node is inserted, the balance of the AVL tree may be destroyed. At this time, it is necessary to update the balance factor and detect whether the balance of the AVL tree is destroyed. Assuming that the newly inserted node is cur, then curthe balance factor of must be 0, because all its left-back children are nullptr. However cur, the balance factor of the parent node parentmust be adjusted. Before insertion, parentthe balance factor of is divided into three situations: -1, 0, and 1. The parentadjustment of the balancing factor is divided into the following two situations:

If curis inserted to parentthe left of , we only need to give parentthe balancing factor of $- 1$ is enough.
If curis inserted to parentthe right of , just give parentthe balancing factor of $+ 1$ is enough.

At this time, the updated parentbalance factor has the following three situations: $0$ 、 $\pm 1$ 、 $\pm 2$

If parentthe balance factor of is $0$ , indicating thatparentthe balance factor before insertion must be $\pm 1$ , that is, one of the left and right children must benullptr, and the new node is inserted on the empty side. After the insertion, the balance factor is adjusted to $0$ , the height of the entire tree remains unchanged, satisfying the properties of the AVL tree, and the insertion is successful.
If parentthe balance factor of is $\pm 1$ , indicating thatparentthe balance factor before insertion must be $0$ , that is, the left and right children of before insertionparentare allnullptr, and no new node is inserted onparenteither side of , so the balance factor is adjusted to $\pm 1.$ At this time, it is considered parentthat $0$ , the update ends at this time and the insertion is successful.
If parentthe balance factor of is $\pm 2$ , thenparentthe balance factor of violates the properties of the balanced tree and needs to be rotated.

Situation one:
Insert image description here
Situation two:

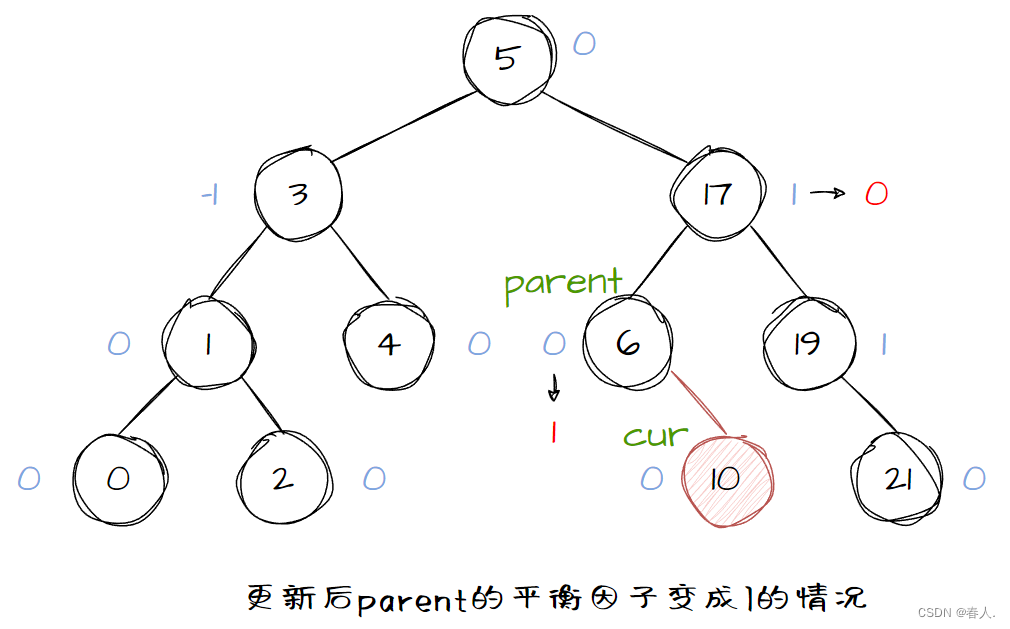
Situation three:

5.2 Rotation of AVL tree

If a new node is inserted into an originally balanced AVL tree, it may cause imbalance. At this time, the structure of the tree must be adjusted to make it balanced. Depending on the insertion position of the node, the rotation of the AVL tree is divided into four types:

5.2.1 Single left rotation

The new node is inserted on the right side of the higher right subtree - right right: that is, parentthe balance factor of is $2$ ,curthe balancing factor is $1$ , then left single rotation is required. Here are two examples of left-handed rotation.

Example 1:
Insert image description here
Example 2:

Abstract diagram:

Tips : No matter which one of these four rotations is used, the following two points must be ensured: firstly, during the rotation process, the tree must be a search tree, and secondly, after rotation, the tree should become a balanced tree. And reduce the height of this subtree. These two points determine that the core operation of left rotation is to curgive the left subtree of to parentthe right subtree of , and then let parentbecome curthe left subtree of .

void RotateL(Node* parent)
{
    
    
	Node* cur = parent->_right;
	Node* curleft = cur->_left;

	parent->_right = curleft;
	cur->_left = parent;

	if (curleft)
	{
    
    
		curleft->_parent = parent;
	}
	
	Node* ppnode = parent->_parent;
	parent->_parent = cur;

	if (parent == _root)
	{
    
    
		_root = cur;
		cur->_parent = nullptr;
	}
	else
	{
    
    
		if (ppnode->_left == parent)
		{
    
    
			ppnode->_left = cur;
		}
		else
		{
    
    
			ppnode->_right = cur;
		}
		cur->_parent = ppnode;
	}
	parent->_bf = cur->_bf = 0;
}

5.2.2 Right-hand single rotation

The new node is inserted on the left side of the higher left subtree----leftleft: that is, parentthe balance factor of is $- 2$ ,curthe equilibrium factor is $- 1$ , then a right single rotation is required.

Abstract diagram:
Insert image description here

//右单旋
void RotateR(Node* parent)
{
    
    
	Node* cur = parent->_left;
	Node* curright = cur->_right;//此时的情况是curright比cur大，比parent小

	parent->_left = curright;
	cur->_right = parent;

	if (curright)
	{
    
    
		curright->_parent = parent;
	}
	
	Node* ppnode = parent->_parent;
	parent->_parent = cur;

	if (ppnode)
	{
    
    
		cur->_parent = ppnode;
		if (ppnode->_left == parent)
		{
    
    
			ppnode->_left = cur;
		}
		else
		{
    
    
			ppnode->_right = cur;
		}
	}
	else
	{
    
    
		_root = cur;
		cur->_parent = nullptr;
	}
	parent->_bf = cur->_bf = 0;
}

5.2.3 First turn right and then turn left

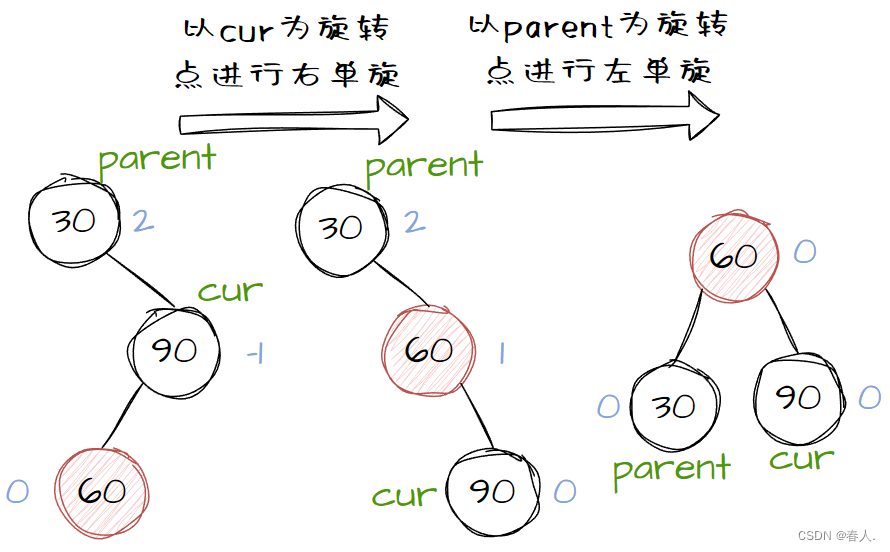
The new node is inserted to the left of the higher right subtree----right and left: that is, parentthe balance factor of is $2$ ,curthe equilibrium factor is $-1$ . $_$ At this time, you need to first perform a right single rotation using curasparentperform a left single rotation using as the rotation point. Here are two examples for you.

Example 1:
Insert image description here
Example 2:

Abstract diagram:

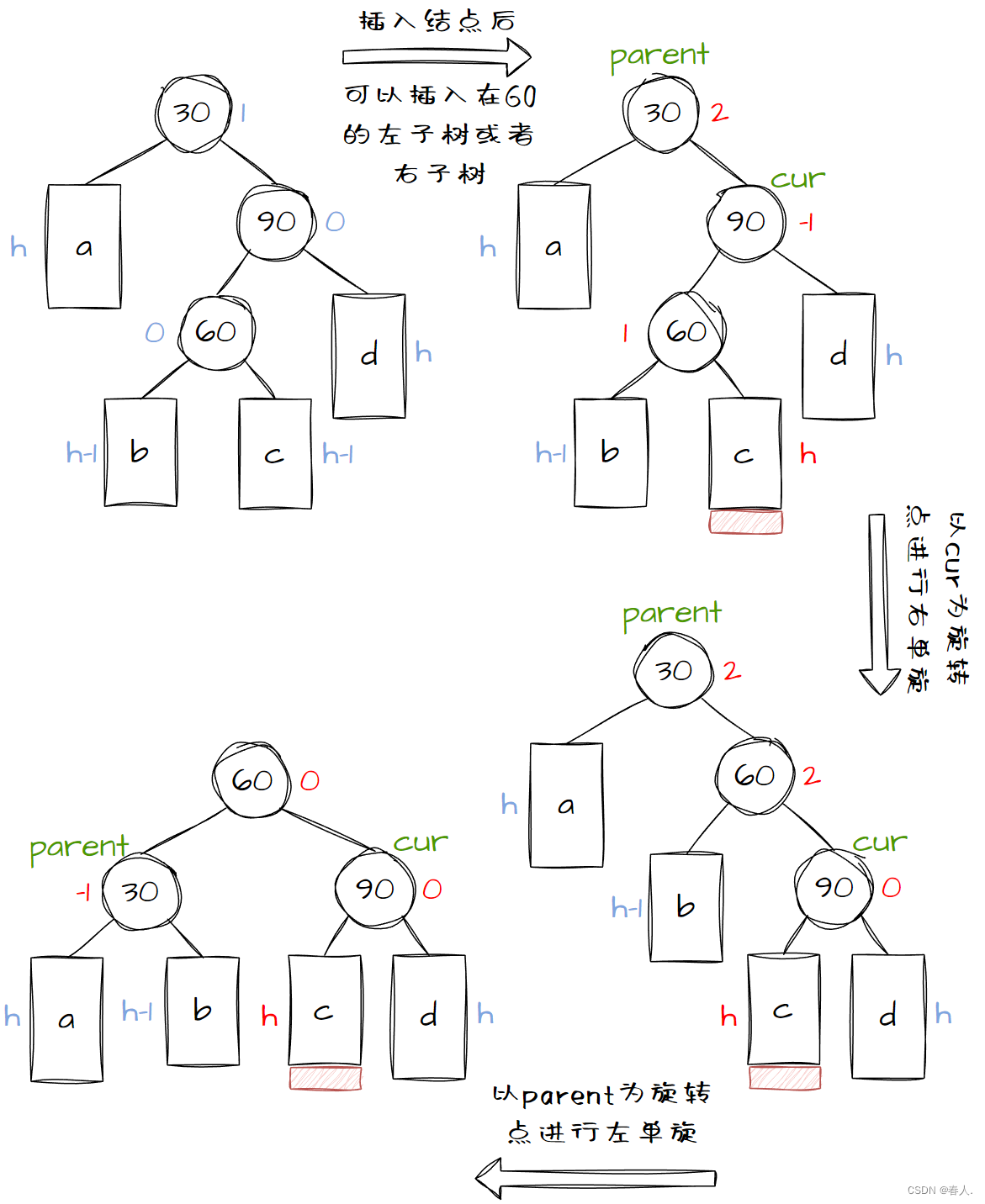
Tips : The essence of the right-left double rotation is to give the right side of the 60 node to the left side of the 90 node, and give the left side of the 60 node to the right side of the 30 node, and then the 60 node Becomes the node of this subtree. After right and left double rotation, the balance factor will be updated in the following three situations:

The balance factor of 60 nodes after insertion is $0$ , indicating that 60 itself is a new node. At this time,the balance factors ofparentandcur $0$ 。
The balance factor of 60 nodes after insertion is $- 1$ , indicating that it is inserted on the left side of node 60. At this time,parentthe balance factor is $0$ ,curthe equilibrium factor is $- 1$ 。
The balance factor of 60 nodes after insertion is $1$ , indicating that it is inserted on the right side of node 60. At this time,parentthe balance factor is $- 1$ ,curthe equilibrium factor is $0$ 。

//右左双旋
void RotateRL(Node* parent)
{
    
    
	Node* cur = parent->_right;
	Node* curleft = cur->_left;
	int bf = curleft->_bf;

	RotateR(parent->_right);
	RotateL(parent);

	if (bf == 0)
	{
    
    
		parent->_bf = cur->_bf = curleft->_bf = 0;
	}
	else if (bf == 1)
	{
    
    
		cur->_bf = 0;
		parent->_bf = -1;
		curleft->_bf = 0;
	}
	else if (bf == -1)
	{
    
    
		cur->_bf = 1;
		parent->_bf = 0;
		curleft->_bf = 0;
	}
}

5.2.4 First turn left and then turn right

The new node is inserted on the right side of the higher left subtree----left and right: that is, parentthe balance factor of is $- 2$ ,curthe equilibrium factor is $1$ . At this time, you need to first perform a left single rotation using curasparentperform a right single rotation using as the rotation point. Here are two specific examples for you.

Example 1:
Insert image description here
Example 2:

Abstract diagram:

5.3 Insert complete code into AVL tree

/*AVLTree.h*/
public:
	bool Insert(const pair<K, V>& kv)
	{
    
    
		if (_root == nullptr)
		{
    
    
			_root = new Node(kv);
			return true;//插入成功
		}
	
		//找插入位置
		Node* cur = _root;
		Node* parent = nullptr;
	
		while (cur)
		{
    
    
			if (kv.first < cur->_kv.first)//小于往左走
			{
    
    
				parent = cur;
				cur = cur->_left;
			}
			else if (kv.first > cur->_kv.first)//大于往右走
			{
    
    
				parent = cur;
				cur = cur->_right;
			}
			else//相等插入不了
			{
    
    
				return false;
			}
		}
	
		//找到待插入位置了，进行插入
		cur = new Node(kv);
		if (kv.first < parent->_kv.first)
		{
    
    
			parent->_left = cur;
		}
		else
		{
    
    
			parent->_right = cur;
		}
	
		cur->_parent = parent;
	
		//控制平衡
		//更新衡因子
		while (parent)//我们这里始终更新的是parent的平衡银子，当parent为nullptr说明根节点_root的平衡因子已经被我们更新过了
		{
    
    
			//更新平衡因子
			if (cur == parent->_left)
			{
    
    
				--(parent->_bf);
			}
			else if (cur == parent->_right)
			{
    
    
				++(parent->_bf);
			}
	
			//判断更新后parent的平衡因子
			if (parent->_bf == 0)//输入成功
			{
    
    
				break;
			}
			else if (parent->_bf == -1 || parent->_bf == 1)
			{
    
    
				//继续往上更新
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == -2 || parent->_bf == 2)
			{
    
    
				//需要旋转
				if (cur->_bf == 1 && parent->_bf == 2)//左单旋
				{
    
    
					RotateL(parent);
				}
				else if (cur->_bf == -1 && parent->_bf == -2)//右单旋
				{
    
    
					RotateR(parent);
				}
				else if (cur->_bf == -1 && parent->_bf == 2)//右左单旋
				{
    
    
					RotateRL(parent);
				}
				else if (cur->_bf == 1 && parent->_bf == -2)//左右单旋
				{
    
    
					RotateLR(parent);
				}
	
				break;
			}
			else
			{
    
    
				assert(false);
			}
		}
	
		return true;
	}
	
	
private:
	//左单旋
	void RotateL(Node* parent)
	{
    
    
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
	
		parent->_right = curleft;
		cur->_left = parent;
	
		if (curleft)
		{
    
    
			curleft->_parent = parent;
		}
		
		Node* ppnode = parent->_parent;
		parent->_parent = cur;
	
		if (parent == _root)
		{
    
    
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
    
    
			if (ppnode->_left == parent)
			{
    
    
				ppnode->_left = cur;
			}
			else
			{
    
    
				ppnode->_right = cur;
			}
			cur->_parent = ppnode;
		}
	
		parent->_bf = cur->_bf = 0;
	}
	
	//右单旋
	void RotateR(Node* parent)
	{
    
    
		Node* cur = parent->_left;
		Node* curright = cur->_right;//此时的情况是curright比cur大，比parent小
	
		parent->_left = curright;
		cur->_right = parent;
	
		if (curright)
		{
    
    
			curright->_parent = parent;
		}
		
		Node* ppnode = parent->_parent;
		parent->_parent = cur;
	
		if (ppnode)
		{
    
    
			cur->_parent = ppnode;
			if (ppnode->_left == parent)
			{
    
    
				ppnode->_left = cur;
			}
			else
			{
    
    
				ppnode->_right = cur;
			}
		}
		else
		{
    
    
			_root = cur;
			cur->_parent = nullptr;
		}
		parent->_bf = cur->_bf = 0;
	}
	
	//右左双旋
	void RotateRL(Node* parent)
	{
    
    
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		int bf = curleft->_bf;
	
		RotateR(parent->_right);
		RotateL(parent);
	
		if (bf == 0)
		{
    
    
			parent->_bf = cur->_bf = curleft->_bf = 0;
		}
		else if (bf == 1)
		{
    
    
			cur->_bf = 0;
			parent->_bf = -1;
			curleft->_bf = 0;
		}
		else if (bf == -1)
		{
    
    
			cur->_bf = 1;
			parent->_bf = 0;
			curleft->_bf = 0;
		}
	}
	
	//左右双旋
	void RotateLR(Node* parent)
	{
    
    
		Node* cur = parent->_left;
		Node* curright = cur->_right;
		int bf = curright->_bf;
	
		RotateL(cur);
		RotateR(parent);
	
		if (bf == 0)
		{
    
    
			parent->_bf = cur->_bf = curright->_bf = 0;
		}
		else if (bf == 1)
		{
    
    
			parent->_bf = 0;
			cur->_bf = -1;
			curright->_bf = 0;
		}
		else if (bf == -1)
		{
    
    
			parent->_bf = 1;
			cur->_bf = 0;
			curright->_bf = 0;
		}
	}

5.4 Verification of AVL trees

The AVL tree adds balanced restrictions on the basis of the binary search tree. Therefore, to verify the AVL tree, it can be divided into two steps:

Verify that it is a binary search tree. If an in-order traversal can obtain an ordered sequence, it is a binary search tree.
Verify that it is a balanced tree. The absolute value of the height difference between the left and right subtrees of each node does not exceed $1$ . Secondly, check whether the balance factor of the node is calculated correctly.

public:
	//中序
	void Inorder()
	{
    
    
		return _Inorder(_root);
	}
	//检测平衡因子
	bool IsBlance()
	{
    
    
		return _IsBalance(_root);
	}
private:
	//中序
	void _Inorder(Node* root)
	{
    
    
		if (root == nullptr)
		{
    
    
			return;
		}
	
		_Inorder(root->_left);
		cout << root->_kv.first << ' ';
		_Inorder(root->_right);
	
		return;
	}
	
	
	//求树的高度
	int Height(Node* root)
	{
    
    
		if (root == nullptr)
		{
    
    
			return 0;
		}

		int leftHeight = Height(root->_left);
		int rightHeight = Height(root->_right);

		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}
	
	//检测平衡因子
	bool _IsBalance(Node* root)
	{
    
    
		if (root == nullptr)
		{
    
    
			return true;
		}

		int leftHeight = Height(root->_left);
		int rightHeight = Height(root->_right);

		if (rightHeight - leftHeight != root->_bf)
		{
    
    
			cout << "平衡因子异常:" << root->_bf << endl;
			return false;
		}

		return abs(leftHeight - rightHeight) < 2
			&& _IsBalance(root->_left)
			&& _IsBalance(root->_right);
	}

/*test.c*/
int main()
{
    
    
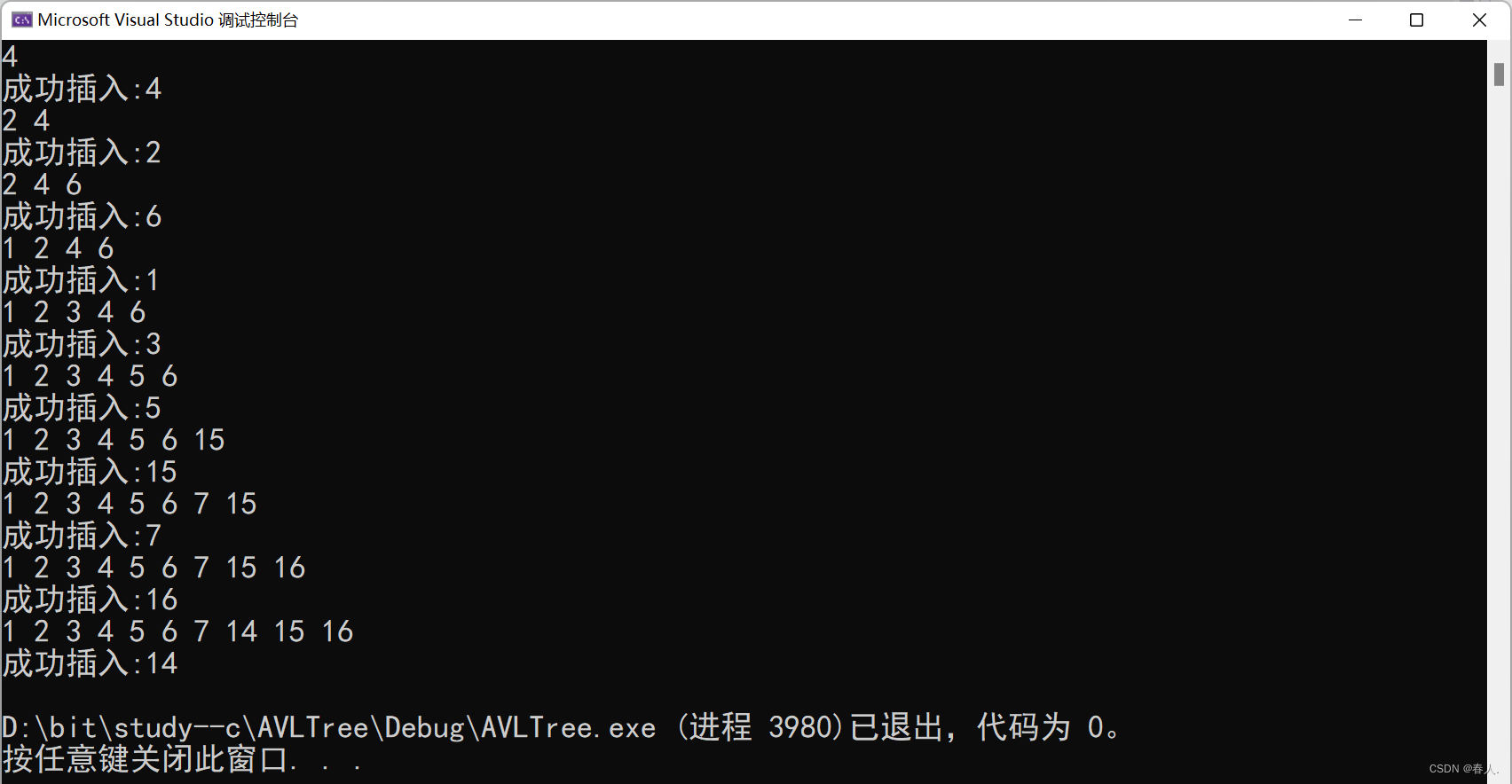
	int a[] = {
    
     4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	wcy::AVLTree<int, int> t;
	for (auto e : a)
	{
    
    
		t.Insert(make_pair(e, e));
		t.Inorder();
		cout << endl;
		if (t.IsBlance())
		{
    
    
			cout << "成功插入:" << e << endl;
		}
		else
		{
    
    
			cout << e << "插入失败" << endl;
		}
	}
	return 0;
}

Insert image description here

6. Deletion of AVL tree

Because the AVL tree is also a binary search tree, the node can be deleted according to the binary search tree method, and then the balance factor is updated. However, unlike deletion and insertion, the balance factor is updated after the node is deleted. In the worst case Always adjust to the position of the root node. Friends who are interested in specific implementation can refer to "Introduction to Algorithms" or "Data Structure - Description Using Object-Oriented Methods and C++" Yin Renkun Edition.

7. Performance of AVL tree

The AVL tree is an absolutely balanced binary search tree, which requires that the absolute value of the height difference between the left and right subtrees of each node does not exceed $1$ , which can ensure efficient time complexity when querying, that is, $O(log2^n)$ . However, if you want to make some structural modifications to the AVL tree, the performance is very low. For example, when inserting, you need to maintain its absolute balance, and the number of rotations is relatively high. What's worse is that when deleting, it is possible to continue the rotation until the root. s position. Therefore, if you need a data structure with efficient query and ordering, and the number of data is static (that is, it will not change), you can consider the AVL tree. However, if a structure is frequently modified, it is not suitable.

8. Conclusion

Today’s sharing ends here! If you think the article is good, you can support it three times . There are many interesting articles on Chunren's homepage . Friends are welcome to comment. Your support is the driving force for Chunren to move forward!

Insert image description here