Time Series Analysis - Based on R | Chapter 3 Properties of ARMA Model
Previous articles
Time series analysis - based on R | Chapter 1 exercise code
Time series analysis - based on R | Chapter 2 preprocessing exercise code of time series
-
It is known that a certain AR (1) AR(1)A R ( 1 ) model is:xt = 0.7 xt − 1 + ε t , ε t ∼ WN ( 0 , 1 ). x_t=0.7x_{t-1}+\varepsilon_t,\varepsilon_t \sim WN(0,1).xt=0.7x _t−1+et,et∼WN(0,1).求 E ( x t ) , V a r ( x t ) , ρ 2 E(x_t),Var(x_t),\rho_2 And ( xt),There is ( xt),r2and ϕ 22 . \phi_{22}.ϕ22.
E ( x t ) = ϕ 0 1 − ϕ 1 = 0 1 − 0.7 = 0 E\left(x_t\right)=\frac{\phi_{0}}{1-\phi_{1}}=\frac{0}{1-0.7}=0 E(xt)=1 − ϕ1ϕ0=1−0.70=0
V a r ( x t ) = 1 1 − ϕ 1 2 = 1 1 − 0. 7 2 = 1.96 Var(x_t)=\frac{1}{1-\phi_{1}^{2}}=\frac{1}{1-0.7^2}=1.96 There is ( xt)=1 − ϕ121=1−0.721=1.96
ρ 2 = ϕ 1 2 = 0.7 2 = 0.49 \rho_2=\phi_1^2=0.7^2=0.49r2=ϕ12=0.72=0.49
ϕ 22 = ∣ 1 ρ 1 ρ 1 ρ 2 ∣ ∣ 1 ρ 1 ρ 1 1 ∣ = 0.49 − 0. 7 2 1 − 0. 7 2 = 0 \phi_{22}=\frac{\left|\begin{array}{cc}1 & \rho_{1} \\\rho_{1} & \rho_{2}\end{array}\right|}{\left|\begin{array}{cc}1 & \rho_{1} \\\rho_{1} & 1\end{array}\right|}=\frac{0.49-0.7^{2}}{1-0.7^{2}}=0 ϕ22= 1r1r11 1r1r1r2 =1−0.720.49−0.72=0
-
It is known that a certain AR ( 2 ) \operatorname{AR}(2)AR ( 2 ) model:xt = ϕ 1 xt − 1 + ϕ 2 xt − 2 + ε t , ε t ∼ WN ( 0 , σ ε 2 ) x_t=\phi_1 x_{t-1}+\phi_2 x_{ t-2}+\varepsilon_t, \varepsilon_t \sim WN\left(0, \sigma_{\varepsilon}^2\right)xt=ϕ1xt−1+ϕ2xt−2+et,et∼WN(0,pe2) , andρ 1 = \rho_1=r1= 0.5 , ρ 2 = 0.3 0.5, \rho_2=0.3 0.5,r2=0.3 , 求ϕ 1 , ϕ 2 \phi_1, \phi_2ϕ1,ϕ2value.
A R ( 2 ) A R(2) A R ( 2 ) model:
{ ρ 1 = ϕ 1 1 − ϕ 2 ρ 2 = ϕ 1 ρ 1 + ϕ 2 ⇒ { 0.5 = ϕ 1 1 − ϕ 2 0.3 = 0.5 ϕ 1 + ϕ 2 ⇒ { ϕ 1 = 7 15 , ϕ 2 = 1 15 ϕ 2 = 1 15 \left\{\begin{array} { l } { \rho _ { 1 } = \frac { \phi _ { 1 } } { 1 - \phi _ { 2 } } } \\ { \rho _ { 2 } = \phi _ { 1 } \rho _ { 1 } + \phi _ { 2 } } \end{array} \Rightarrow \left\{\begin{array } { l } { 0 . 5 = \frac { \phi _ { 1 } } { 1 - \phi _ { 2 } } } \\ { 0 . 3 = 0. 5 \phi _ { 1 } + \phi _ { 2 } } \end{array} \Rightarrow \left\{\begin{array}{l} \phi_1=\frac{7}{15}, \phi_2=\ frac{1}{15} \\ \phi_2=\frac{1}{15} \end{array}\right.\right.\right.{ r1=1 − ϕ2ϕ1r2=ϕ1r1+ϕ2⇒{ 0.5=1 − ϕ2ϕ10.3=0.5 ϕ1+ϕ2⇒{ ϕ1=157,ϕ2=151ϕ2=151 -
It is known that a certain AR ( 2 ) \operatorname{AR}(2)The AR ( 2 ) model is:(1 − 0.5 B) (1 − 0.3 B) xt = ε t, ε t ∼ WN (0, 1) (1-0.5 B)(1-0.3 B) x_t=\varepsilon_t, \varepsilon_t \sim WN(0,1)(1−0.5B)(1−0.3 B ) xt=et,et∼WN(0,1), 求 E ( x t ) E\left(x_t\right) E(xt) ,Var ( xt ) , ρ k , ϕ kk \operatorname{Var}\left(x_t\right), \rho_k, \phi_{kk}Was(xt),rk,ϕkk, where k = 1, 2, 3 k=1,2,3k=1,2,3.
(1) ( 1 − 0.5 B ) ( 1 − 0.3 B ) x t = ε t ⇔ x t = 0.8 x t − 1 − 0.15 x t − 2 + ε t (1-0.5 B)(1-0.3 B) x_t=\varepsilon_t \Leftrightarrow x_t=0.8 x_{t-1}-0.15 x_{t-2}+\varepsilon_t (1−0.5B)(1−0.3 B ) xt=et⇔xt=0.8 xt−1−0.15xt−2+et
E ( xt ) = ϕ 0 1 − ϕ 1 − ϕ 2 = 0 E\left(x_t\right)=\frac{\phi_0}{1-\phi_1-\phi_2}=0E(xt)=1−ϕ1−ϕ2ϕ0=0
(2)
Var ( x t ) = 1 − ϕ 2 ( 1 + ϕ 2 ) ( 1 − ϕ 1 − ϕ 2 ) ( 1 + ϕ 1 − ϕ 2 ) = 1 + 0.15 ( 1 − 0.15 ) ( 1 − 0.8 + 0.15 ) ( 1 + 0.8 + 0.15 ) = 1.98 \begin{aligned} \operatorname{Var}\left(x_t\right) & =\frac{1-\phi_2}{\left(1+\phi_2\right)\left(1-\phi_1-\phi_2\right)\left(1+\phi_1-\phi_2\right)} \\ & =\frac{1+0.15}{(1-0.15)(1-0.8+0.15)(1+0.8+0.15)} \\ & =1.98 \end{aligned} Was(xt)=(1+ϕ2)(1−ϕ1−ϕ2)(1+ϕ1−ϕ2)1−ϕ2=(1−0.15)(1−0.8+0.15)(1+0.8+0.15)1+0.15=1.98
(3)
ρ 1 = ϕ 1 1 − ϕ 2 = 0.8 1 + 0.15 = 0.70 ρ 2 = ϕ 1 ρ 1 + ϕ 2 = 0.8 × 0.7 − 0.15 = 0.41 ρ 3 = ϕ 1 ρ 2 + ϕ 2 ρ 1 = 0.8 × 0.41 − 0.15 × 0.7 = 0.22 \begin{aligned} & \rho_1=\frac{\phi_1}{1-\phi_2}=\frac{0.8}{1+0.15}=0.70 \\ & \rho_2=\ phi_1 \rho_1+\phi_2=0.8 \times 0.7-0.15=0.41 \\ & \rho_3=\phi_1 \rho_2+\phi_2 \rho_1=0.8 \times 0.41-0.15 \times 0.7=0.22 \end{aligned}r1=1−ϕ2ϕ1=1+0.150.8=0.70r2=ϕ1r1+ϕ2=0.8×0.7−0.15=0.41r3=ϕ1r2+ϕ2r1=0.8×0.41−0.15×0.7=0.22
(4)
ϕ 11 = ρ 1 = 0.7 ϕ 22 = ϕ 2 = − 0.15 ϕ 33 = 0 \begin{aligned} \phi_{11} & =\rho_1=0.7 \\ \phi_{22} & =\phi_2= -0.15 \\ \phi_{33} & =0 \end{aligned}ϕ11ϕ22ϕ33=r1=0.7=ϕ2=−0.15=0 -
It is known that AR ( 2 ) \operatorname{AR}(2)The sequence of AR ( 2 ) is xt = xt − 1 + cxt − 2 + ε t x_t=x_{t-1}+c x_{t-2}+\varepsilon_txt=xt−1+cxt−2+et, where { ε t } \left\{\varepsilon_t\right\}{ et} is a white noise sequence. DetermineccThe value range of c is to ensure that{ xt } \left\{x_t\right\}{ xt} is a stationary sequence, and the sequenceρ k \rho_krkexpression.
(1) A R ( 2 ) A R(2) The stationary condition of the A R ( 2 ) model is
{ ∣ c ∣ < 1 c ± 1 < 1 ⇒ { − 1 < c < 1 c < 0 ⇒ − 1 < c < 0 \left\{\begin{array}{l}|c|<1 \\ c \pm 1<1\end{array} \Rightarrow\left\{\begin{array}{l}-1<c<1 \\ c<0\end{array} \Rightarrow-1<c<0\right.\right. { ∣c∣<1c±1<1⇒{ −1<c<1c<0⇒−1<c<0
(2) { ρ 1 = 1 1 − c , ρ k = ρ k − 1 + c ρ k − 2 , k ≥ 2 \left\{\begin{array}{l}\rho_{1}=\frac{ 1}{1-c}, \\\rho_{k}=\rho_{k-1}+c \rho_{k-2}, k \geq 2\end{array}\right.{ r1=1−c1,rk=rk−1+cρk−2,k≥2
-
Prove that for any constant ccc , AR (3) defined as follows\mathrm{AR}(3)The AR ( 3 ) sequence must be a non-stationary sequence:
xt = xt − 1 + cxt − 2 − cxt − 3 + ε t , ε t ∼ WN ( 0 , σ ε 2 ) x_t=x_{t-1}+c x_{ t-2}-c x_{t-3}+\varepsilon_t, \varepsilon_t \sim WN\left(0, \sigma_{\varepsilon}^2\right)xt=xt−1+cxt−2−cxt−3+et,et∼WN(0,pe2)
Proof:
The characteristic equation of this sequence is: λ 3 − λ 2 − c λ + c = 0 \lambda^{3}-\lambda^{2}-c \lambda+c=0l3−l2−c l+c=0 , solving this characteristic equation yields three characteristic roots:
λ 1 = 1 , λ 2 = c , λ 3 = − c \lambda_{1}=1, \quad \lambda_{2}=\sqrt{c}, \quad \lambda_{3}=-\sqrt{c} l1=1,l2=c,l3=−c
Regardless of ccNo matter what value c takes, this equation has a characteristic root on the unit circle, so the sequence must be a non-stationary sequence. Certification completed.
-
For AR ( 1 ) \mathrm{AR}(1)AR ( 1 ) model:xt = ϕ 1 xt − 1 + ε t , ε t ∼ WN ( 0 , σ ε 2 ) x_t=\phi_1 x_{t-1}+\varepsilon_t, \varepsilon_t \sim WN\left( 0, \sigma_{\varepsilon}^2\right)xt=ϕ1xt−1+et,et∼WN(0,pe2) , determine whether the following proposition is correct:
(1)γ 0 = ( 1 + ϕ 1 2 ) σ ε 2 \gamma_0=\left(1+\phi_1^2\right) \sigma_{\varepsilon}^2c0=(1+ϕ12)pe2
(2) E [ ( x t − μ ) ( x t − 1 − μ ) ] = − ϕ 1 E\left[\left(x_t-\mu\right)\left(x_{t-1}-\mu\right)\right]=-\phi_1 E[(xt−m )(xt−1−m ) ]=− ϕ1
(3) ρ k = ϕ 1 k \rho_k=\phi_1^krk=ϕ1k
(4) ϕ kk = ϕ 1 k \phi_{kk}=\phi_1^kϕkk=ϕ1k
(5) ρ k = ϕ 1 ρ k − 1 \rho_k=\phi_1\rho_{k-1}rk=ϕ1rk−1
Sure! Here are the answers and calculation processes for each statement:
(1) 错误。 γ 0 = σ ε 2 1 − ϕ 1 2 \gamma_0=\frac{\sigma_{\varepsilon}^2}{1-\phi_1^2} c0=1 − ϕ12pe2。
(2) 错误。 E [ ( x t − μ ) ( x t − 1 − μ ) ] = ϕ 1 γ 1 E\left[ \left(x_t-\mu\right)\left(x_{t-1}-\mu\right) \right]=\phi_1\gamma_1 E[(xt−m )(xt−1−m ) ]=ϕ1c1Let
E ( xt ) = E [ ϕ 1 xt − 1 + ε t ] = ϕ 1 E ( xt − 1 ) + E ( ε t ) = ϕ 1 E ( xt ) + 0 = 0 \begin{aligned } E(x_t) &= E[\phi_1x_{t-1}+\varepsilon_t] \\ &= \phi_1E(x_{t-1})+E(\varepsilon_t) \\ &= \phi_1E(x_t)+ 0 \\ &= 0 \end{aligned}And ( xt)=E [ ϕ1xt−1+et]=ϕ1And ( xt−1)+E ( et)=ϕ1And ( xt)+0=0
From this we can get μ = 0 \mu=0m=0も,Given:
E [ ( xt − μ ) ( xt − 1 − μ ) ] = E [ xtxt − 1 ] = E [ ( ϕ 1 xt − 1 + ε t ) xt − 1 ] = ϕ 1 E xt − 1 2 ] + E [ ε txt − 1 ] = ϕ 1 γ 0 \begin{aligned} E\left[\left(x_t-\mu\right)\left(x_{t-1}-\mu\ right)\right] &= E[x_tx_{t-1}] \\ &= E[(\phi_1x_{t-1}+\varepsilon_t)x_{t-1}] \\ &= \phi_1 E[x_ {t-1}^2] + E[\varepsilon_t x_{t-1}] \\ &= \phi_1 \gamma_0 \end{aligned}E[(xt−m )(xt−1−m ) ]=And [ xtxt−1]=E [( ϕ1xt−1+et)xt−1]=ϕ1And [ xt−12]+E [ etxt−1]=ϕ1c0
Therefore, the proposition is false.
(3) Correct. Since the AR(1) model has stationarity and finite second-order moment properties, when k > 0 k > 0k>When 0 , there isρ k = ϕ 1 k \rho_k=\phi_1^krk=ϕ1k
(4) Definition ϕ kk = { ϕ 1 , k = 1 0 , k ⩾ 2 \phi_{kk}=\begin{cases}\phi_1,&k=1\\ 0,&k\geqslant2\end{cases }ϕkk={ ϕ1,0,k=1k⩾2
(5) Correct. Since the AR(1) model has stationarity and finite second-order moment properties, when k > 0 k > 0k>When 0 , there isρ k = ϕ 1 ρ k − 1 \rho_k=\phi_1\rho_{k-1}rk=ϕ1rk−1。 -
It is known that a certain centralized MA (1) \mathrm{MA}(1)MA ( 1 ) model first-order autocorrelation coefficientρ 1 = 0.4 \rho_1=0.4r1=0.4 , find the expression of this model.
ρ 1 = − θ 1 1 + θ 1 2 = 0.4 ⇒ 0.4 θ 1 2 + θ 1 + 0.4 = 0 ⇒ θ 1 = − 2 or θ 1 = − 1 2 \rho_{ 1}=\frac{-\theta_{1}}{1+\theta_{1}^{2}}=0.4 \Rightarrow 0.4 \theta_{1}^{2}+\theta_{1}+0.4=0 \Rightarrow \theta_{1}=-2 \text { or} \theta_{1}=-\frac{1}{2}r1=1+i12− i1=0.4⇒0.4 i12+i1+0.4=0⇒i1=− 2 or θ 1=−21So the model has two possible expressions: xt = ε t + 1 2 ε t − 1 x_{t}=\varepsilon_{t}+\frac{1}{2} \varepsilon_{t-1}xt=et+21et−1和xt = ε t + 2 ε t − 1 x_{t}=\varepsilon_{t}+2 \varepsilon_{t-1}xt=et+2 et−1 。
-
Determine the constant CCThe value of C is to ensure that the following expression isMA (2) \mathrm{MA}(2)MA ( 2 ) model:
xt = 10 + 0.5 xt − 1 + ε t − 0.8 ε t − 2 + C ε t − 3 x_t=10+0.5 x_{t-1}+\varepsilon_t-0.8 \varepsilon_{t-2}+C \varepsilon_ {t-3}xt=10+0.5x _t−1+et−0.8 et−2+C εt−3
将xt = 10 + 0.5 xt − 1 + ε t − 0.8 ε t − 2 + C ε t − 3 x_{t}=10+0.5 x_{t-1}+\varepsilon_{t}-0.8 \varepsilon_{ t-2}+C \varepsilon_{t-3}xt=10+0.5x _t−1+et−0.8 et−2+C εt−3The equivalent expression is
xt − 10 = 1 − 0.8 B 2 + c B 3 1 − 0.5 B ε t = ( 1 + a B + b B 2 ) ε t x_{t}-10=\frac{1-0.8 B ^{2}+c B^{3}}{1-0.5 B} \varepsilon_{t}=\left(1+a B+b B^{2}\right) \varepsilon_{t}xt−10=1−0.5B1−0.8B2+cB3et=(1+aB+bB2)et
Rules
1 − 0.8 B 2 + c B 3 = ( 1 + a B + b B 2 ) ( 1 − 0.5 B ) = 1 + ( a − 0.5 ) B + ( b − 0.5 a ) B 2 − 0.5 b B 3 \begin{aligned} 1-0.8 B^{2}+c B^{3} & =\left(1+a B+b B^{2}\right)(1-0.5 B) \\ & =1+(a-0.5) B+(b-0.5 a) B^{2}-0.5 b B^{3} \end{aligned} 1−0.8B2+cB3=(1+aB+bB2)(1−0.5B)=1+(a−0.5)B+(b−0.5a)B2−0.5 bB _3
According to the undetermined coefficient method:
− 0.8 = a − 0.5 ⇒ a = − 0.3 0 = − 0.5 b ⇒ b = 0 c = b − 0.5 a ⇒ c = 0.15 \begin{aligned} -0.8 & =a-0.5 \Rightarrow a=-0.3 \\ 0 & =-0.5 b \Rightarrow b=0 \\ c & =b-0.5 a \Rightarrow c=0.15 \end{aligned} −0.80c=a−0.5⇒a=−0.3=−0.5b⇒b=0=b−0.5 a⇒c=0.15
-
Known MA (2) \mathrm{MA}(2)MA ( 2 ) model:xt = ε t − 0.7 ε t − 1 + 0.4 ε t − 2 , ε t ∼ WN ( 0 , σ ε 2 ) x_t=\varepsilon_t-0.7 \varepsilon_{t-1}+0.4 \varepsilon_{t-2}, \varepsilon_t \sim WN\left(0, \sigma_{\varepsilon}^2\right)xt=et−0.7εt−1+0.4εt−2,εt∼WN(0,σε2). 求 E ( x t ) , Var ( x t ) E\left(x_t\right), \operatorname{Var}\left(x_t\right) E(xt),Var(xt), 及 ρ k ( k ⩾ 1 ) \rho_k(k \geqslant 1) ρk(k⩾1).
(1) E ( x t ) = 0 E\left(x_{t}\right)=0 E(xt)=0
(2) Var ( x t ) = 1 + 0. 7 2 + 0. 4 2 = 1.65 \operatorname{Var}\left(x_{t}\right)=1+0.7^{2}+0.4^{2}=1.65 Var(xt)=1+0.72+0.42=1.65
(3) ρ 1 = − 0.7 − 0.7 × 0.4 1.65 = − 0.59 , ρ 2 = 0.4 1.65 = 0.24 , ρ k = 0 , k ≥ 3 \rho_{1}=\frac{-0.7-0.7 \times 0.4} {1.65}=-0.59, \quad \rho_{2}=\frac{0.4}{1.65}=0.24, \quad \rho_{k}=0, k \geq 3r1=1.65−0.7−0.7×0.4=−0.59,r2=1.650.4=0.24,rk=0,k≥3
-
prove:
(1) For any constant ccc , the infinite-order MA sequence defined as follows must be a non-stationary sequence:
xt = ε t + c ( ε t − 1 + ε t − 2 + ⋯ ) , ε t ∼ WN ( 0 , σ ε 2 ) x_{t}= \varepsilon_{t}+c\left(\varepsilon_{t-1}+\varepsilon_{t-2}+\cdots\right), \quad \varepsilon_{t} \sim WN\left(0, \sigma_{ \varepsilon}^{2}\right)xt=et+c( et−1+et−2+⋯),et∼WN(0,pe2)Proof: Because for any constant C, we have
Var ( xt ) = lim k → ∞ ( 1 + k C 2 ) σ ε 2 = ∞ \operatorname{Var}\left(x_{t}\right)=\lim_{k\rightarrow\infty}\ left ( 1 + k C ^ { 2 } \ right ) \ sigma_ { \ productpsilon } ^ { 2 } = \ inftyWas(xt)=k→∞lim(1+kC2)pe2=∞
Therefore, this series is a non-stationary series.
(2) { x t } \left\{x_{t}\right\} { xtThe first-order difference sequence of } must be a stationary sequence, and find { yt } \left\{y_{t}\right\}{ yt} Autocorrelation coefficient expression:
yt = xt − xt − 1 y_{t}=x_{t}-x_{t-1}yt=xt−xt−1yt = xt − xt − 1 = ε t + ( C − 1 ) ε t − 1 y_{t}=x_{t}-x_{t-1}=\varepsilon_{t}+(C-1) \varepsilon_ {t-1}yt=xt−xt−1=et+(C−1 ) et−1, then the sequence { yt } \left\{y_{t}\right\}{ yt} Satisfy the following conditions:
The mean and variance are constants,
E ( yt ) = 0 , Var ( yt ) = [ 1 + ( C − 1 ) 2 ] σ ε 2 E\left(y_{t}\right)=0, \operatorname{Var}\left(y_{ t}\right)=\left[1+(C-1)^{2}\right] \sigma_{\varepsilon}^{2}E(yt)=0,Was(yt)=[1+(C−1)2]pe2
The autocorrelation coefficient is only related to the length of the time interval and has nothing to do with the starting time
ρ 1 = C − 1 1 + ( C − 1 ) 2 , ρ k = 0 , k ≥ 2 \rho_{1}=\frac{C-1}{1+(C-1)^{2}}, \rho_{k}=0, k \geqr1=1+(C−1)2C−1,rk=0,k≥2
Therefore, the difference sequence is a stationary sequence.
-
Test the stationarity and reversibility of the following model, where { ε t } \left\{\varepsilon_{t}\right\}{ et} is a white noise sequence:
(1)xt = 0.5 xt − 1 + 1.2 xt − 2 + ε t x_{t}=0.5 x_{t-1}+1.2 x_{t-2}+\varepsilon_{t}xt=0.5x _t−1+1.2 xt−2+et
Test stationarity: The characteristic equation of this model is 1 − 0.5 z − 1.2 z 2 = 0 1-0.5z-1.2z^2=01−0.5 z−1.2 z2=0 , the solution is to obtain the characteristic roots asz 1 = 1.0517, z 2 = − 0.4784 z_1=1.0517,\,z_2=-0.4784z1=1.0517,z2=− 0.4784 . Since the modulus of one of the eigenvalues is greater than 1, the model is not stationary.
(2) xt = 1.1 xt − 1 − 0.3 xt − 2 + ε t x_{t}=1.1 x_{t-1}-0.3 x_{t-2}+\varepsilon_{t}xt=1.1xt−1−0.3x _t−2+et
Test stationarity: The characteristic equation of this model is 1 − 1.1 z + 0.3 z 2 = 0 1-1.1z+0.3z^2=01−1.1 z+0.3 z2=0 , the characteristic roots arez 1 = 0.3667, z 2 = 1.3667 z_1=0.3667, z_2=1.3667z1=0.3667,z2=1.3667 . Since∣ z 2 ∣ > 1 |z_2|>1∣z2∣>1 , so the model is not stationary.
(3) xt = ε t − 0.9 ε t − 1 + 0.3 ε t − 2 x_{t}=\varepsilon_{t}-0.9 \varepsilon_{t-1}+0.3 \varepsilon_{t-2}xt=et−0.9 et−1+0.3 et−2
Test stationarity: The characteristic equation of this model is 1 + 0.9 z − 0.3 z 2 = 0 1+0.9z-0.3z^2=01+0.9 z−0.3 z2=0 , the characteristic roots arez 1 = 0.5, z 2 = − 0.6 z_1=0.5,\,z_2=-0.6z1=0.5,z2=− 0.6 . Since the modulus length of all eigenroots is less than 1, the model is stationary. Testing reversibility: this model is consistent with ARMA(2, 2) (2,2)(2,2 ) The model is the same and therefore also reversible.
(4) xt = ε t + 1.3 ε t − 1 − 0.4 ε t − 2 x_{t}=\varepsilon_{t}+1.3 \varepsilon_{t-1}-0.4 \varepsilon_{t-2}xt=et+1.3 et−1−0.4 et−2
Test stationarity: The characteristic equation of this model is 1 − 1.3 z + 0.4 z 2 = 0 1-1.3z+0.4z^2=01−1.3z _+0.4z2=0 , the solution is to obtain the characteristic roots asz 1 = 1.465, z 2 = 0.272 z_1=1.465,\,z_2=0.272z1=1.465,z2=0.272 . The modulus of one of the eigenvalues is greater than 1, so the model is not stationary. Testing reversibility: this model is consistent with ARMA(2, 2) (2,2)(2,2 ) The models are the same and therefore irreversible.
(5) xt = 0.7 xt − 1 + ε t − 0.6 ε t − 1 x_{t}=0.7 x_{t-1}+\varepsilon_{t}-0.6 \varepsilon_{t-1}xt=0.7x _t−1+et−0.6 et−1
Test stationarity: The characteristic equation of this model is 1 − 0.7 z + 0.6 z 2 = 0 1-0.7z+0.6z^2=01−0.7 z+0.6 z2=0 , the characteristic roots arez 1 = 0.5, z 2 = 1 z_1=0.5,\,z_2=1z1=0.5,z2=1 . The modulus length of one of the characteristic roots is equal to 1, so the reversibility needs to be further tested. Testing reversibility: this model is consistent with ARMA( 1 , 1 ) (1,1)(1,1 ) The models are the same and therefore reversible.
(6) xt = − 0.8 xt − 1 + 0.5 xt − 2 + ε t − 1.1 ε t − 1 x_{t}=-0.8 x_{t-1}+0.5 x_{t-2}+\varepsilon_{ t}-1.1 \varepsilon_{t-1}xt=− 0.8 xt−1+0.5x _t−2+et−1.1 et−1
Test stationarity: The characteristic equation of this model is 1 + 0.8 z − 0.5 z 2 − 1.1 z − 1 = 0 1+0.8z-0.5z^2-1.1z^{-1}=01+0.8z _−0.5 z2−1.1 z−1=0,解得分内根的z 1 = 1.0501 , z 2 = 0.9804 ± 0.1083 i , z 3 = 0.9452 ± 0.2306 i , z 4 = 0.7889 ± 0.5491 i , z 5 = − 0.9258 ± 0.3732 i , z 6 = − 0.967 9 ± 0.2607 i , z 7 = − 0.9720 ± 0.2341 i , z 8 = − 0.9880 ± 0.1402 i , z 9 = − 0.9893 ± 0.1303 i , z 10 = − 1.0000 z_1=1.0501,\,z_2=0.9804\pm0.10 83i, \,z_3=0.9452\pm0.2306i,\,z_4=0.7889\pm0.5491i,\,z_5=-0.9258\pm0.3732i,\,z_6=-0.9679\pm0.2607i,\,z_7=-0.9720\pm0 .2341i,\,z_8=-0.9880\pm0.1402i,\,z_9=-0.9893\pm0.1303i,\,z_{10}=-1.0000z1=1.0501,z2=0.9804±0.1083i,z3=0.9452±0.2306i , _z4=0.7889±0.5491i,z5=−0.9258±0.3732i , _z6=−0.9679±0.2607i , _z7=−0.9720±0.2341 i ,z8=−0.9880±0.1402i,z9=−0.9893±0.1303i , _z10=− 1.0000 . One of the characteristic roots has a modulus greater than 1, so the model is not stationary. Test reversibility: Because the characteristic equation of this model contains an inversion operatorz − 1 z^{-1}z− 1 , so the model is not reversible.
To sum up, (1) is not stationary; (2) is not stationary; (3) is stationary and reversible; (4) is not stationary and irreversible; (5) is stationary and reversible; (6) is not Smooth and irreversible. -
It is known that ARMA ( 1 , 1 ) \operatorname{ARMA}(1,1)ARMA(1,1 ) The model is:xt = 0.6 xt − 1 + ε t − 0.3 ε t − 1 x_{t}=0.6 x_{t-1}+\varepsilon_{t}-0.3 \varepsilon_{t-1}xt=0.6x _t−1+et−0.3 et−1, determine the Green function of the model so that the model can be equivalently expressed as infinite MA \mathrm{MA}MA order model form.
The Green function of this model is:
G 0 = 1 G_{0}=1G0=1
G 1 = ϕ 1 G 0 − θ 1 = 0.6 − 0.3 = 0.3 G_{1}=\phi_{1} G_{0}-\theta_{1}=0.6-0.3=0.3G1=ϕ1G0−i1=0.6−0.3=0.3
G k = ϕ 1 G k − 1 = ϕ 1 k − 1 G 1 = 0.3 × 0. 6 k − 1 , k ≥ 2 G_{k}=\phi_{1} G_{k-1}=\phi_{1}^{k-1} G_{1}=0.3 \times 0.6^{k-1}, k \geq 2 Gk=ϕ1Gk−1=ϕ1k−1G1=0.3×0.6k−1,k≥2
So the model can be equivalently expressed as: xt = ε t + ∑ k = 0 ∞ 0.3 × 0. 6 k ε t − k − 1 x_{t}=\varepsilon_{t}+\sum_{k=0}^ {\infty} 0.3 \times 0.6^{k} \varepsilon_{tk-1}xt=et+∑k=0∞0.3×0.6k εt−k−1
-
某WEAPON ( 2 , 2 ) \operatorname{WEAPON}(2,2)ARMA(2,2 ) Definition:Φ ( B ) xt = 3 + Θ ( B ) ε ı \Phi(B) x_{t}=3+\Theta(B) \varepsilon_{\imath};Φ ( B ) xt=3+Θ ( B ) e, 求 E ( x t ) E\left(x_{t}\right) E(xt) . Among them,ε t ∼ WN ( 0 , σ ε 2 ) \varepsilon_{t} \sim WN\left(0, \sigma_{\varepsilon}^{2}\right)et∼WN(0,pe2) ,Φ ( B ) = ( 1 − 0.5 B ) 2 . \Phi(B)=(1-0.5 B)^{2}.Φ ( B )=(1−0.5B)2 .
Θ ( B ) = ( 1 − 0.5 B ) 2 ⇒ ϕ 1 = 0.5 , ϕ 2 = − 0.25 E ( xt ) = ϕ 0 1 − ϕ 1 − ϕ 2 = 3 1 − 0.5 + 0.25 = 4 \begin{aligned } & \Theta(B)=(1-0.5 B)^{2} \Rightarrow \phi_{1}=0.5, \quad \phi_{2}=-0.25 \\ & E\left(x_{t}\ right)=\frac{\phi_{0}}{1-\phi_{1}-\phi_{2}}=\frac{3}{1-0.5+0.25}=4 \end{aligned}Θ ( B )=(1−0.5B)2⇒ϕ1=0.5,ϕ2=−0.25E(xt)=1−ϕ1−ϕ2ϕ0=1−0.5+0.253=4 -
Prove ARMA ( 1 , 1 ) \operatorname{ARMA}(1,1)ARMA(1,1 ) seqxt= 0.5 xt − 1 + ε t − 0.25 ε t − 1 , ε t ∼ WN ( 0 , σ ε 2 ) x_{t}=0.5 x_{t-1}+\varepsilon_{t}-0.25 \varepsilon_{t-1}, \varepsilon_{t} \sim WN\left(0, \sigma_{\varepsilon}^{2}\right)xt=0.5x _t−1+et−0.25 et−1,et∼WN(0,pe2) ’s autocorrelation coefficient is:
ρ k = { 1 , k = 0 0.27 , k = 1 0.5 ρ k − 1 , k ⩾ 2 \rho_{k}= \begin{cases}1, & k=0 \\ 0.27, & k=1 \\ 0.5 \rho_{k-1}, & k \geqslant 2\end{cases}rk=⎩ ⎨ ⎧1,0.27,0.5 pk−1,k=0k=1k⩾2
Denominator 1 = 1 2 , θ 1 = 1 4 \phi_{1}=\frac{1}{2}, \theta_{1}=\frac{1}{4}ϕ1=21,i1=41, according to ARMA ( 1 , 1 ) ARMA(1,1)ARMA(1,1 ) The recursive formula of the model Green function is:
G 0 = 1 G_{0}=1G0=1 ,
G 1 = ϕ 1 G 0 − θ 1 = 0.5 − 0.25 = ϕ 1 2 G_{1}=\phi_{1} G_{0}-\theta_{1}=0.5-0.25=\phi_{1} ^{2}G1=ϕ1G0−i1=0.5−0.25=ϕ12
G k = ϕ 1 G k − 1 = ϕ 1 k − 1 G 1 = ϕ 1 k + 1 , k ≥ 2 G_{k}=\phi_{1} G_{k-1}=\phi_{1}^ {k-1} G_{1}=\phi_{1}^{k+1}, k \geq 2Gk=ϕ1Gk−1=ϕ1k−1G1=ϕ1k+1,k≥2
ρ 0 = 1 \rho_{0}=1 r0=1
ρ 1 = ∑ j = 0 ∞ G j G j + 1 ∑ j = 0 ∞ G j 2 = ϕ 1 2 + ∑ j = 1 ∞ ϕ 1 2 j + 3 1 + ∑ j = 1 ∞ ϕ 1 2 ( j + 1 ) = ϕ 1 2 + ϕ 1 5 1 − ϕ 1 2 1 + ϕ 1 4 1 − ϕ 1 2 = ϕ 1 2 − ϕ 1 4 + ϕ 1 5 1 − ϕ 1 2 + ϕ 1 4 = 7 26 = 0.27 ρ k = ∑ j = 0 ∞ G j G j + k ∑ j = 0 ∞ G j 2 = ∑ j = 0 ∞ G j ( ϕ 1 G j + k − 1 ) ∑ j = 0 ∞ G j 2 = ϕ 1 ∑ j = 0 ∞ G j G j + k − 1 ∑ j = 0 ∞ G j 2 = ϕ 1 ρ k − 1 , k ≥ 2 \begin{aligned} & \rho_{1}=\frac{ \sum_{j=0}^{\infty} G_{j} G_{j+1}}{\sum_{j=0}^{\infty} G_{j}^{2}}=\frac{\ phi_{1}^{2}+\sum_{j=1}^{\infty} \phi_{1}^{2 j+3}}{1+\sum_{j=1}^{\infty} \ phi_{1}^{2(j+1)}}=\frac{\phi_{1}^{2}+\frac{\phi_{1}^{5}}{1-\phi_{1}^ {2}}}{1+\frac{\phi_{1}^{4}}{1-\phi_{1}^{2}}}=\frac{\phi_{1}^{2}}\ phi_{1}^{4}+\phi_{1}^{5}}{1-\phi_{1}^{2}+\phi_{1}^{4}}=\frac{7}{26 }=0.27 \\ & \rho_{k}=\frac{\sum_{j=0}^{\infty} G_{j} G_{j+k}}{\sum_{j=0}^{\infty} G_{j}^{2}}=\frac{\sum_{j=0}^{\infty} G_{j}\left(\phi_{1} G_{j+k-1}\right)}{\sum_{j=0}^{\infty} G_{j}^{2}}=\phi_{1} \frac{\sum_{j=0}^{\infty} G_{j} G_{j+k-1}}{\sum_{j=0}^{\infty} G_{j}^{2}}=\phi_{1} \rho_{k-1}, k \geq 2 \end{aligned}r1=∑j=0∞Gj2∑j=0∞GjGj+1=1+∑j=1∞ϕ12(j+1)ϕ12+∑j=1∞ϕ12 j + 3=1+1 − ϕ12ϕ14ϕ12+1 − ϕ12ϕ15=1−ϕ12+ϕ14ϕ12−ϕ14+ϕ15=267=0.27rk=∑j=0∞Gj2∑j=0∞GjGj+k=∑j=0∞Gj2∑j=0∞Gj( ϕ1Gj+k−1)=ϕ1∑j=0∞Gj2∑j=0∞GjGj+k−1=ϕ1rk−1,k≥2
Certification completed.
- For stationary time series, which of the following equations must be true?
(1) σ ε 2 = E ( ε 1 2 ) \sigma_{\varepsilon}^{2}=E\left(\varepsilon_{1}^{2}\right)pe2=E( e12)
(2) Cov ( y t , y t + k ) = Cov ( y t , y t − k ) \operatorname{Cov}\left(y_{t}, y_{t+k}\right)=\operatorname{Cov}\left(y_{t}, y_{t-k}\right) Those(yt,yt+k)=Those(yt,yt−k)
(3) ρ k = ρ − k \rho_{k}=\rho_{-k} rk=r−k
(4) y ^ t ( k + 1 ) = y ^ t + 1 ( k ) \widehat{y}_{t}(k+1)=\widehat{y}_{t+1}(k) y t(k+1)=y t+1(k).
(1) Established
(2) Established
(3) Established
(4) Established
- The annual firearm-related homicide death rate (per 100,000 people) in Australia from 1915 to 2004 is shown in the table.
(1) If the series is judged to be stationary, please determine which model in ARMA the stationary series has.
(2) If the sequence is judged to be non-stationary, please examine the stationarity and correlation characteristics of the sequence after first-order difference.
年 死亡率
1915 0.5215052
1916 0.4248284
1917 0.4250311
1918 0.4771938
1919 0.8280212
1920 0.6156186
1921 0.366627
1922 0.4308883
1923 0.2810287
1924 0.4646245
1925 0.2693951
1926 0.5779049
1927 0.5661151
1928 0.5077584
1929 0.7507175
1930 0.6808395
1931 0.7661091
1932 0.4561473
1933 0.4977496
1934 0.4193273
1935 0.6095514
1936 0.457337
1937 0.5705478
1938 0.3478996
1939 0.3874993
1940 0.5824285
1941 0.2391033
1942 0.2367445
1943 0.2626158
1944 0.4240934
1945 0.365275
1946 0.3750758
1947 0.4090056
1948 0.3891676
1949 0.240261
1950 0.1589496
1951 0.4393373
1952 0.5094681
1953 0.3743465
1954 0.4339828
1955 0.4130557
1956 0.3288928
1957 0.5186648
1958 0.5486504
1959 0.5469111
1960 0.4963494
1961 0.5308929
1962 0.5957761
1963 0.5570584
1964 0.5731325
1965 0.5005416
1966 0.5431269
1967 0.5593657
1968 0.6911693
1969 0.4403485
1970 0.5676662
1971 0.5969114
1972 0.4735537
1973 0.5923935
1974 0.5975556
1975 0.6334127
1976 0.6057115
1977 0.7046107
1978 0.4805263
1979 0.702686
1980 0.7009017
1981 0.6030854
1982 0.6980919
1983 0.597656
1984 0.8023421
1985 0.6017109
1986 0.5993127
1987 0.6025625
1988 0.7016625
1989 0.4995714
1990 0.4980918
1991 0.497569
1992 0.600183
1993 0.3339542
1994 0.274437
1995 0.3209428
1996 0.5406671
1997 0.4050209
1998 0.2885961
1999 0.3275942
2000 0.3132606
2001 0.2575562
2002 0.2138386
2003 0.1861856
2004 0.1592713
1. Convert data into time series variables and visualize them:
data <- read.table('./时间序列分析——基于R(第2版)习题数据/习题3.16数据.txt', header = TRUE, sep = "\t")
#将年份转换为时间序列类型
death <- ts(data$死亡率, start = c(1915), end = c(2004), frequency = 1)
#可视化
plot(death, type = "l", main = "1915-2004年澳大利亚枪支凶杀案死亡率",
xlab = "年份", ylab = "死亡率")
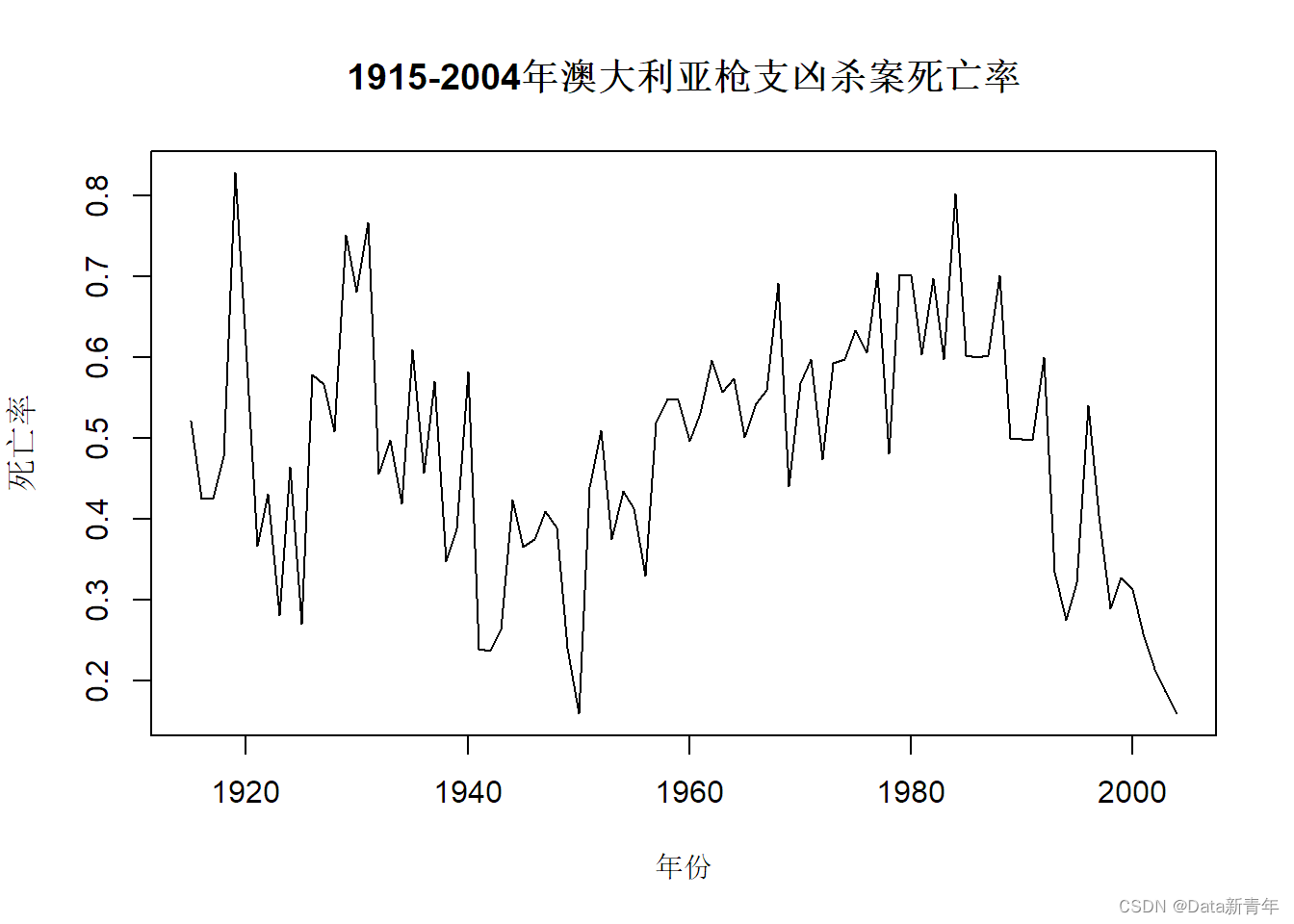
2. Perform a stationarity test on the time series:
library(tseries)
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
#进行ADF检验
adf.test(death)
##
## Augmented Dickey-Fuller Test
##
## data: death
## Dickey-Fuller = -1.2491, Lag order = 4, p-value = 0.8853
## alternative hypothesis: stationary
#进行KPSS检验
kpss.test(death)
## Warning in kpss.test(death): p-value greater than printed p-value
##
## KPSS Test for Level Stationarity
##
## data: death
## KPSS Level = 0.19826, Truncation lag parameter = 3, p-value = 0.1
Conclusion:
The p-value of the ADF test is greater than 0.05, and the null hypothesis cannot be rejected, that is, the sequence is not stationary; the
p-value of the KPSS test is less than 0.05, and the null hypothesis is rejected, that is, the sequence is not stationary.
3. Perform the first-order difference operation and perform the stationarity test again:
diff_ts <- diff(death)
#可视化
plot(diff_ts, type = "l", main = "差分后的1915-2004年澳大利亚枪支凶杀案死亡率",
xlab = "年份", ylab = "差分后的死亡率")
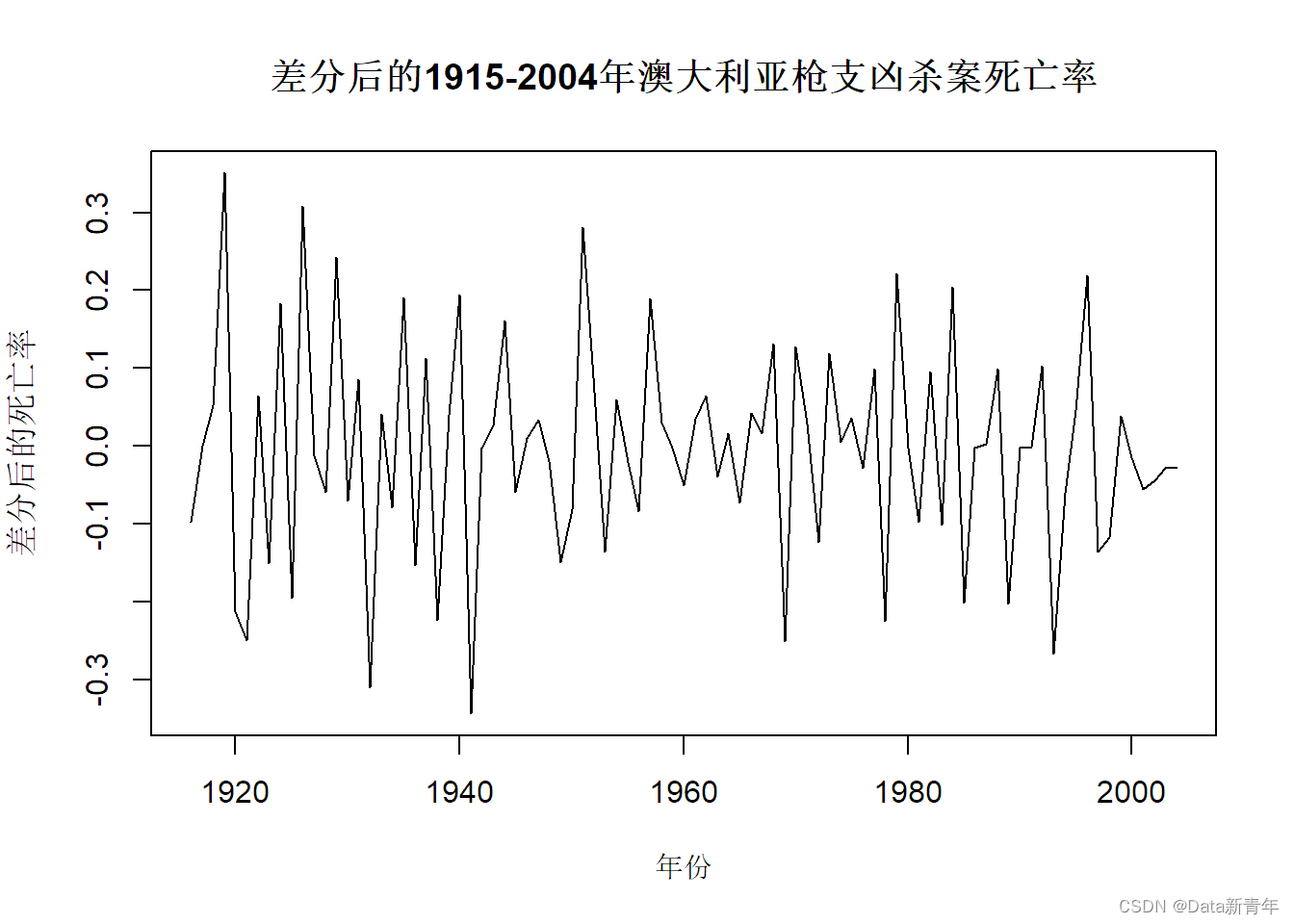
#进行ADF检验
adf.test(diff_ts)
## Warning in adf.test(diff_ts): p-value smaller than printed p-value
##
## Augmented Dickey-Fuller Test
##
## data: diff_ts
## Dickey-Fuller = -5.1026, Lag order = 4, p-value = 0.01
## alternative hypothesis: stationary
#进行KPSS检验
kpss.test(diff_ts)
## Warning in kpss.test(diff_ts): p-value greater than printed p-value
##
## KPSS Test for Level Stationarity
##
## data: diff_ts
## KPSS Level = 0.099305, Truncation lag parameter = 3, p-value = 0.1
Conclusion:
The sequence is significantly stationary after the first difference;
the p value of the KPSS test is greater than 0.05, and the null hypothesis cannot be rejected, that is, the sequence tends to be stationary under the first difference.
4. Perform ACF and PACF analysis on the first-differenced sequence to determine the ARMA model:
#ACF和PACF
par(mfrow = c(1,2))
acf(diff_ts, main = "ACF")
pacf(diff_ts, main = "PACF")
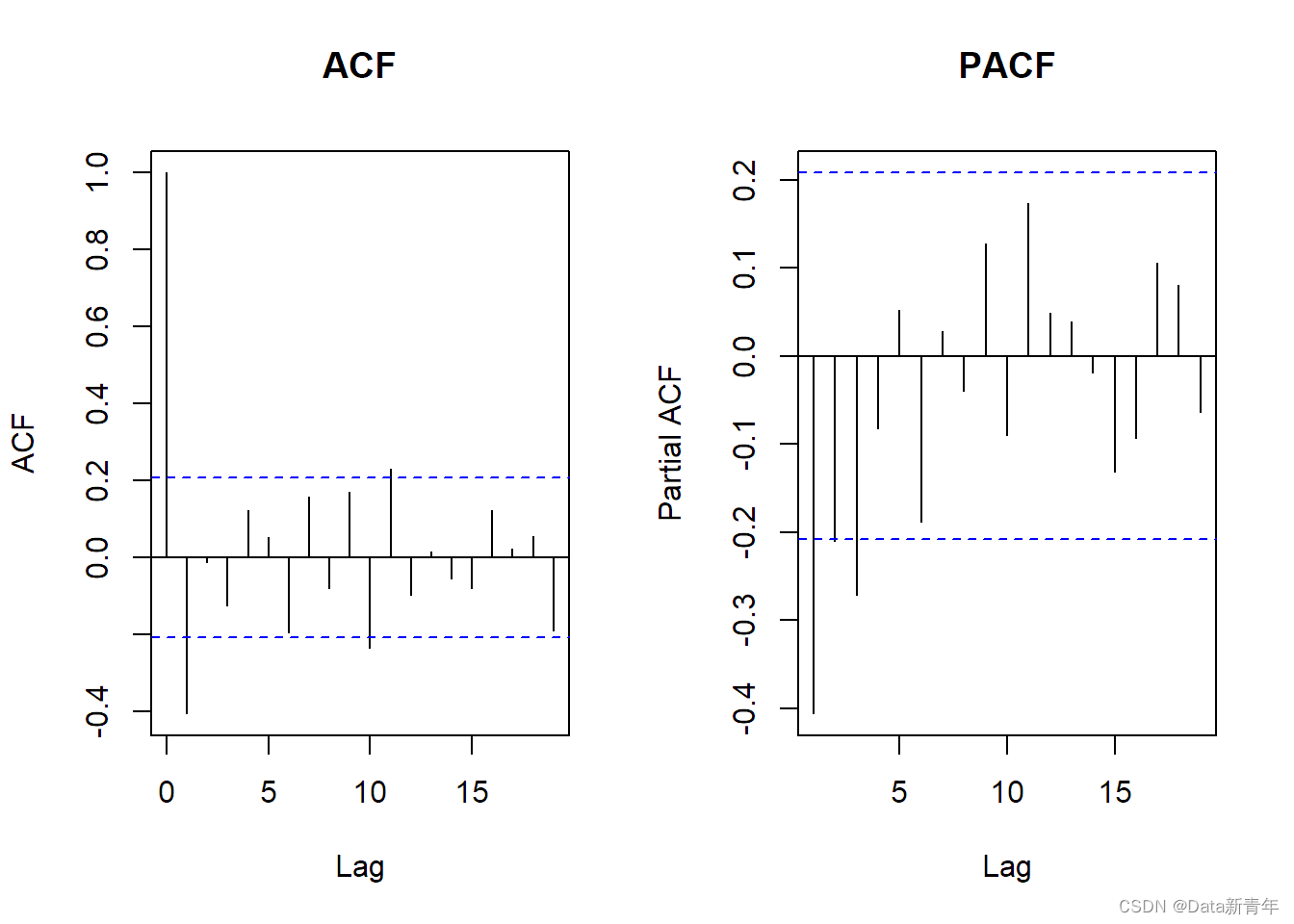
Conclusion:
ACF shows that the sequence has obvious adjacent lag autocorrelation, and PACF shows that the sequence has truncated autoregressive (AR) characteristics.
Therefore, one can choose the ARMA(p,0) model, where p takes a value of 2 or 3.
- The sequence of maximum monthly average water levels in Lake Michigan from 1860 to 1955 is shown in the table below.
(1) If the series is judged to be stationary, please determine which model in ARMA the stationary series has.
(2) If the sequence is judged to be non-stationary, please examine the stationarity and correlation characteristics of the sequence after first-order difference.
年 水位
1860 83.3
1861 83.5
1862 83.2
1863 82.6
1864 82.2
1865 82.1
1866 81.7
1867 82.2
1868 81.6
1869 82.1
1870 82.7
1871 82.8
1872 81.5
1873 82.2
1874 82.3
1875 82.1
1876 83.6
1877 82.7
1878 82.5
1879 81.5
1880 82.1
1881 82.2
1882 82.6
1883 83.3
1884 83.1
1885 83.3
1886 83.7
1887 82.9
1888 82.3
1889 81.8
1890 81.6
1891 80.9
1892 81
1893 81.3
1894 81.4
1895 80.2
1896 80
1897 80.85
1898 80.83
1899 81.1
1900 80.7
1901 81.1
1902 80.83
1903 80.82
1904 81.5
1905 81.6
1906 81.5
1907 81.6
1908 81.8
1909 81.1
1910 80.5
1911 80
1912 80.7
1913 81.3
1914 80.7
1915 80
1916 81.1
1917 81.87
1918 81.91
1919 81.3
1920 81
1921 80.5
1922 80.6
1923 79.8
1924 79.6
1925 78.49
1926 78.49
1927 79.6
1928 80.6
1929 82.3
1930 81.2
1931 79.1
1932 78.6
1933 78.7
1934 78
1935 78.6
1936 78.7
1937 78.6
1938 79.7
1939 80
1940 79.3
1941 79
1942 80.2
1943 81.5
1944 80.8
1945 81
1946 80.96
1947 81.1
1948 80.8
1949 79.7
1950 80
1951 81.6
1952 82.7
1953 82.1
1954 81.7
1955 81.5
1. Convert data into time series variables and visualize them:
data <- read.table('./时间序列分析——基于R(第2版)习题数据/习题3.17数据.txt', header = TRUE, sep = "\t")
#将年份转换为时间序列类型
level <- ts(data$水位, start = c(1860), end = c(1955), frequency = 1)
#可视化
plot(level, type = "l", main = "1860-1955年密歇根湖每月平均水位变化",
xlab = "年份", ylab = "水位")
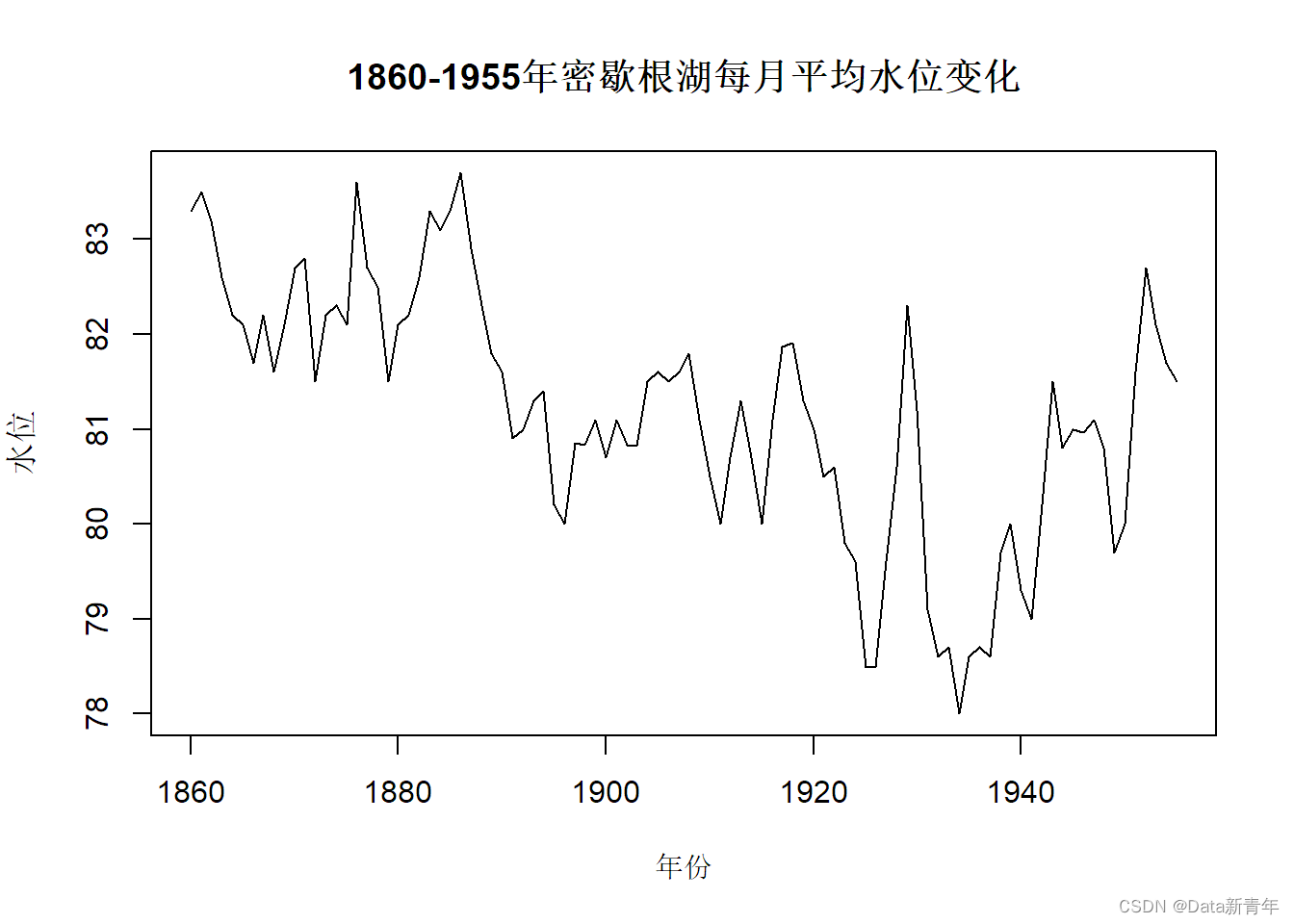
2. Perform a stationarity test on the time series:
library(tseries)
#进行ADF检验
adf.test(level)
##
## Augmented Dickey-Fuller Test
##
## data: level
## Dickey-Fuller = -2.3833, Lag order = 4, p-value = 0.4181
## alternative hypothesis: stationary
#进行KPSS检验
kpss.test(level)
## Warning in kpss.test(level): p-value smaller than printed p-value
##
## KPSS Test for Level Stationarity
##
## data: level
## KPSS Level = 1.3798, Truncation lag parameter = 3, p-value = 0.01
Conclusion:
The p-value of the ADF test is greater than 0.05, and the null hypothesis cannot be rejected, that is, the sequence is not stationary; the
p-value of the KPSS test is less than 0.05, and the null hypothesis is rejected, that is, the sequence is not stationary.
3. Perform the first-order difference operation and perform the stationarity test again:
diff_le <- diff(level)
#可视化
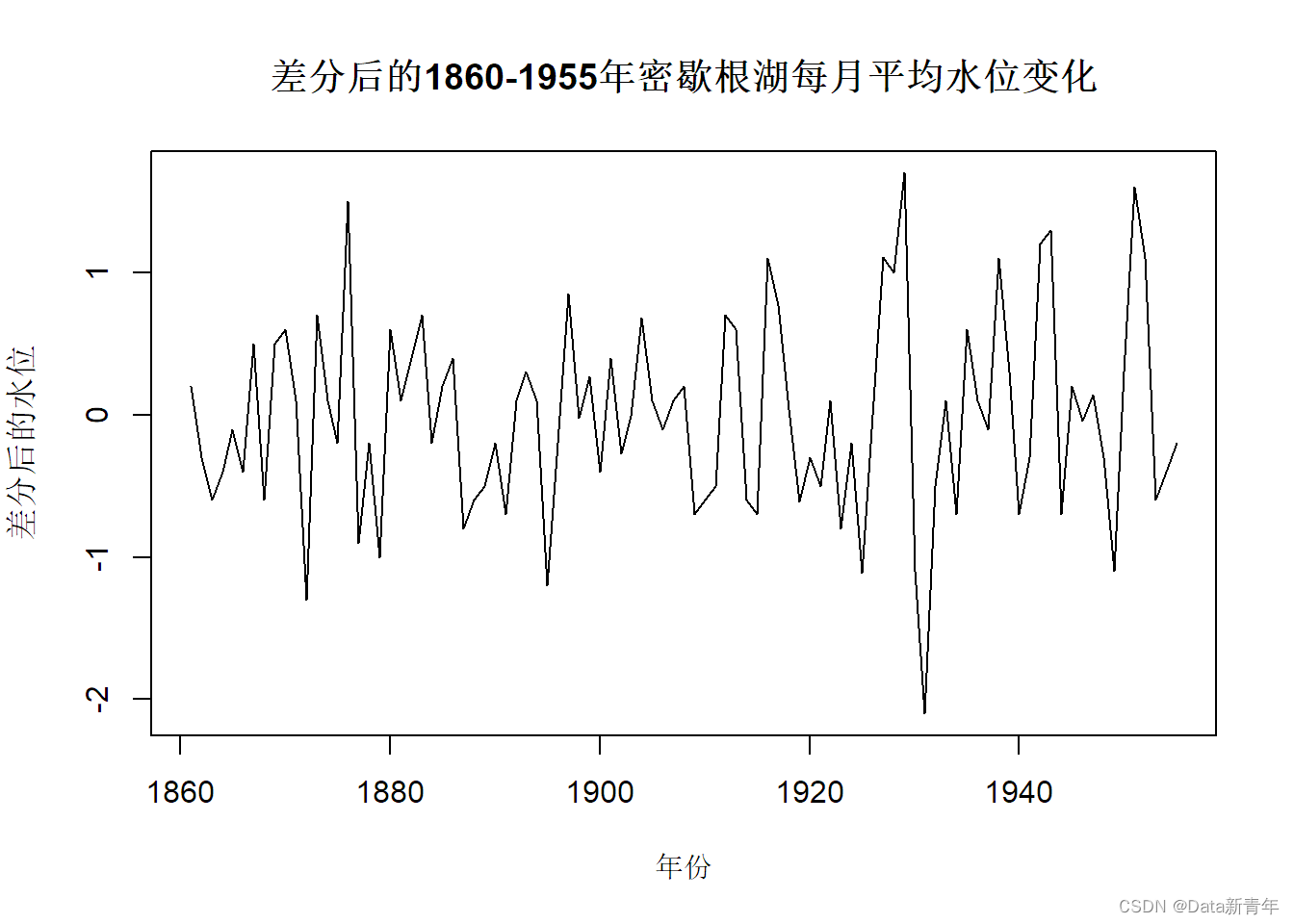
plot(diff_le, type = "l", main = "差分后的1860-1955年密歇根湖每月平均水位变化",
xlab = "年份", ylab = "差分后的水位")
#进行ADF检验
adf.test(diff_le)
## Warning in adf.test(diff_le): p-value smaller than printed p-value
##
## Augmented Dickey-Fuller Test
##
## data: diff_le
## Dickey-Fuller = -5.6057, Lag order = 4, p-value = 0.01
## alternative hypothesis: stationary
#进行KPSS检验
kpss.test(diff_le)
## Warning in kpss.test(diff_le): p-value greater than printed p-value
##
## KPSS Test for Level Stationarity
##
## data: diff_le
## KPSS Level = 0.07181, Truncation lag parameter = 3, p-value = 0.1
Conclusion:
The sequence is significantly stationary after the first difference;
the p value of the KPSS test is greater than 0.05, and the null hypothesis cannot be rejected, that is, the sequence tends to be stationary under the first difference.
4. Perform ACF and PACF analysis on the first-differenced sequence to determine the ARMA model:
#ACF和PACF
par(mfrow = c(1,2))
acf(diff_le, main = "ACF")
pacf(diff_le, main = "PACF")
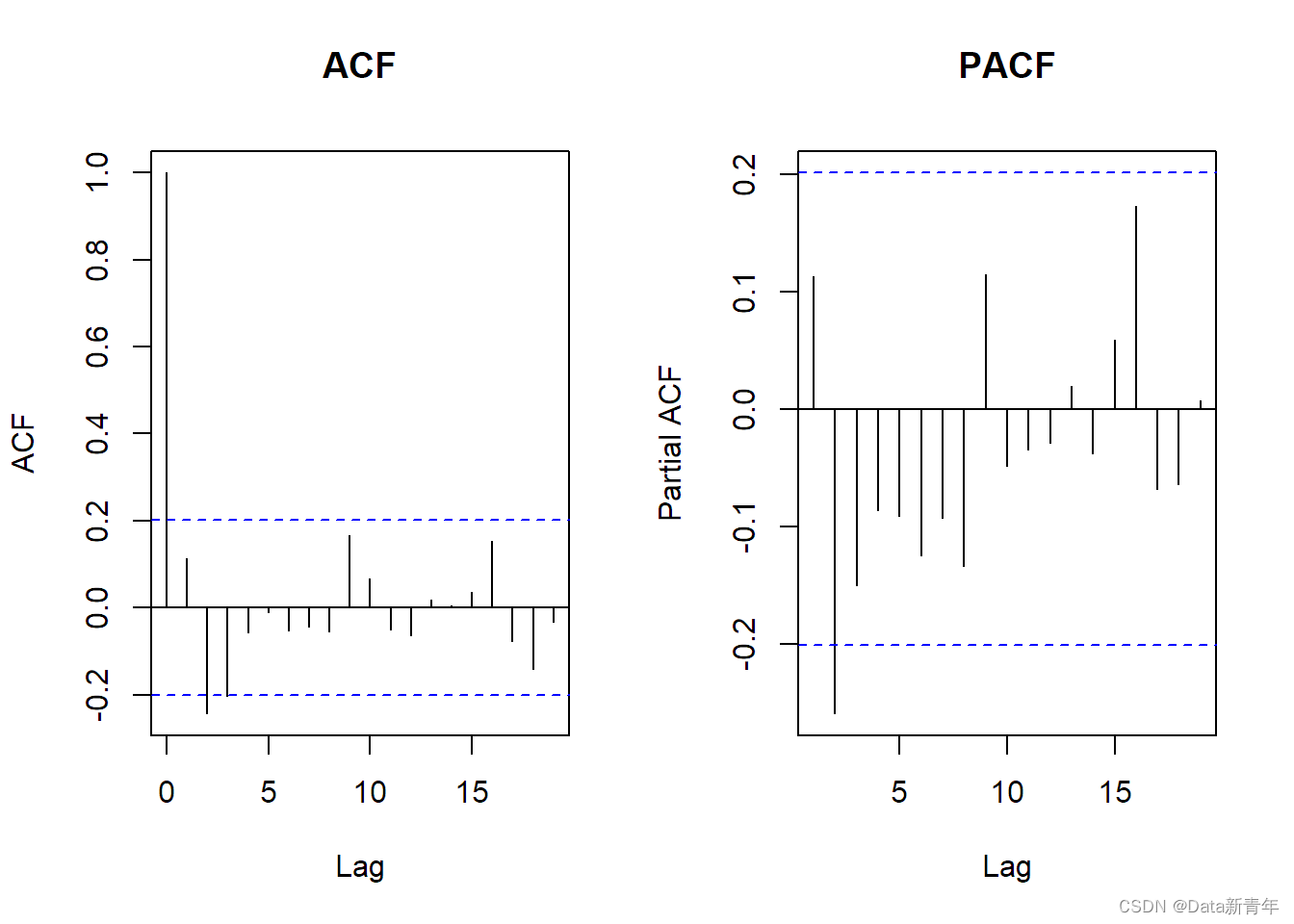
By performing ACF and PACF analysis on the sequence after first difference.
The ACF plot slowly decays from lags=1, indicating that an AR(1) model may be suitable for this sequence. But as the lag gets larger, the ACF gets closer and closer to 0, which means that a MA(1) model may also be suitable.
The PACF plot is censored at lags=1, indicating that an AR(1) model may be suitable. However, at lags=2, PACF is significantly negative again, which indicates that an MA(1) term may be needed to explain the sequence.
It can be seen that the ARMA(1,1) model may be a more suitable model feature.