[AI Drawing Study Notes] Probabilistic Diffusion Model Probabilistic Diffusion Model

Reference: Probabilistic Diffusion Model Probabilistic Diffusion Model Theory and Detailed Interpretation of the Complete PyTorch Code
Understand the Diffusion Model from the simplest to the deeper

---

Review VAE

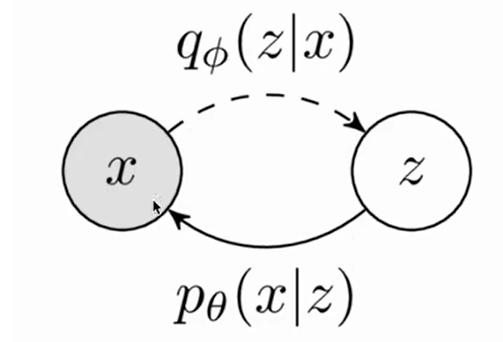
In the previous section, we learned about the principle of VAE. Generally speaking, it can be divided into two processes. One is to use $q(z|x)$ gives the Encoder the process of forward learning, and the other is to use$p(x|z)$ gives the Decoder the process of reverse reasoning.

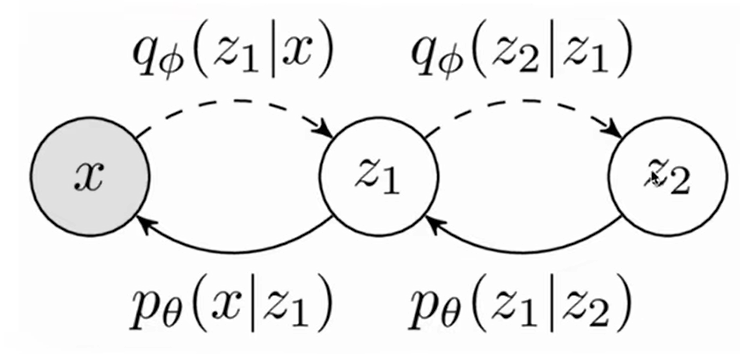
The multi-layer VAE model is actually similar to the single-layer VAE, except that on a single-layer basis, we regard it as a Markov chain, so each probability is only related to the previous probability. The above is where

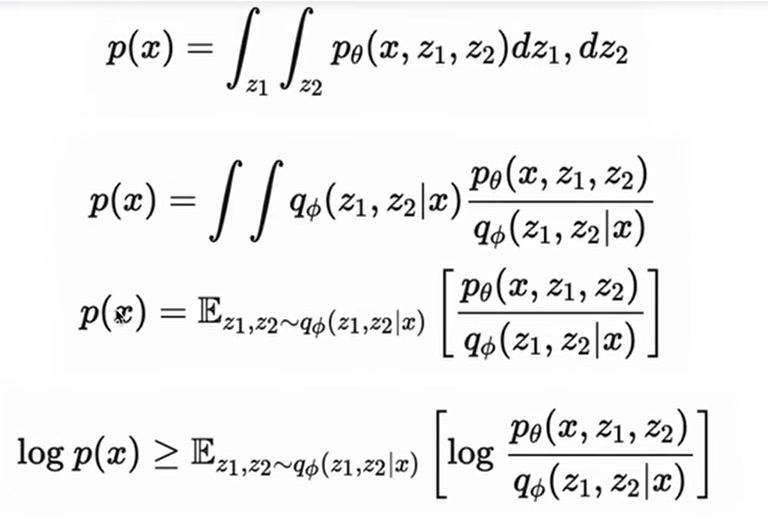
we use Jensen The confidence lower bound obtained by the inequality.

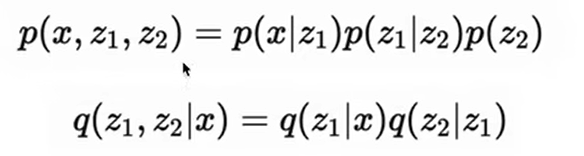
The above is the chain rule of probability (under the Markov chain). We substitute this into the maximum likelihood above, and we can get that the lower bound can be written in this form: This is the objective

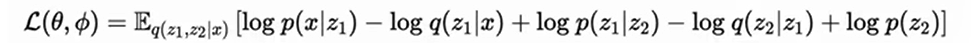
function of the multi-layer VAE.

---

Diffusion Model

The reason why I want to introduce VAE first is because the process of multi-layer VAE is actually very similar to the Diffusion Model.

The principle of Diffusion Model is to first target $x_0$Step by step forward noise is added to obtain the final distribution $x_T$, and then use the process of reverse reasoning to gradually denoise, by $x_T$Get $x_0$。

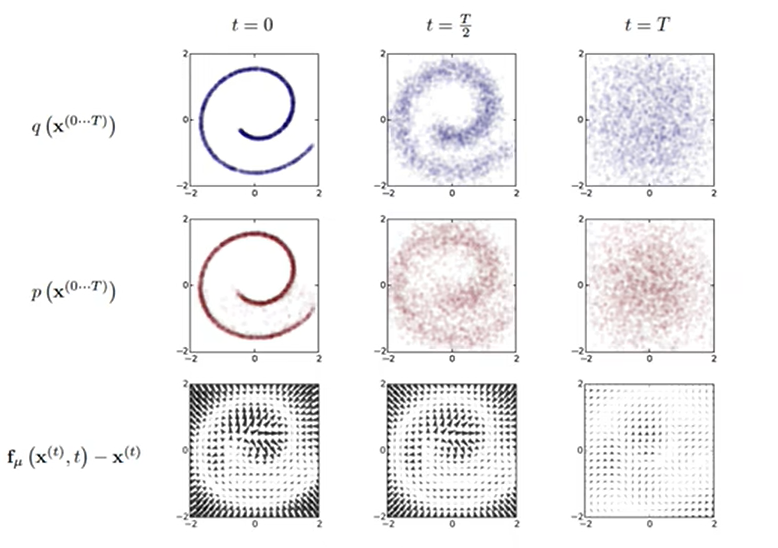
The above picture is the visualization process of Diffusion Model. In general, it is the diffusion process of adding noise (entropy increase process) $q(x_t|x_{t-1})$ , which is the first line of the above figure, we can see that the image gradually becomes disordered as the noise is added.
For a given noise picture$x_T$, the Diffusion Model learned the reverse reasoning process of denoising $p(x_{t-1}|x_t)$ , you can generate a new picture, which is the second line of the above picture. (from T time to 0 time) you can see that we have produced a new sample, which is roughly the same as the original training picture we used to add noise. are similar.
The third line is the drift amount, from which we can see the direction of image pixel movement at the previous moment and the next moment.

---

Diffusion process forward

1. Given the initial data distribution $x_0\sim q\left(x\right)$ , Gaussian noise (affine transformation) can be continuously added to the original distribution, and the standard deviation of this noise is a fixed value$b_t$Determined, the mean (expected) is at a fixed value $b_t$and current ttData at time$t$$x_t$Decide. This process is a Markov chain.

2.With $As\; t$ continues to increase, the final data distribution$x_T$It becomes a Gaussian distribution that is independent in each direction.

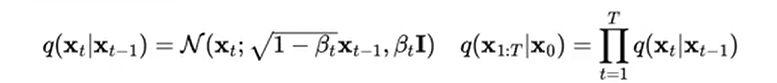
About $x_t$The algorithm that obeys the Gaussian distribution is actually the resampling technique we talked about in the previous section. We sample a $z$ , then calculate$x=\sigma z\_+\mu$ gets$The\; sample\; value\; of\; x$ . Use resampling techniques to$x_{t-1}$You can find xt x_t by iterating$x_t$Gaussian distribution. And $q(x_t|x_0)$ satisfies the Markov chain.

Note: $b_t\in (0,1)$ , and will grow larger over time.

3. q ( xt ) q(x_t) at any time$q\left(x_t\right)$ derivation can also be based entirely on$x_0$and $b_t$To calculate without iteration, the following is the calculation process:

Here we need to use the parameter renormalization technique , we let $a_t=1-b_t，{\overline{a}}_t=\prod _{t=1}^T{a}_i$, then change the above formula $q(x_t|x_{t-1})$ into the resampling technique$x_t=\sigma z{\_}_{t-1}+m=\sqrt{b}{z}_{t-1}+\sqrt{1-b}{x}_{t-1}$get:

$x_t=\sqrt{a_t}{x}_{t-1}+\sqrt{1-a_t}{z}_{t-1}{z}_{t-1},z_{t-2}average...\sim N(0,I)$

We will xt − 1 x_{t-1} in the above formula$x_{t-1}$Use about $x_{t-2}$的式子替换：
$$\begin{gathered} x_t=\sqrt{a_t}(\sqrt{a_{t-1}}{x}_{t-2}+\sqrt{1-a_{t-1}}{z}_{t-2})+\sqrt{1-a_t}{z}_{t-1} \\ =\sqrt{a_t{a}_{t-1}}{x}_{t-2}+\sqrt{a_t-a_t{a}_{t-1}}{z}_{t-2}+\sqrt{1-a_t}{z}_{t-1} \end{gathered}$$

Give a basic conclusion ( independent distribution additivity ): two normal distributions $X\sim N(m_1,p_1^2)sumY\sim N(m_2,p_2^2)$ obtained superposition distribution$aX+The\; mean\; of\; bY$ is$a{\mu }_1+b\mu {\_}_2$,Equally $a^2{p}_1^2+b^2{p}_2^2$，所以$\sqrt{a_t-a_t{a}_{t-1}}{z}_{t-2}+\sqrt{1-a_t}{z}_{t-1}$Yuz $z\sim N(0,I)$ , so the corresponding superposition distribution mean is$m=0+0=0$，方差$p^2=a^2+b^2=a_t-a_t{a}_{t-1}+1-a_t=1-a_t{a}_{t-1},$ so substituting into the resampling formula is$\sigma z\_+m=\sqrt{1-a_t{a}_{t-1}}z$

$$\begin{gathered} x_t=\sqrt{a_t{a}_{t-1}}{x}_{t-2}+\sqrt{1-a_t{a}_{t-1}}{\overline{z}}_{t-2}({\overline{z}}_{t-2}is\; a\; mixture\; of\; Gaussians,\; but\; still\; a\; standard\; normal\; distribution) \\ =... \\ =\sqrt{{\overline{a}}_t}{x}_0+\sqrt{1-{\overline{a}}_t}z \end{gathered}$$

结论：
$x_t=\sqrt{{\overline{a}}_t}{x}_0+\sqrt{1-{\overline{a}}_t}z(3)$

Therefore, q (xt) q(x_t) at any time$q(x_t)$ can be based on$x_0$and $b_t$to calculate without iteration:

$q(x_t|x_0)=N(x_t;\sqrt{{\overline{a}}_t}{x}_0,(1-{\overline{a}}_t)I)$ , so that we can sample$x_t$There is no need for t iterations.

So $\alpha$ is more of a learning rate-like parameter, since$\beta$ will become larger and larger, so$\alpha$ will become smaller and smaller, so after enough moments$\sqrt{a}\to 0,\sqrt{1-a}\to 1$ , so when time t is reached,$q(x_t|x_0)=N(x_t;0,I)$ will converge to a standard normal distribution, so that we can find the maximum time$t$ ._ The property expressed in terms of learning rate is that if$x_t$Predict $x_0$, the generation in the previous stages will quickly show the bottom of the image, and the later it will be slower, the more details need to be generated.

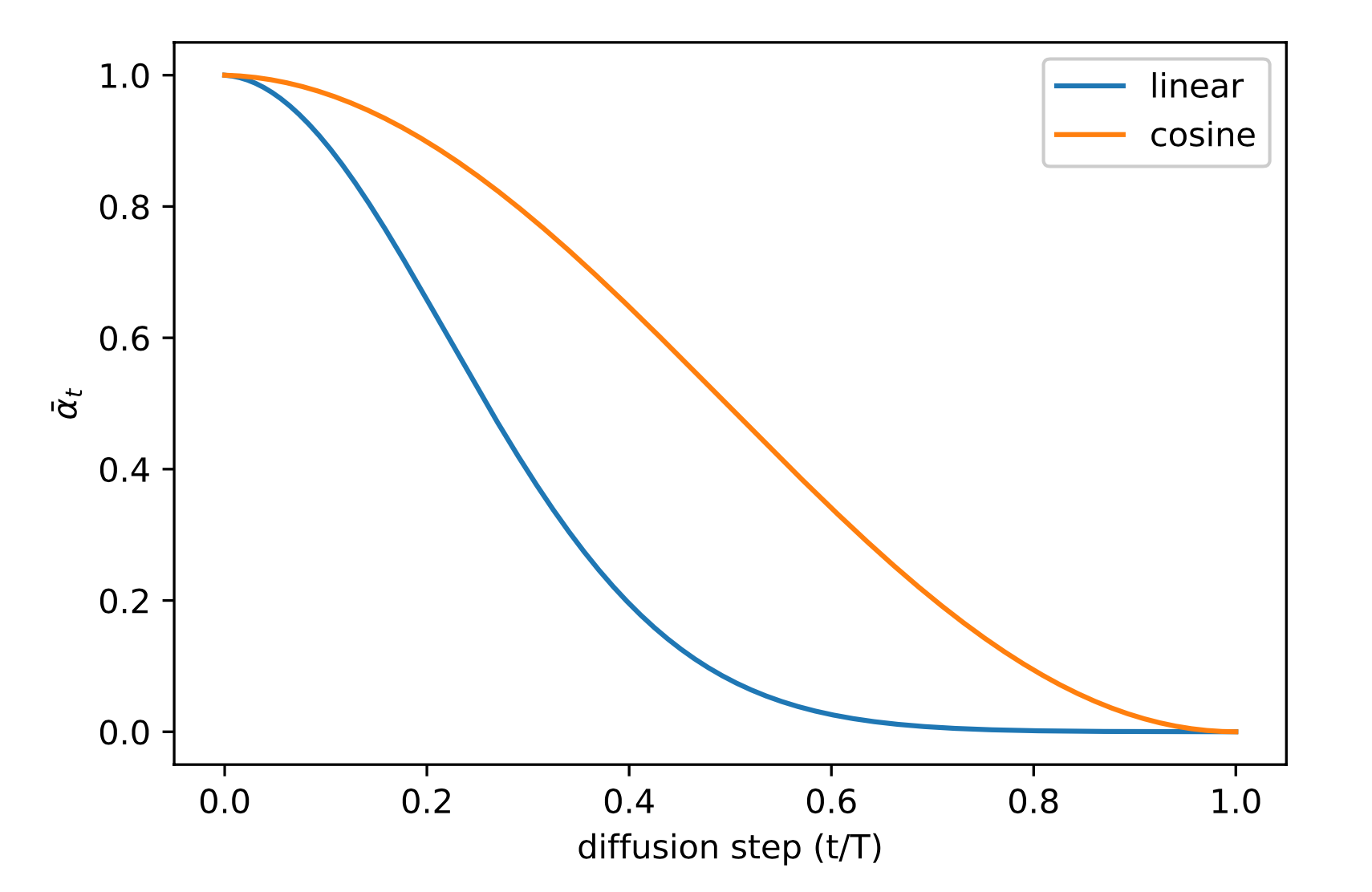
(The above figure represents ${\bar{a}}_t$relationship with the diffusion step)

From here we can see some differences between Diffusion Model and VAE.
First, in VAE, the parameters are predicted through the forward and reverse process, but in diffusion, a fixed parameter is given for training. Secondly, the hidden variable zz
sampled in VAE$z$ and$x$ is related to a certain extent, and xt x_tin diffusion$x_t$The end result is a standard normal distribution, and $x$ is irrelevant.
Also in VAE$xwazz$ _$The\; dimensions\; of\; z$ are not necessarily the same, and in diffusion$x_0....x_t$The dimensions are always the same.

---

reverse diffusion process

If the forward process is a process of adding noise, then the reverse process is a process of denoising inference. If we can gradually obtain the reversed distribution $q(x_{t-1}|x_t)$ , you can get from the standard normal distribution$x_t\sim N(0,I)$ Restore the original image distribution$x_0$, it is proved in Document ^{1 that if} $q(x_{t-1}|x_t)$ satisfies Gaussian distribution and$b_t$Small enough, then $q(x_{t-1}|x_t)$ is still a Gaussian distribution, if xt . . . x 0 x_t...x_0is gradually$x_t...x_0$It is really difficult to calculate by fitting to find the Gaussian distribution parameters it obeys. So we need to construct a parameter distribution for estimation, and the reverse diffusion process is still a Markov chain.

We use a deep learning model (parameters are $\theta$ , the current mainstream is the structure of U-Net+attention) to predict such an inverse distribution$p_{}$. (Similar to VAE):

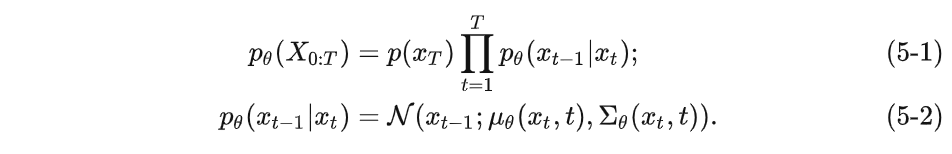
Although we cannot get the reversed distribution $q(x_{t-1}|x_t)$ , but if we know$x_0$, can be calculated by the following formula:

$q(x_{t-1}|x_t,x_0)=N(x_{t-1};\tilde{m}(x_t,x_0),{\tilde{b}}_{t}I)(6)$

The reasoning is as follows:

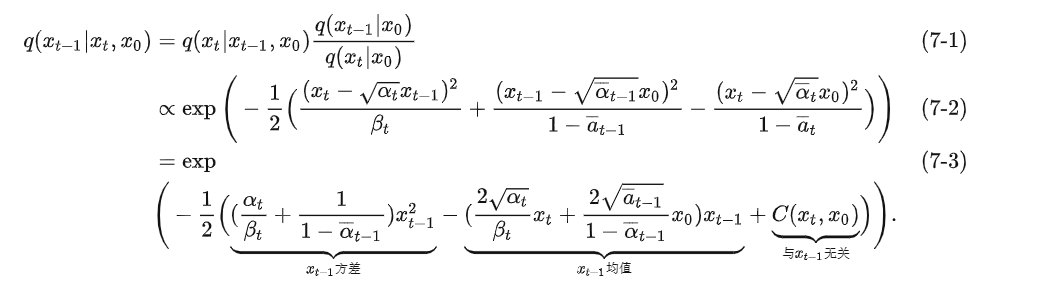
We use Bayes’ formula to reason about (7-1):
$q(a|b,c)=\frac{q(a,b,c)}{q(b,c)}$
Among them, the chain rule $q(a,b,c)=q(b|a,c)q(a|c)q(c)$，$q(b,c)=q(b|c\left)q\right(c)$
Therefore, substitute the original formula$=\frac{q(b|a,c)q(a|c)q(c)}{q(b|c)q(c)}=\frac{q(b|a,c)q(a|c)}{q(b|c)}$, since it is a Markov chain, the above formula is also equivalent to $q(b|c)\frac{q(a|c)}{q(b|c)}$

We can see that in equation (7-1), we use Bayes' formula to transform this reverse process into a forward process, and (7-2) is its corresponding Gaussian distribution probability density function. We expand it to get formula (7-3), where $x_{t-1}$Irrelevant terms include only $x_t\&x_0$The items are classified into $C(x_t,x_0)$

( The probability density function of the Gaussian distribution is $f(x)=\frac{1}{\sqrt{2p.m}p}{e}^{-\frac{(x-\mu {)}^2}{2p^2}}$)

We said before that $q(x_{t-1}|x_t)$ is still a Gaussian distribution, which means that the above formula can be organized into the formula of a Gaussian distribution, and the corresponding exponential part of the general Gaussian probability density function is$exp(-\frac{(x-\mu {)}^2}{2p^2})=exp(-\frac{1}{2}(\frac{1}{p^2}{x}^2-\frac{2}{p^2}x+\frac{m^2}{p^2}))$ , which corresponds to the form compiled in (7-3), therefore:

Use the β \beta mentioned in the forward direction$\beta$ replaces the variance$p^2$ , get:

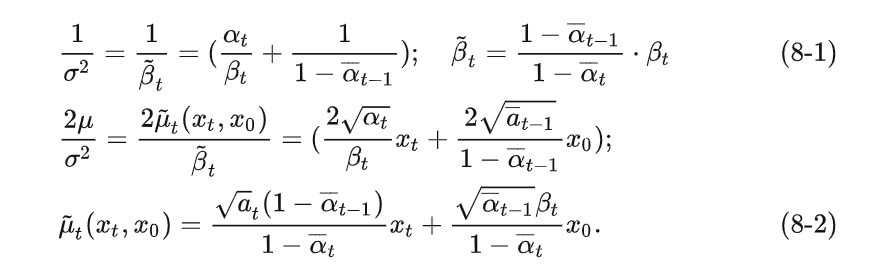
Due to the inference 3 mentioned in the diffusion process, we know that xt x_t at any time$x_t$Can be determined by $x_0$and $\beta$ means. therefore:

$x_0=\frac{1}{\sqrt{{\bar{a}}_t}}(x_t-\frac{b_t}{\sqrt{1-{\bar{a}}_t}}{\bar{z}}_t)$($x_t$(formula deformation)

Substituting this into (8-2) we get

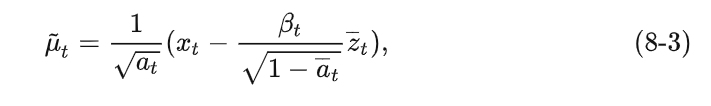
The Gaussian distribution ${\bar{z}}_t$The noise predicted by the depth model (used for denoising) can be viewed as $z_{}(x_t,t),$ get:

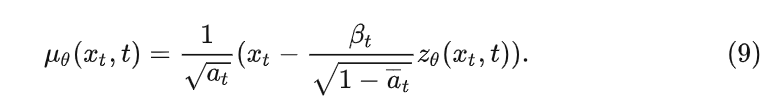
After a series of calculations, we first get $q(x_{t-1}|x_t)$ of the Gaussian distribution probability density function, and then organize it into the general form of the exponential part of the Gaussian distribution, thereby obtaining the corresponding mean and variance, where the variance$\beta$ is a constant value, and the mean$\mu$ is then expressed as$x_t,t$ is the function form of the parameter

In this way, the inference of each step of DDPM can be summarized as:

1) Each time step passes $x_t$andtt $t$ to predict Gaussian noise$z_{}(x_t,t)$ , and then the mean$m_{}(x_t,t)$

2) Get the variance $S_{}(x_t,t)$,DDPM中使用untrained $S_{}(x_t,t)={\tilde{b}}_t$(That is, the training variance is not used as a fixed parameter), and it is considered that ${\tilde{b}}_t=b_t$和${\tilde{b}}_t=\frac{1-{\bar{a}}_{t-1}}{1-{\bar{a}}_t}\cdot b_t$Approximate results

3) According to (5-2), we get $q(x_{t-1}|x_t)$,利用重参数技巧得到$x_{t-1}$

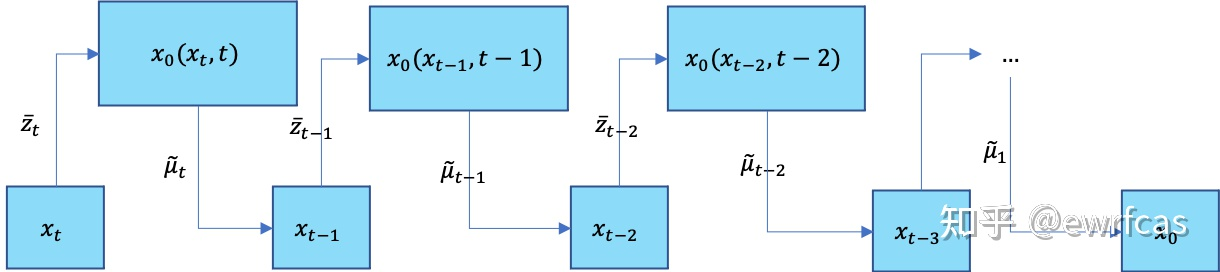
重复上述步骤逐步去噪，直到计算出$x_0$,去噪过程完毕。

---

Diffusion训练

讲完了前向加噪的扩散过程和逆向去噪的推断过程（虽然文字上来看原理很简单，但是公式好繁杂）。现在我们讲讲如何训练diffusion model以得到靠谱的参数${\mu }_{\theta }(x_t,t)和{\Sigma }_{\theta }(x_t,t)$，方法还是最大对数似然（此处用的最小化负对数似然）。

由于整个Diffusion模型和VAE很相似，训练过程也是，由于KL散度恒大于0，因此我们在负对数似然上加上一个KL散度就构成了它的上界（和VAE最大对数似然的时候正好相反，那时是减去一个KL散度是下界)：

利用詹森不等式，我们就能得到（这块看的不太细，记住结论就好)：

我们进一步对$L_{VLB}$进行推导，可以得到熵与多个KL散度的累加²，其中分母是扩散过程，分子是逆扩散过程：

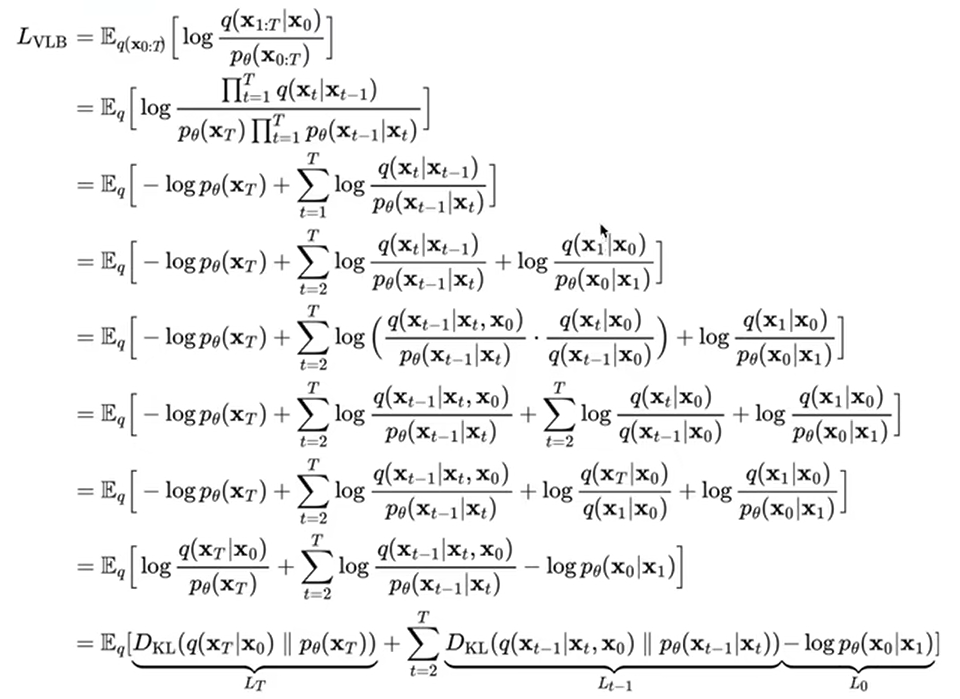
（上式【从$L_{VLB}$开始为第一行】第四行到第五行又是应用了贝叶斯公式，先逆向马尔科夫链补上了一个$x_0$再应用了和之前前向中讲到的一模一样的贝叶斯公式)
第六行的第三项${\sum }_{t=2}^{T}log\frac{q(x_t|x_0)}{q(x_{t-1}|x_0)}$可化简,最后与第四项以及第一项可合并，最终得到了第七行的式子

最后一行将其简化为了含有KL散度的式子，其中$L_T$不含参（q分布不含参，$x_T$逆向过程最终为纯高斯噪声)相当于常量可以直接忽略，$L_{t-1}$是逆扩散过程的KL散度，最后考虑的还是$L_{t-1}和L_0$。

并且由于$q和p_{\theta }$其实都是高斯分布，并且$q$是关于参数${\beta }_t$的高斯分布，且${\beta }_t$是untrained的固定参数(忘记的,点此回去)，$p_{\theta }$的高斯分布均值是${\mu }_{\theta }$,方差是${\Sigma }_{\theta }$且${\Sigma }_{\theta }$也是untrained的固定参数。因此可训练的参数$\theta$只在$p_{\theta }$中。

上面刚才推导的式子也可写为：

给出一个结论：对于两个高斯分布p，q而言，它们的KL散度可等价为
$D_{KL}(p,q)=log\frac{{\sigma }_2}{{\sigma }_1}+\frac{{\sigma }_1^2+({\mu }_1-{\mu }_2{)}^2}{2{\sigma }_2^2}-\frac{1}{2}$
让我们把$L_{t-1}$的式子用上式表示出来，得到:

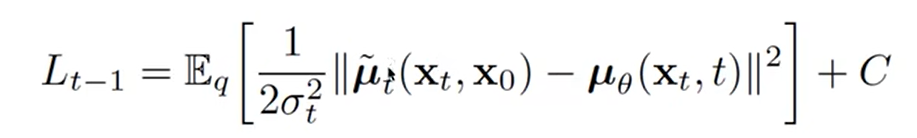
(此处$L_{t-1}$应该是笔误，实为$L_t$，$L_{VLB}$给出的是$t=2$开始，在(14-3)中已经被改为$t=1$开始到$T-1$)

然后将${\tilde{\mu }}_t$用(8-2)替换，${\mu }_{\theta }$用(9)替换，$x_t$用(3)替换，得到：

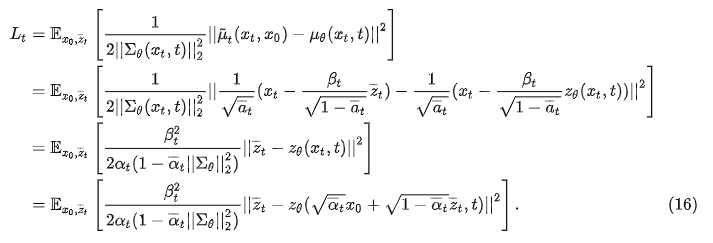
从(16)可以看出，diffusion训练的核心就是取学习高斯噪声${\bar{z}}_t,z_{\theta }$之间的均方误差MSE。论文中作者说我们可以将(16)式子中前面的这个系数给直接丢掉，这样训练会更稳定。

最后论文给出的式子，我们将${\bar{z}}_t$替换为$ϵ$，$z_{\theta }$替换为${ϵ}_{\theta }$,DDPM将loss进一步简化为：

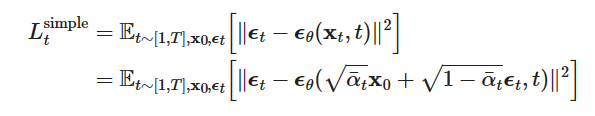
训练过程可以看做：

1）获取输入$x_0$，从1…T随机采样一个$t$
2) 从标准高斯分布采样一个噪声$ϵ\sim N(0,I)$
3) 最小化loss函数

---

总结

最后我们给出DDPM提供的训练/测试（采样）流程图

在训练过程中，我们要输入$x_0$进行随机采样时刻$t$并采样噪声$ϵ$，然后对loss函数进行梯度下降直到拟合。而在测试采样过程中，我们则利用马尔科夫链逆向逐步去噪计算$x_T$直到$x_0$作为最后的生成结果。

---

加速Diffusion采样和方差的选择(DDIM)

通过遵循反向扩散过程的马尔可夫链从DDPM生成样品非常慢，因为高质量生成需要的$T$最多要走一千步或是几千步。“例如，从 DDPM 采样大小为 20 × 50 的 32k 图像大约需要 32 小时，但从 Nvidia 2080 Ti GPU 上的 GAN 采样不到一分钟。”
这就导致diffusion的前向过程非常缓慢。在denoising diffusion implicit model (DDIM)中提出了一种牺牲多样性来换取更快推断的手段。

一种简单的方法是运行一个跨步的采样，通过每隔$\lceil T/S\rceil$步进行采样更新，总共采样$S$步，这样就能有效减少采样数量。

另一种方法是重写$q_{\sigma }(x_{t-1}|x_t,x_0)$的标准差${\sigma }_t$：
根据(3)我们可知：

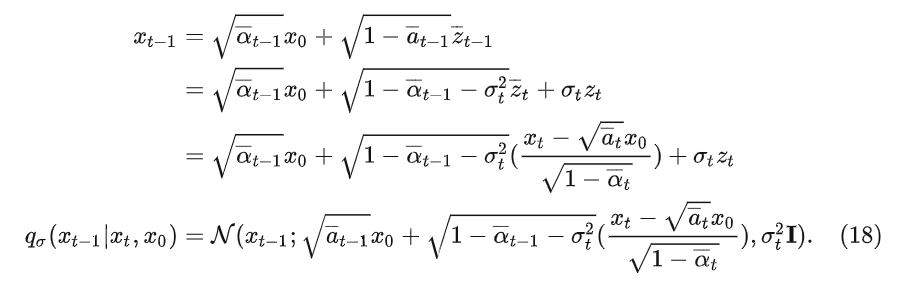
（第二步利用了独立高斯分布可加性)

最终得到的(18)将方差${\sigma }_t^2$迎入到了均值中，当${\sigma }_t^2={\tilde{\beta }}_t=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}$时，(18)等价于(6)。我们给定一个$\eta$作为控制采样随机性的超参数${\sigma }_t^2=\eta {\tilde{\beta }}_t$（作用类似于调整方差的大小),当$\eta =1$的时候就等价于DDPM，当$\eta =0$的时候是DDIM

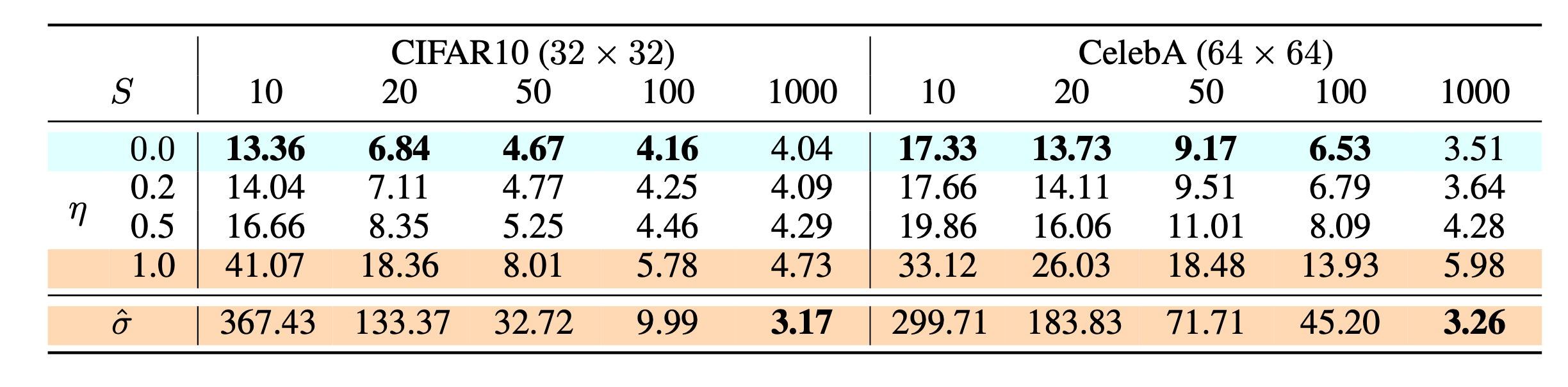
（上图是不同设置的扩散模型在 CIFAR10 和 CelebA 数据集上的 FID 得分，包括了DDIM($\eta =0$)以及DDIM($\hat{\sigma }$)($\eta =1$））

根据上表可知，数据量较小时DDIM的训练更快，而数据量较大时使用DDPM并采用更大的方差效果更好

与DDPM相比，DDIM能够：

1.使用更少的步骤生成更高质量的样本。
2.具有“一致性”属性，因为生成过程是确定性的，这意味着以同一潜在变量为条件的多个样本应该具有类似的高级特征。
3.由于一致性，DDIM 可以在潜在变量中执行语义上有意义的插值。

---

1. Feller, William. “On the theory of stochastic processes, with particular reference to applications.” Proceedings of the [First] Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, 1949. ↩︎

2. Feller, William. “On the theory of stochastic processes, with particular reference to applications.” Proceedings of the [First] Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, 1949. ↩︎