Algorithm and Data Structure Interview Guide - Edit Distance Question

Edit distance problem

Edit distance, also known as Levenshtein distance, refers to the minimum number of modifications required to convert two strings into each other. It is usually used to measure the similarity of two sequences in information retrieval and natural language processing.

!!! question

输入两个字符串 $s$ 和 $t$ ，返回将 $s$ 转换为 $t$ 所需的最少编辑步数。

你可以在一个字符串中进行三种编辑操作：插入一个字符、删除一个字符、替换字符为任意一个字符。

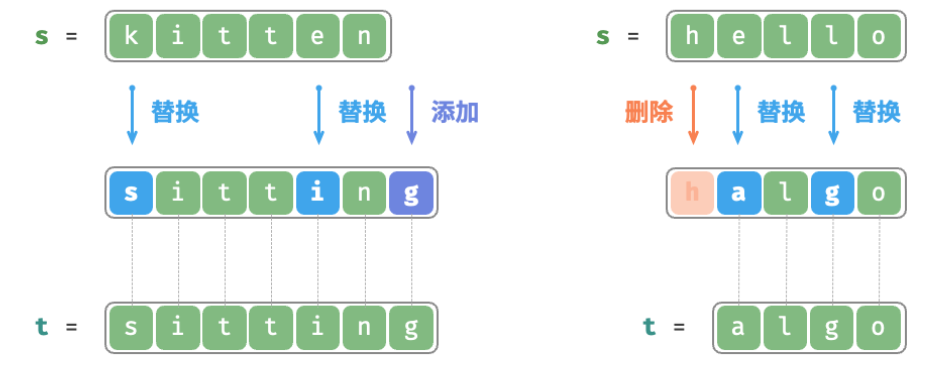
As shown in the figure below, kittenconverting to sittingrequires 3 editing steps, including 2 replacement operations and 1 adding operation; converting helloto algorequires 3 steps, including 2 replacing operations and 1 deletion operation.

The edit distance problem can be naturally explained by the decision tree model . A string corresponds to a tree node, and a decision round (an editing operation) corresponds to an edge of the tree.

As shown in the figure below, without restricting operations, each node can derive many edges, and each edge corresponds to an operation, which means that there are many possible paths from hellotransformation to .algo

From the perspective of a decision tree, the goal of this question is to find the shortest path between hellonodes algo.

Dynamic programming ideas

Step 1: Think about the decision-making in each round, define the state, and get $dp$ ​​table

The decision in each round is for the string $s$ to perform an editing operation.

We hope that during the editing operation, the size of the problem gradually shrinks so that sub-problems can be constructed. Let the string $s$ and$The\; lengths\; of\; t$ are respectively$n$ and$m$ , we first consider the characters s [ n − 1 ] s[n-1]at the end of the two strings$s[n-1]$ and$t[m-1]$ 。

• If $s[n-1]$ and$t[m-1]$ are the same, we can skip them and consider$s[n-2]$ and$t[m-2]$ 。
• If $s[n-1]$ and$t[m-1]$ different, we need to$s$ performs an edit (insertion, deletion, replacement) so that the characters at the end of the two strings are the same, so that they can be skipped and smaller problems can be considered.

That is, we have the string ssEach round of decision-making (editing operation) performed in$s$$s$ andttThe remaining characters to be matched in$t\; change.$Therefore, the status is currently in$s$ andttiithconsidered in$t$$i$ and$j$ characters, recorded as$[i,j]$ 。

state $[i,j]$ corresponding sub-problem:convert ssthe first iiof$s$$i$ characters changed to$t$ 's frontjjThe minimum number of editing steps required for$j$ characters .

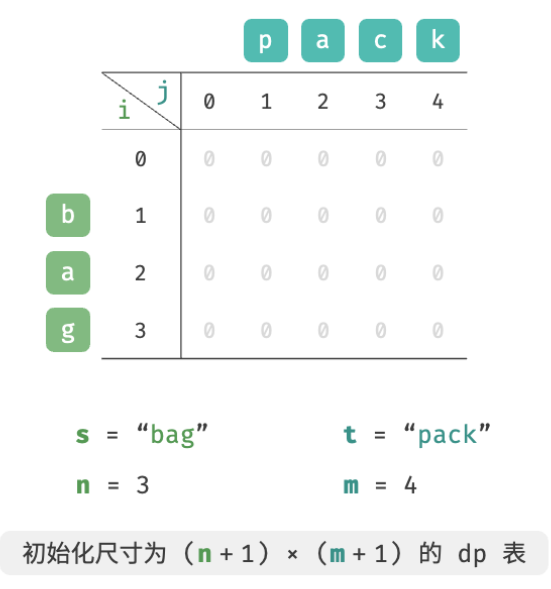
At this point, we get a size of $(i+1)\times (j+1)$ Two-dimensional$dp$ ​​table.

Step 2: Find the optimal substructure and derive the state transition equation

Consider the subproblem $dp[i,j]$ , the tail characters of the two corresponding strings are$s[i-1]$ and$t[j-1]$ , which can be divided into three situations as shown in the figure below according to different editing operations.

1. s $s[i-1]$ add t [ j − 1 ] t[j-1]after$t[j-1]$ , then the remaining subproblem$dp[i,j-1]$ 。
2. Delete $s[i-1]$ , then the remaining subproblem$dp[i-1,j]$ 。
3. General $s[i-1]$ is replaced by$t[j-1]$ , then the remaining subproblem$dp[i-1,j-1]$ 。

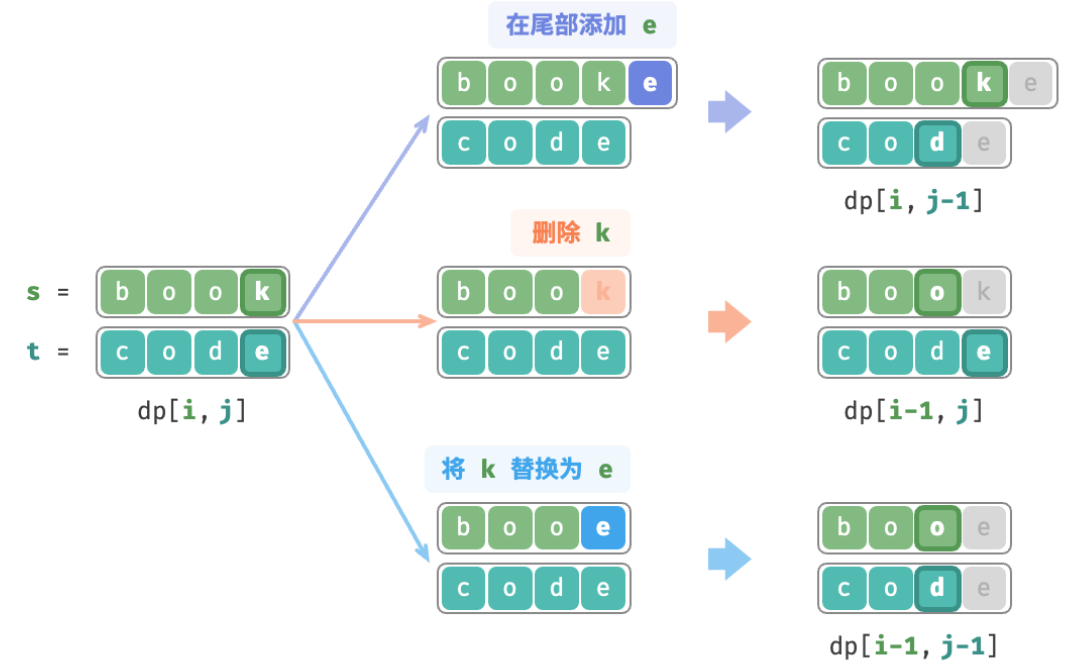
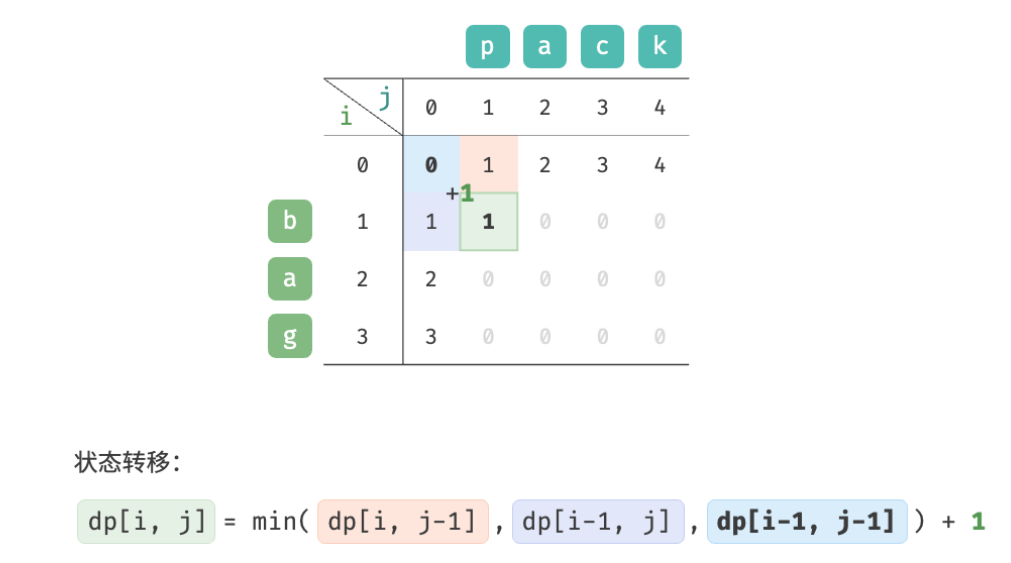
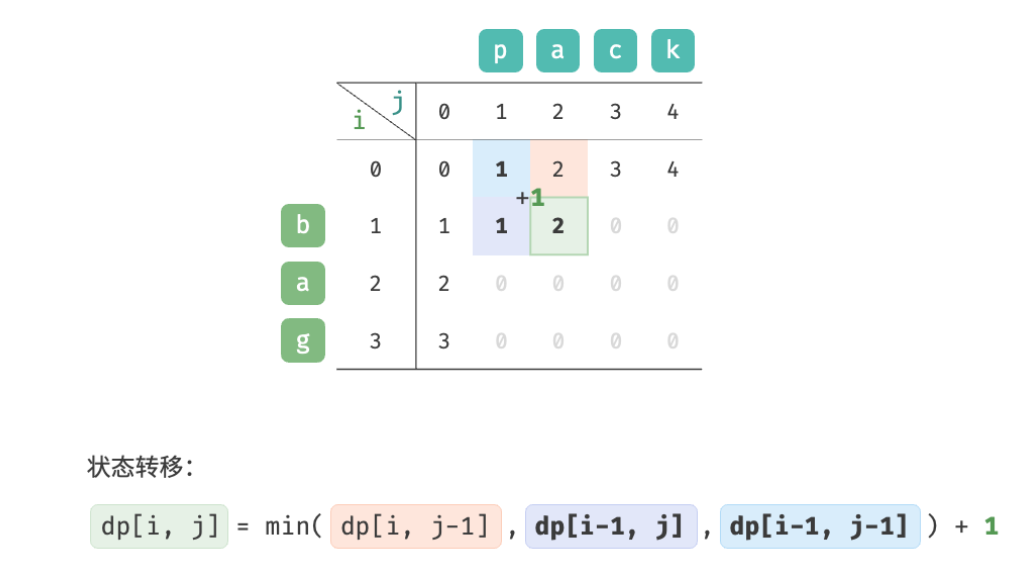
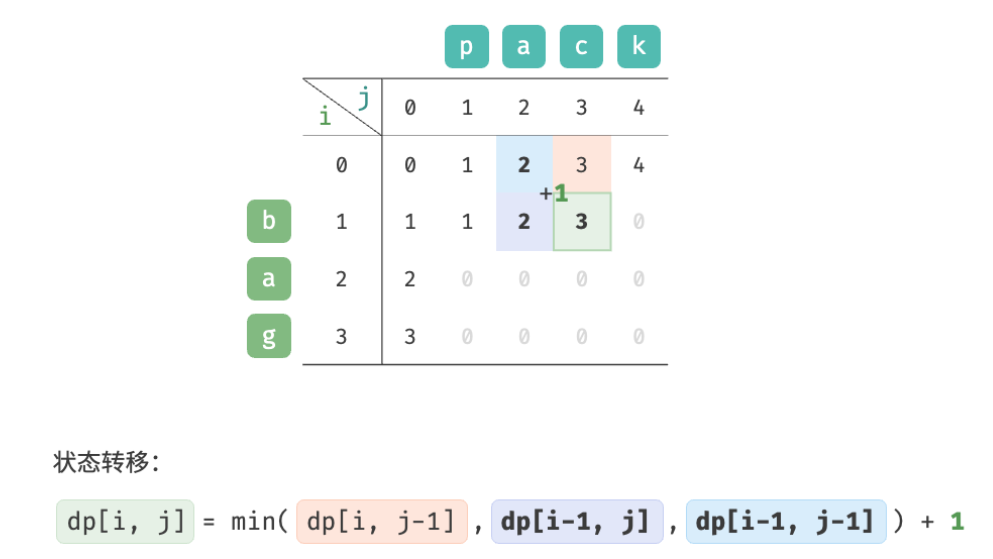
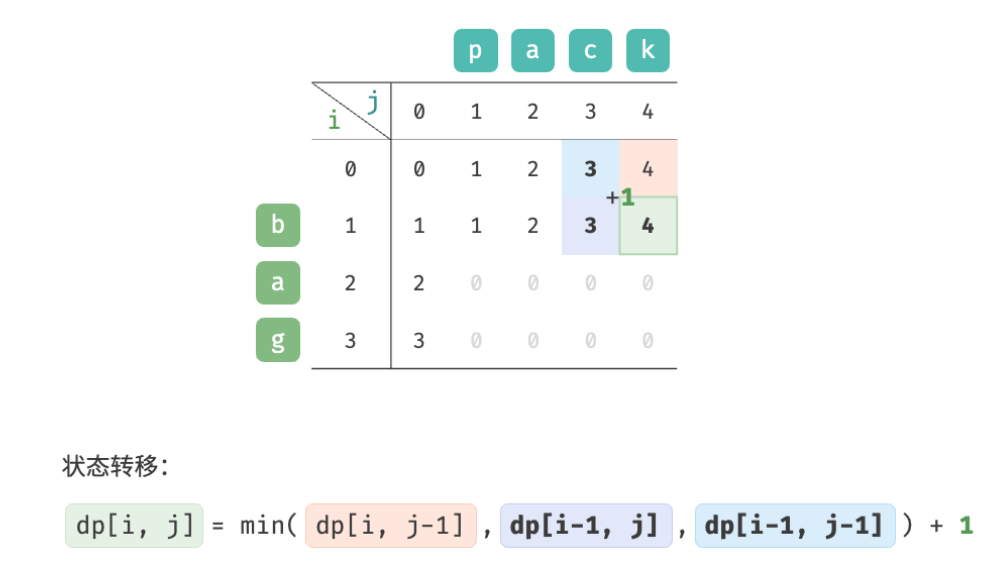
Based on the above analysis, the optimal substructure can be obtained: $dp[i,$The minimum number of editing steps for$j$$]$$dp[i,j-1]$、$dp[i-1,j]$、$dp[i-1,j-1]$ The minimum number of editing steps among the three, plus the number of editing steps this time$1$ . The corresponding state transition equation is:

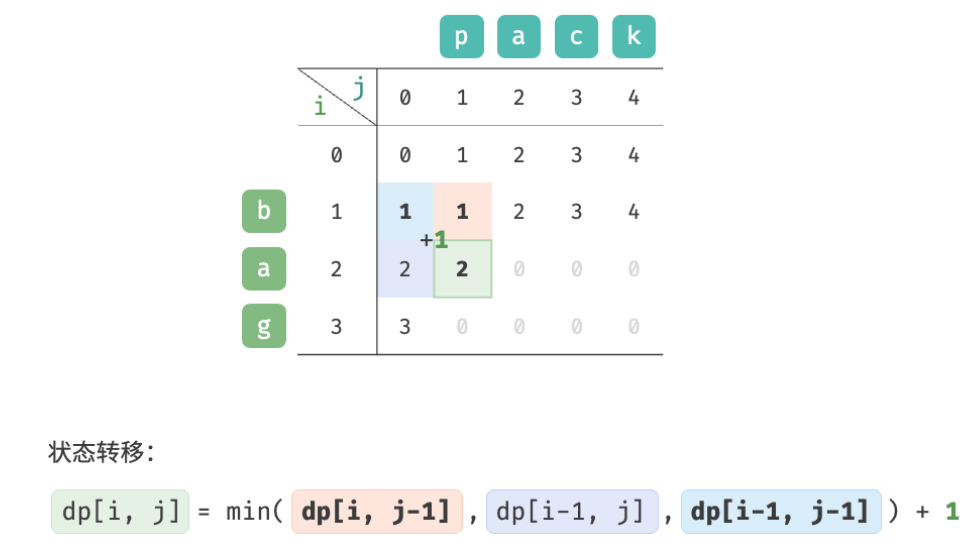
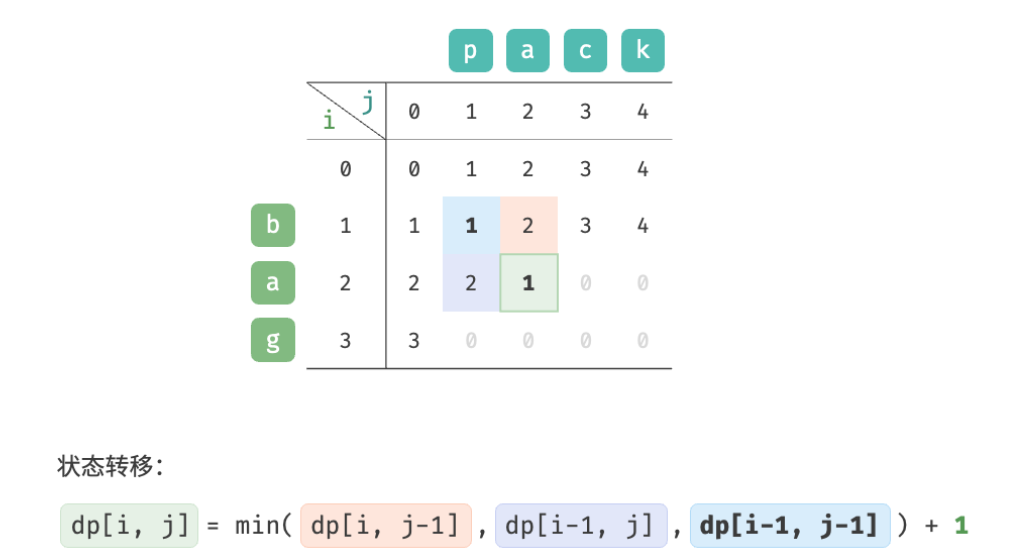
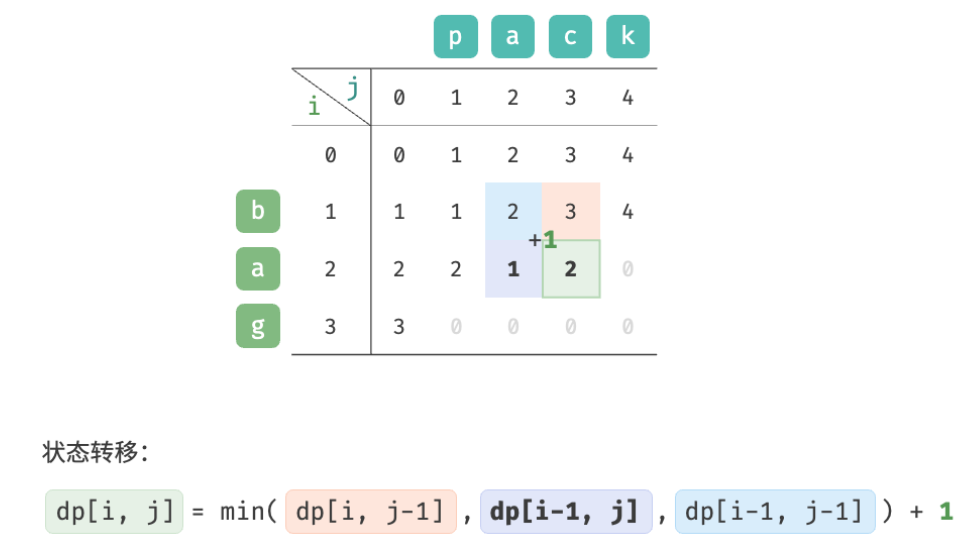
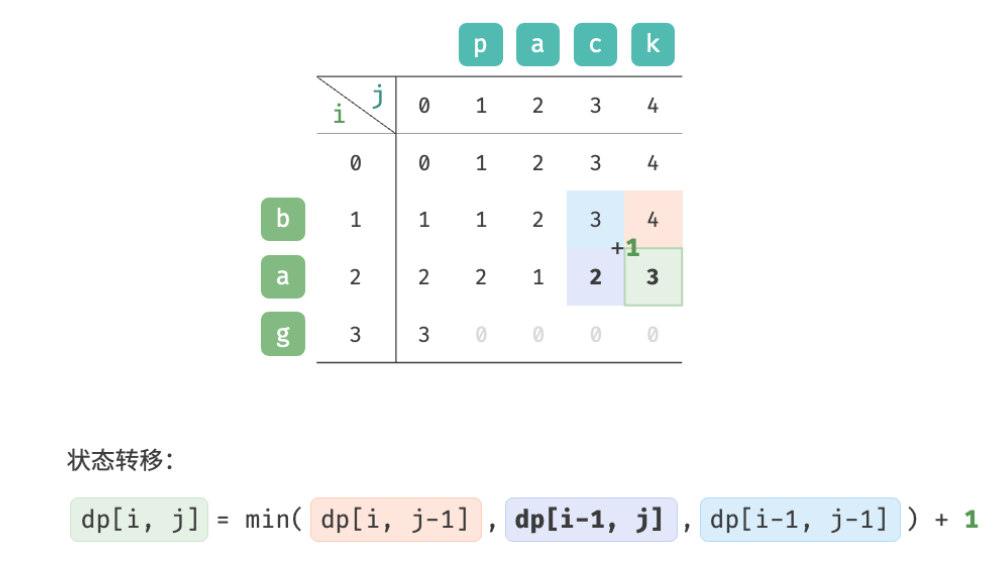
$$dp[i,j]=\min (dp[i,j-1],dp[i-1,j],dp[i-1,j-1])+1$$

Please note that when $s[i-1]$ and$t[j-1]$ are the same, there is no need to edit the current character. In this case, the state transition equation is:

$$dp[i,j]=dp[i-1,j-1]$$

Step 3: Determine boundary conditions and state transition sequence

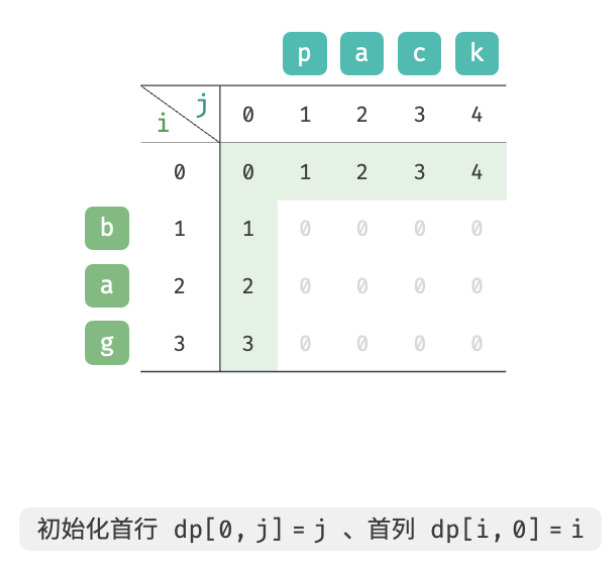
When both strings are empty, the number of editing steps is $0$ , that is,$dp[0,0]=0$ . When$s$ is empty but$When\; t$ is not empty, the minimum number of editing steps is equal to$The\; length\; of\; t$ , that is, the first row$dp[0,j]=j$ . When$s$ is not empty but$When\; t$ is empty, it is equal to$The\; length\; of\; s$ , that is, the first column$dp[i,0]=i$ 。

Observe the state transition equation and solve $dp[i,j]$ relies on the solutions on the left, above, and above left, so the entire$dp$ ​​table is enough.

Code

=== “Python”

```python title="edit_distance.py"
[class]{}-[func]{edit_distance_dp}
```

=== “C++”

```cpp title="edit_distance.cpp"
[class]{}-[func]{editDistanceDP}
```

=== “Java”

```java title="edit_distance.java"
[class]{edit_distance}-[func]{editDistanceDP}
```

=== “C#”

```csharp title="edit_distance.cs"
[class]{edit_distance}-[func]{editDistanceDP}
```

=== “Go”

```go title="edit_distance.go"
[class]{}-[func]{editDistanceDP}
```

=== “Swift”

```swift title="edit_distance.swift"
[class]{}-[func]{editDistanceDP}
```

=== “JS”

```javascript title="edit_distance.js"
[class]{}-[func]{editDistanceDP}
```

=== “TS”

```typescript title="edit_distance.ts"
[class]{}-[func]{editDistanceDP}
```

=== “Dart”

```dart title="edit_distance.dart"
[class]{}-[func]{editDistanceDP}
```

=== “Rust”

```rust title="edit_distance.rs"
[class]{}-[func]{edit_distance_dp}
```

=== “C”

```c title="edit_distance.c"
[class]{}-[func]{editDistanceDP}
```

=== “Zig”

```zig title="edit_distance.zig"
[class]{}-[func]{editDistanceDP}
```

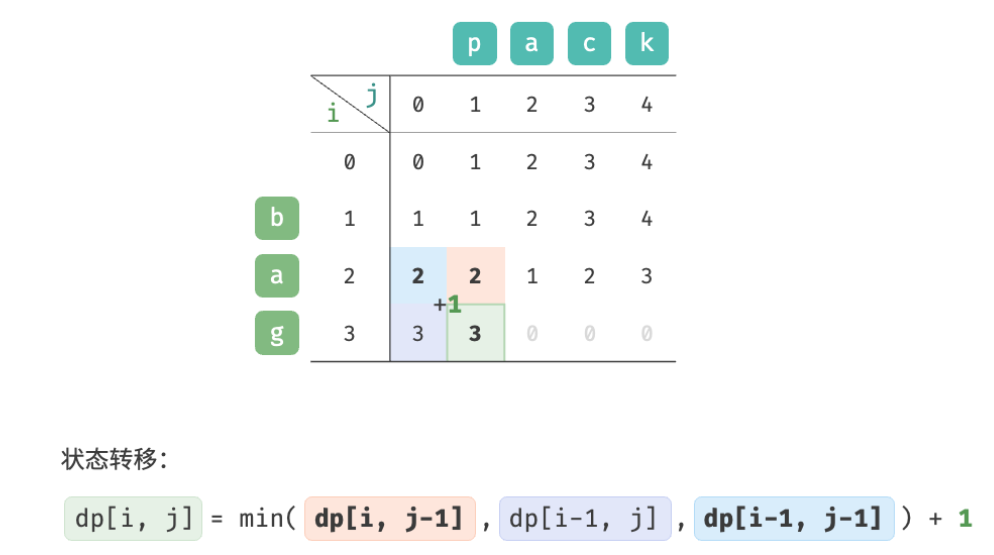
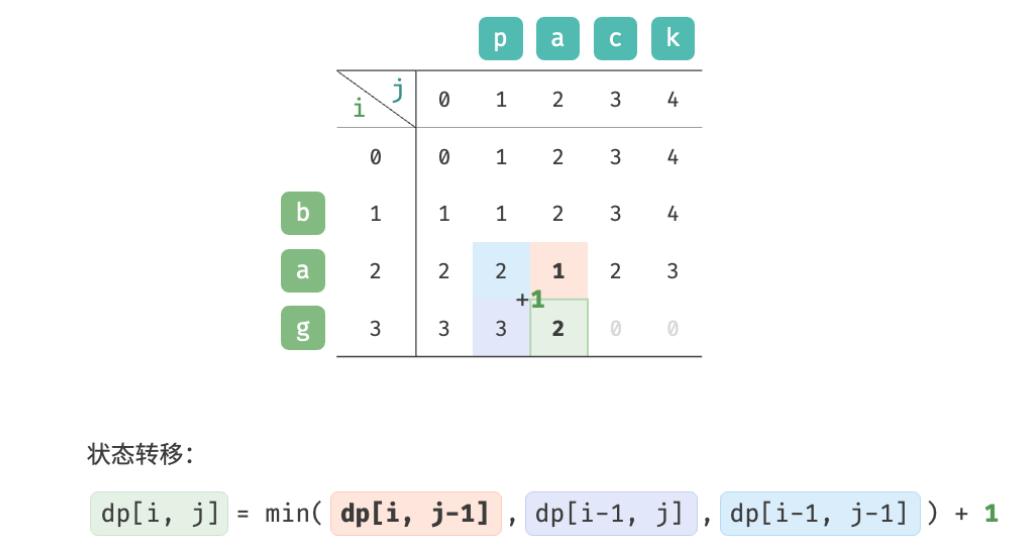
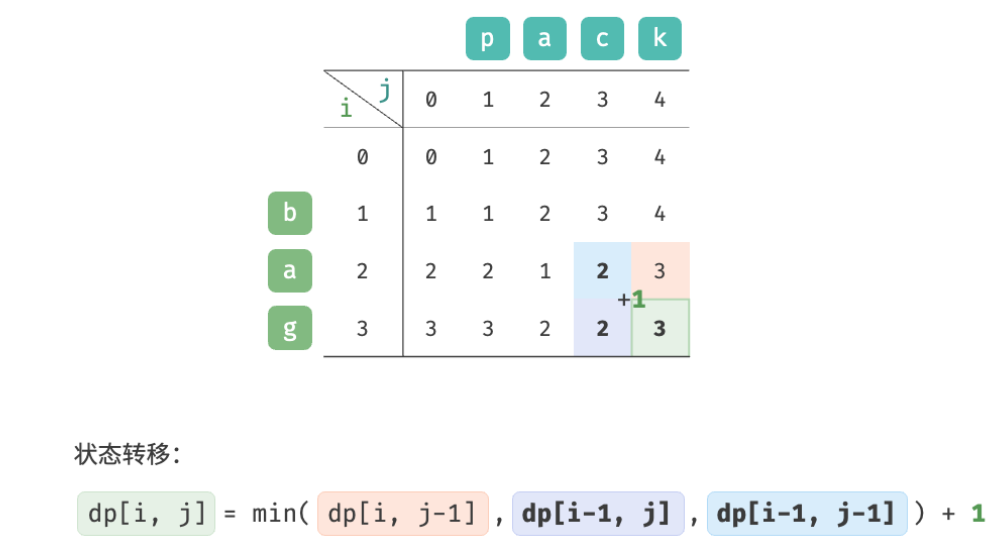
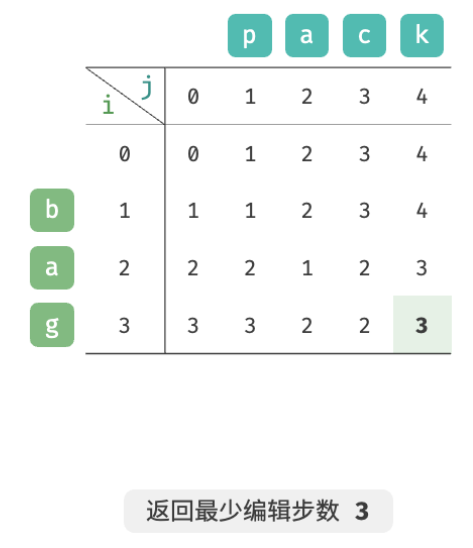
As shown in the figure below, the state transition process of the edit distance problem is very similar to the knapsack problem, and both can be regarded as the process of filling in a two-dimensional grid.

=== “<1>”

=== “<2>”

=== “<3>”

=== “<4>”

=== “<5>”

=== “<6>”

=== “<7>”

=== “<8>”

=== “<9>”

=== “<10>”

=== “<11>”

=== “<12>”

=== “<13>”

=== “<14>”

=== “<15>”

space optimization

Since $dp[i,j]$ is given by the upper$dp[i-1,j]$ , left$dp[i,j-1]$ , upper left state$dp[i-1,j-1]$ is transferred, and the forward order traversal will lose the upper left$dp[i-1,j-1]$ , reverse order traversal cannot construct$dp[i,j-1]$ , so both traversal orders are undesirable.

To do this, we can use a variable leftupto temporarily store the upper left solution $dp[i-1,j-1]$ , so only the left and upper solutions need to be considered. The situation at this time is the same as the complete knapsack problem, and forward order traversal can be used.

=== “Python”

```python title="edit_distance.py"
[class]{}-[func]{edit_distance_dp_comp}
```

=== “C++”

```cpp title="edit_distance.cpp"
[class]{}-[func]{editDistanceDPComp}
```

=== “Java”

```java title="edit_distance.java"
[class]{edit_distance}-[func]{editDistanceDPComp}
```

=== “C#”

```csharp title="edit_distance.cs"
[class]{edit_distance}-[func]{editDistanceDPComp}
```

=== “Go”

```go title="edit_distance.go"
[class]{}-[func]{editDistanceDPComp}
```

=== “Swift”

```swift title="edit_distance.swift"
[class]{}-[func]{editDistanceDPComp}
```

=== “JS”

```javascript title="edit_distance.js"
[class]{}-[func]{editDistanceDPComp}
```

=== “TS”

```typescript title="edit_distance.ts"
[class]{}-[func]{editDistanceDPComp}
```

=== “Dart”

```dart title="edit_distance.dart"
[class]{}-[func]{editDistanceDPComp}
```

=== “Rust”

```rust title="edit_distance.rs"
[class]{}-[func]{edit_distance_dp_comp}
```

=== “C”

```c title="edit_distance.c"
[class]{}-[func]{editDistanceDPComp}
```

=== “Zig”

```zig title="edit_distance.zig"
[class]{}-[func]{editDistanceDPComp}
```