Article directory
Personal notes:
1: Unary Taylor expansion formula
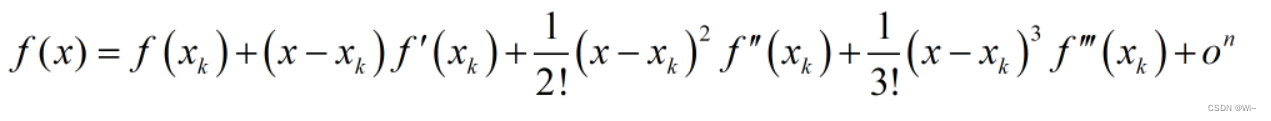 Example: f(x) = 3x² + 2x + 5 Taylor expansion at x=0 or x=1
Example: f(x) = 3x² + 2x + 5 Taylor expansion at x=0 or x=1
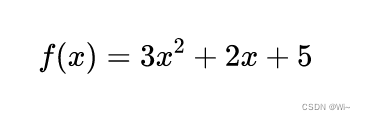
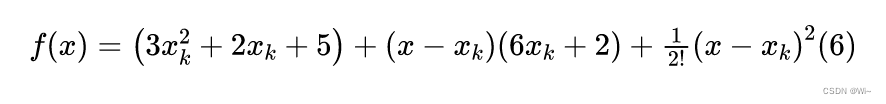 When x=0:
When x=0:
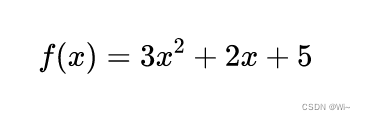
When x=1:
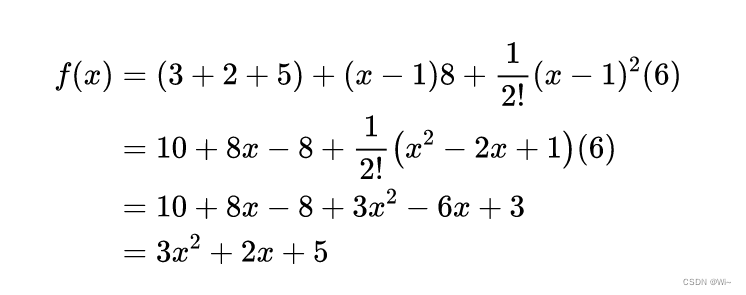
No matter how much Xk is equal to, the sum of the final expanded formulas is equal to f(x) = 3x² + 2x + 5
2: Binary Taylor expansion formula
Taylor expansion of x and y at k:
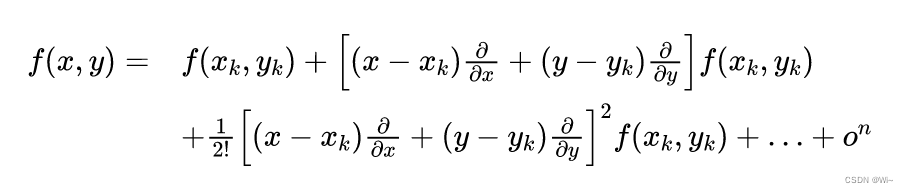
simplified:
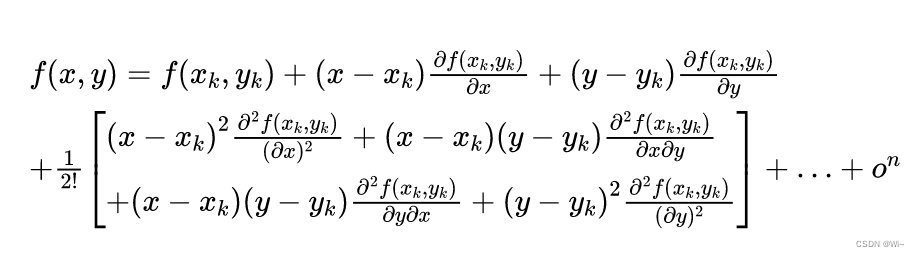
Simplification:
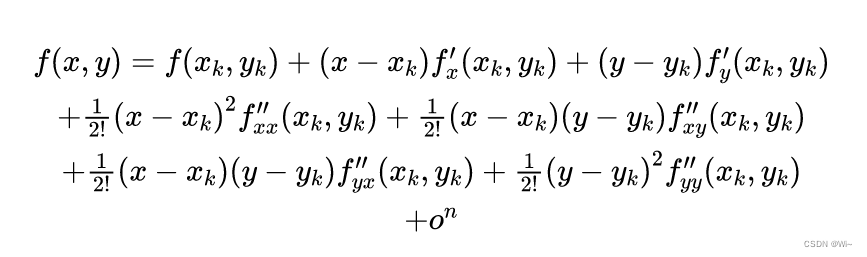 ①
①
fxx ′ ′ f''_{xx}fxx′′is taking two derivatives with respect to x.
②
f x y ′ ′ f''_{xy} fxy′′It is to take a derivative with respect to x first, and then take a derivative with respect to y.
③
f y x ′ ′ f''_{yx} fyx′′It is to take a derivative with respect to y first, and then take a derivative with respect to x.
(where ③ = ②)
④
f y y ′ ′ f''_{yy} fyy′′is taking the derivative of y twice.
3: Hessian matrix of binary functions
Binary function point f ( x 1 , x 2 ) f(x_1,x_2)f(x1,x2) atX ( k ) ( x 1 ( k ) , x 2 ( k ) ) X^{(k)}(x_1^{(k)},x_2^{(k)})X(k)(x1(k),x2(k)) at the Taylor expansion is:
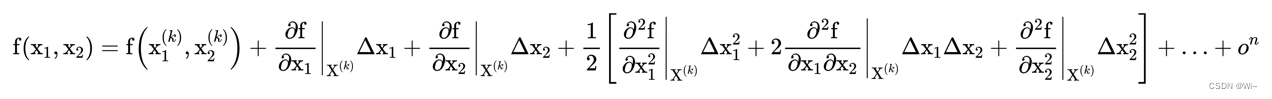
where Δ x 1 Δ x_1Δx _1 = x 1 x_1 x1 − x 1 ( k ) x_1^{(k)} x1(k), Δ x 2 Δ x_2Δx _2 = x 2 x_2 x2 − x 2 ( k ) x_2^{(k)} x2(k)
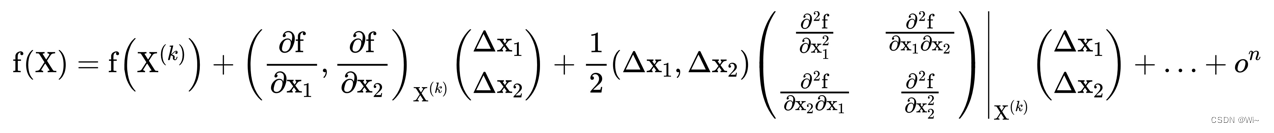
Right now:
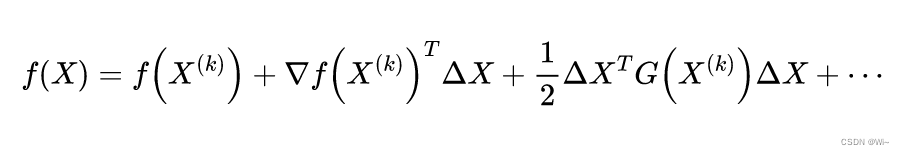
(1): where
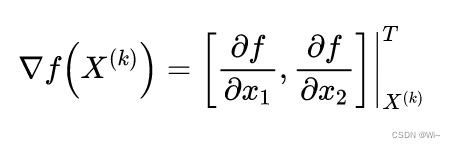
it is f ( X ) f(X)f ( X ) atX ( k ) X^{(k)}X( k ) Gradient at point.
(2): G ( X ( k ) ) G(X^{(k)}) G(X( k ) )isf ( x 1 , x 2 ) f(x_1,x_2)f(x1,x2) atX ( k ) X^{(k)}XHessian matrixat ( k ) . It is given by the functionf ( x 1 , x 2 ) f(x_1,x_2)f(x1,x2) atX ( k ) X^{(k)}XThe square matrix composed of the second order partial derivatives at ( k ) .
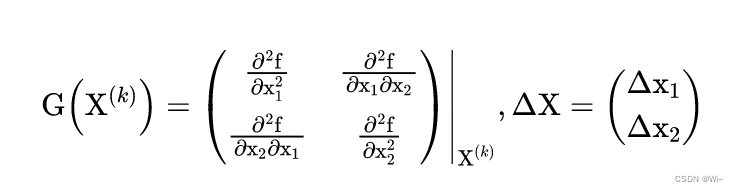
4: Hessian matrix of multivariate functions
1: Multivariate function f ( x 1 , x 2 , . . . , xn ) f(x_1,x_2,...,x_n)f(x1,x2,...,xn) at pointx ( k ) x^{(k)}xThe Taylor expansion at ( k )
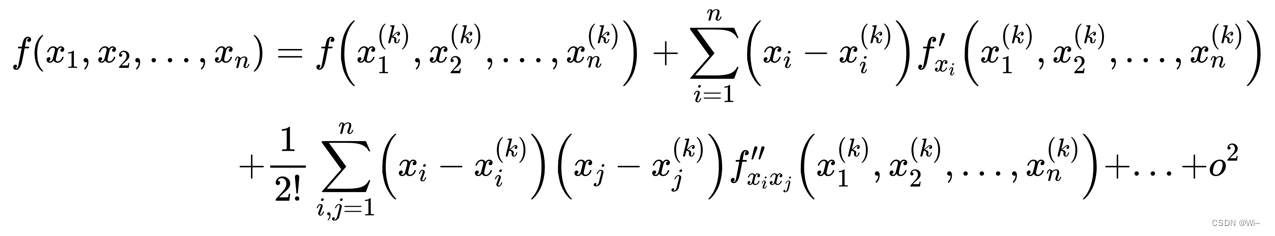 is: Write the Taylor (Taylor) expansion in the form of a matrix:
is: Write the Taylor (Taylor) expansion in the form of a matrix:
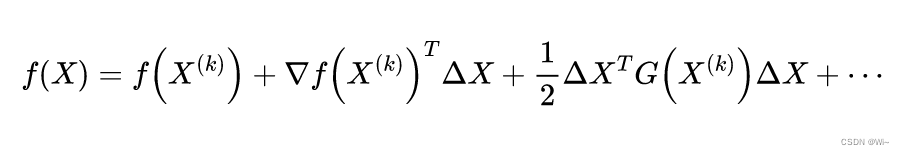 where:
where:
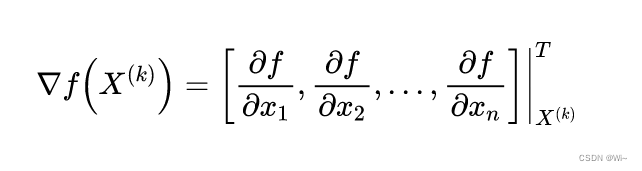
it isf ( X ) f(X)f ( X ) atX ( k ) X^{(k)}X( k ) Gradient at point.
(2):G ( X ( k ) ) G(X^{(k)})G(X( k ) )isf ( x 1 , x 2 , . . . , xn ) f(x_1,x_2,...,x_n)f(x1,x2,...,xn) atX ( k ) X^{(k)}XHessian matrixat ( k ) . It is given by the functionf ( x 1 , x 2 , . . . , xn ) f(x_1,x_2,...,x_n)f(x1,x2,...,xn) atX ( k ) X^{(k)}X( k ) composed of second order partial derivativesn ∗ nn*nn∗n order square matrix.
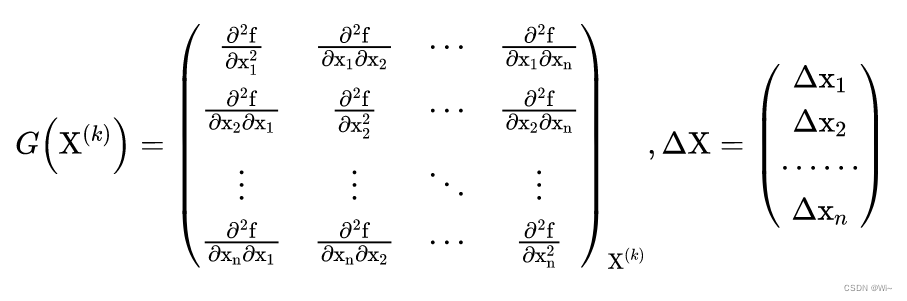 2:
2:

 For example:
For example:

5: Jacobian matrix of multivariate functions (Jacobian matrix)
1. Overview
Suppose fff: R n R^n Rn → R m R^m Rm is a function whose input is a vectorx ∈ R nx ∈ R^nx∈Rn , the output is the vectory = f ( x ) ∈ R my = f(x)∈ R^my=f(x)∈Rm , andm ≥ nm ≥ nm≥n is a European stylennConvert n- dimensional space to EuclideanmmThe function of m- dimensional space, this function is determined bymmComposed of m real functions:f 1 ( x 1 , … , xn ) f_1(x_1,…,x_n)f1(x1,…,xn),…, f m ( x 1 , … , x n ) f_m(x_1,…,x_n) fm(x1,…,xn) The partial derivatives of these functions (if they exist) can be composed into am∗nm∗nThe matrix of m ∗ n , this is the so-called Jacobian matrix:
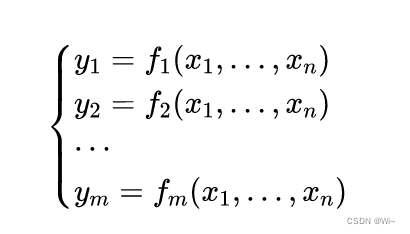
Then the Jacobian matrix is an m × nm × nm×n matrix, usually defined as
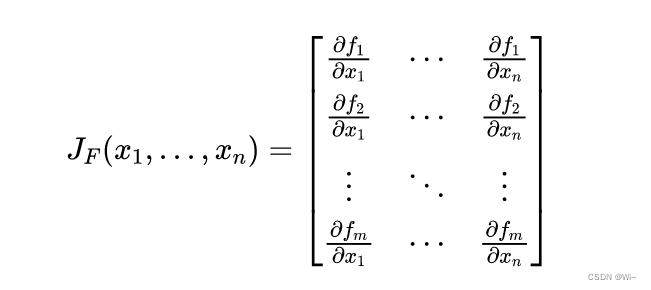
2: Example
Let’s look at an actual data fitting process, input:
independent variable: x = x =x={ 1 , 2 , 4 , 5 , 8 1,2,4,5,8 1,2,4,5,8 }
Dependent variable:y = y =y={ 3.2939 , 4.2699 , 7.1749 , 9.3008 , 20.259 3.2939,4.2699,7.1749,9.3008,20.259 3.2939,4.2699,7.1749,9.3008,20.259 }
Goal: Use the function f = p 1 ∗ ep 2 ∗ x − yf=p_1 ∗ e^{p_2∗x}−yf=p1∗ep2∗ x −yfor fitting, where the independent variablexxx , dependent variableyyy , parameterp 1 p_1p1and p 2 p_2p2, for parameter p 1 p_1p1and p 2 p_2p2Take the derivative:
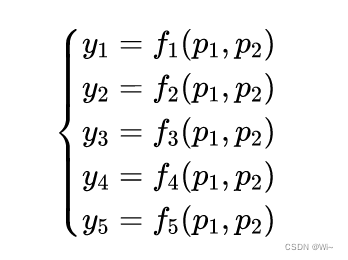
ep ∗ xe^{p*x}ep ∗ x versusppp is derived:x ∗ ep ∗ xx*e^{p*x}x∗ep∗x
Jacobian matrix description:
Jacobian矩阵 =
[ exp(p2), p1*exp(p2)]
[ exp(2*p2), 2*p1*exp(2*p2)]
[ exp(4*p2), 4*p1*exp(4*p2)]
[ exp(5*p2), 5*p1*exp(5*p2)]
[ exp(8*p2), 8*p1*exp(8*p2)]
Right now:
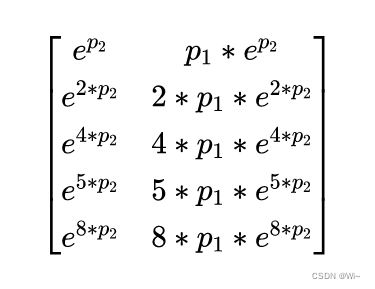
references
Jacobian Matrix 2
Jacobian Matrix Intuitive Image Understanding