Hungarian Algorithm Learning Record

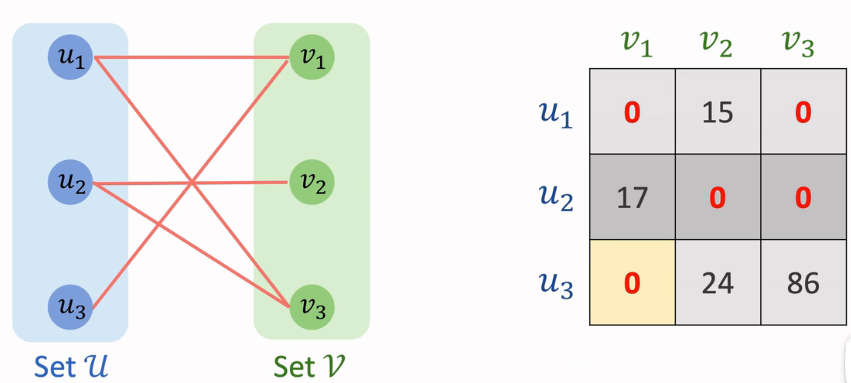
The Hungarian algorithm is mainly used to solve two problems: finding the maximum number of matches and the minimum number of points covered in a bipartite graph.
The Hungarian algorithm actually has two algorithms, which respectively solve the assignment problem and the bipartite graph maximum matching problem. Here, the algorithm refers to the Hungarian algorithm for solving the assignment problem.

processing flow

method one

How to achieve it?

Code

rank reduction

This function is mainly executed. In this function, row reduction and column reduction operations are performed. At the same time, cover_zeros.calculate() is used for trial assignment to obtain the row and column where the independent 0 element is located.

def calculate(self):
    """
    实施匈牙利算法的函数
    """
    result_matrix = self._cost_matrix.copy()

    # 步骤 1: 矩阵每一行减去本行的最小值
    for index, row in enumerate(result_matrix):
        result_matrix[index] -= row.min()

    # 步骤 2: 矩阵每一列减去本行的最小值
    for index, column in enumerate(result_matrix.T):
        result_matrix[:, index] -= column.min()
    # print('步骤2结果 ',result_matrix)
    # 步骤 3： 使用最少数量的划线覆盖矩阵中所有的0元素
    # 如果划线总数不等于矩阵的维度需要进行矩阵调整并重复循环此步骤
    total_covered = 0
    while total_covered < self._size:
        time.sleep(1)
        # print("---------------------------------------")
        # print('total_covered: ',total_covered)
        # print('result_matrix:',result_matrix)
        # 使用最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量
        cover_zeros = CoverZeros(result_matrix)
        single_zero_pos_list = cover_zeros.calculate()
        covered_rows = cover_zeros.get_covered_rows()
        covered_columns = cover_zeros.get_covered_columns()
        total_covered = len(covered_rows) + len(covered_columns)

        # 如果划线总数不等于矩阵的维度需要进行矩阵调整（需要使用未覆盖处的最小元素）
        if total_covered < self._size:
            result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns)
    # 元组形式结果对存放到列表
    self._results = single_zero_pos_list
    # 计算总期望结果
    value = 0
    for row, column in single_zero_pos_list:
        value += self._input_matrix[row, column]
    self._totalPotential = value

Tick ​​and line and trial assignment

The completion of the trial assignment operation is mainly to complete the ticking and marking operation. It actually completes the operation of step 2 in the principle, but its code implementation is implemented according to the following process.

Method 2 (exactly the same as Method 1)

In fact, the effect of executing the above steps is exactly the same as that of step 2 at the beginning of the article. As shown below:

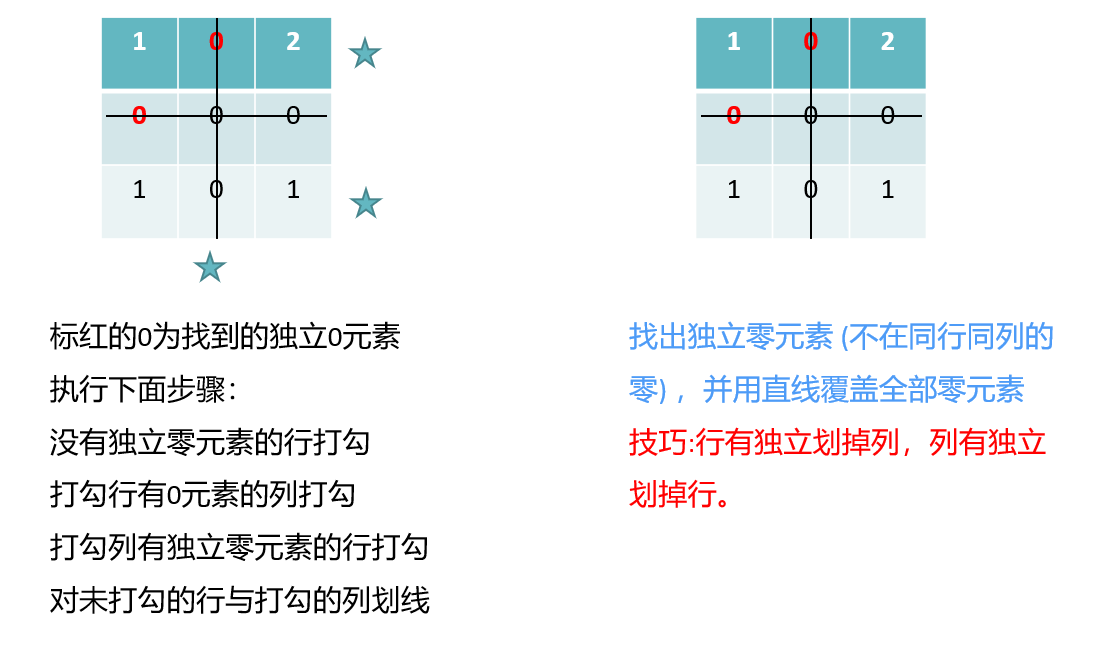
At the same time, the reason for subtracting the minimum value without crossing is to increase the number of 0 elements, and the addition of the minimum value of the cross line is actually an elementary column transformation to prevent negative values ​​from appearing.
In fact, it is more intuitive to understand step 3 according to the second method: subtract the minimum value from the unlined row, and add the minimum value to the lined column.

def calculate(self):
    '''进行计算'''
    # 储存勾选的行和列
    ticked_row = []
    ticked_col = []
    marked_zeros = []
    # 1、试指派并标记独立零元素
    while True:
        # print('_zero_locations_copy',self._zero_locations_copy)
        # 循环直到所有零元素被处理（_zero_locations中没有true）
        if True not in self._zero_locations_copy:
            break
        self.row_scan(marked_zeros)

    # 2、无被标记0（独立零元素）的行打勾
    independent_zero_row_list = [pos[0] for pos in marked_zeros]
    ticked_row = list(set(range(self._shape[0])) - set(independent_zero_row_list))#的到未标记行
    # 重复3,4直到不能再打勾
    TICK_FLAG = True
    while TICK_FLAG:
        # print('ticked_row:',ticked_row,'   ticked_col:',ticked_col)
        TICK_FLAG = False
        # 3、对打勾的行中所含0元素的列打勾
        for row in ticked_row:
            # 找到此行
            row_array = self._zero_locations[row, :]
            # 找到此行中0元素的索引位置
            for i in range(len(row_array)):
                if row_array[i] == True and i not in ticked_col:
                    ticked_col.append(i)
                    TICK_FLAG = True

        # 4、对打勾的列中所含独立0元素的行打勾
        for row, col in marked_zeros:
            if col in ticked_col and row not in ticked_row:
                ticked_row.append(row)
                FLAG = True
    # 对打勾的列和没有打勾的行画画线
    self._covered_rows = list(set(range(self._shape[0])) - set(ticked_row))
    self._covered_columns = ticked_col

    return marked_zeros

There is a row_scan method inside this method, which is to scan the row line by line, and select independent zero elements, and marked_zeros is the selected 0 element.

 def row_scan(self, marked_zeros):
        '''扫描矩阵每一行，找到含0元素最少的行，对任意0元素标记（独立零元素），划去标记0元素（独立零元素）所在行和列存在的0元素'''
        min_row_zero_nums = [9999999, -1]
        for index, row in enumerate(self._zero_locations_copy):  # index为行号 找出改行最少的0元素
            row_zero_nums = collections.Counter(row)[True]
            if row_zero_nums < min_row_zero_nums[0] and row_zero_nums != 0:
                # 找最少0元素的行
                min_row_zero_nums = [row_zero_nums, index]#记录0的个数，哪行。
        # 最少0元素的行  min_row_zero_nums  记录0的个数，哪行
        row_min = self._zero_locations_copy[min_row_zero_nums[1], :]
        # 找到此行中任意一个0元素的索引位置即可
        row_indices, = np.where(row_min)#如两个0元素，分别为0，2，则返回前面的0即可。
        # 标记该0元素
        # print('row_min',row_min)
        marked_zeros.append((min_row_zero_nums[1], row_indices[0]))
        # 划去该0元素所在行和列存在的0元素
        # 因为被覆盖，所以把二值矩阵_zero_locations中相应的行列全部置为false，先将列变为false，再将行变为false
        self._zero_locations_copy[:, row_indices[0]] = np.array([False for _ in range(self._shape[0])])
        self._zero_locations_copy[min_row_zero_nums[1], :] = np.array([False for _ in range(self._shape[0])])

matrix adjustment

The last is the matrix adjustment after the failed trial assignment

def _adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):
    """计算未被覆盖元素中的最小值（m）,未被覆盖元素减去最小值m,行列划线交叉处加上最小值m"""
    adjusted_matrix = result_matrix
    # 计算未被覆盖元素中的最小值（m）
    elements = []
    for row_index, row in enumerate(result_matrix):
        if row_index not in covered_rows:
            for index, element in enumerate(row):
                if index not in covered_columns:
                    elements.append(element)
    min_uncovered_num = min(elements)
    # print('min_uncovered_num:',min_uncovered_num)
    # 未被覆盖元素减去最小值m
    for row_index, row in enumerate(result_matrix):
        if row_index not in covered_rows:
            for index, element in enumerate(row):
                if index not in covered_columns:
                    adjusted_matrix[row_index, index] -= min_uncovered_num
    # print('未被覆盖元素减去最小值m',adjusted_matrix)

    # 行列划线交叉处加上最小值m
    for row_ in covered_rows:
        for col_ in covered_columns:
            # print((row_,col_))
            adjusted_matrix[row_, col_] += min_uncovered_num
    # print('行列划线交叉处加上最小值m',adjusted_matrix)
    return adjusted_matrix

maximum matching edge

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i)
{
    
    
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]) //有边且未访问
        {
    
    
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
    
    
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int Hungarian()
{
    
    
    int cnt = 0;
    for (int i = 1; i <= M; ++i)
    {
    
    
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}

Replenish

In fact, the assignment problem above is actually a bipartite graph matching problem with minimum weight

After conversion: Is it familiar? Isn't this a bipartite graph matching problem? Here it is converted into a maximum match, and the maximum match here is also a complete match.