Data Structure and Algorithm Nine Tree Advanced

a balanced tree

We have studied binary search trees before and found that its query efficiency is much higher than that of simple linked lists and arrays. In most cases, this is indeed the case, but unfortunately, in the worst case, binary Lookup tree performance is still terrible.

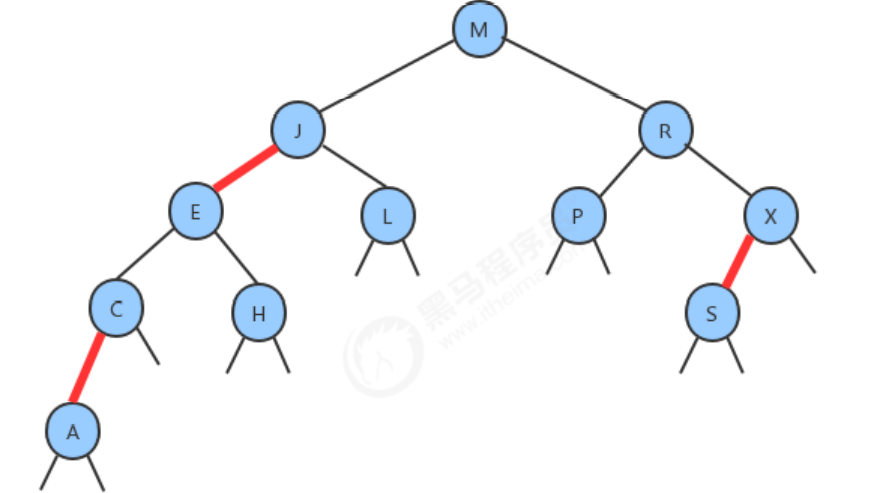
For example, we insert 9 data of 9, 8, 7, 6, 5, 4, 3, 2, 1 into the binary search tree in turn, then the final constructed tree looks like this:

We will find that if we want to find the element 1, the search efficiency will still be very low. The reason for the inefficiency is that the tree is unbalanced and all branches to the left. If we have a method that can make the generated tree look like a complete binary tree without being affected by the inserted data, then even in the worst case, the search The efficiency will still be very good.

1.1 2-3 search tree

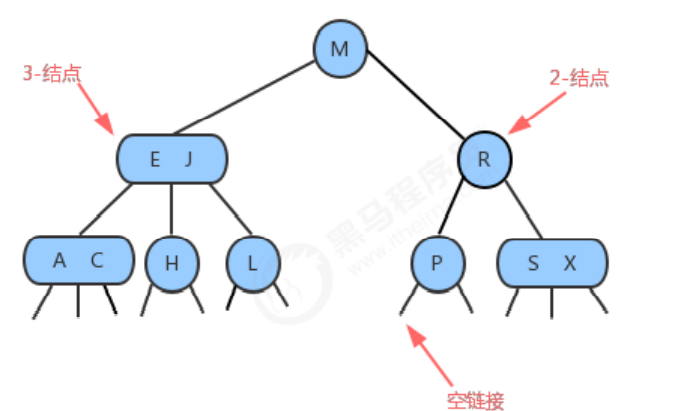
In order to keep the search tree balanced, we need some flexibility, so here we allow a node in the tree to hold multiple keys. To be precise, we call a node in a standard binary search tree 2-结点(contains one key and two chains), and now we introduce 3-结点that it contains two keys and three chains. 2-结点Each 3-结点chain in the sum corresponds to an interval generated by splitting the keys stored in it.

1.1.1 2-3 Definition of search tree

A 2-3 search tree is either empty or satisfies the following two requirements:

• 2-node:
  Contains a key (and its corresponding value) and two chains, the keys in the 2-3 tree pointed to by the left link are all smaller than the node, and the keys in the 2-3 tree pointed to by the right link are greater than the Node.
• 3-node:
  Contains two keys (and their corresponding values) and three chains, the keys in the 2-3 tree pointed to by the left link are all smaller than the node, and the keys in the 2-3 tree pointed to by the middle link are located in Between the two keys of the node, the keys in the 2-3 tree pointed to by the right link are all larger than the node.

1.1.2 Search

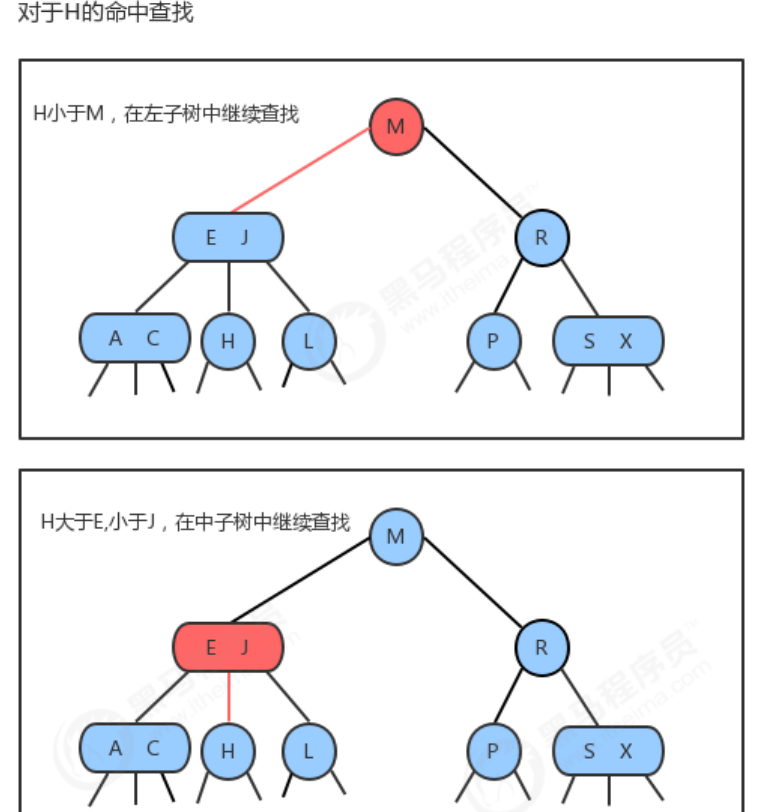
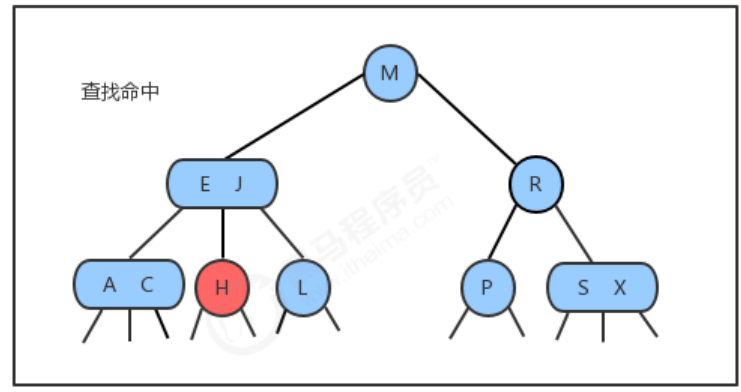
By generalizing the search algorithm of the binary search tree, we can directly obtain the search algorithm of the 2-3 tree. To determine if a key is in the tree, we first compare it to the key in the root node. If it is equal to any one of them, the search hits; otherwise, we find the connection pointing to the corresponding interval according to the comparison result, and continue searching recursively in the subtree it points to. If this is an empty link, the lookup misses.

1.1.3 Insertion

1.1.3.1 Insert a new key into the 2-node

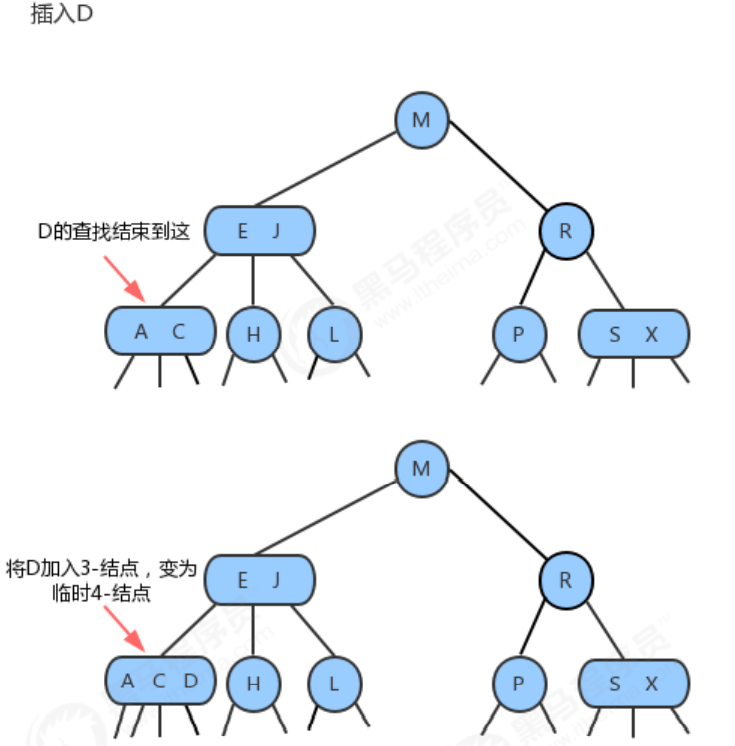
Inserting elements into the 2-3 tree is the same as inserting elements into the binary search tree. First, you need to search, and then hang the nodes to the unfound nodes. The reason why the 2-3 tree can guarantee the efficiency in the worst case is that it can still maintain a balanced state after insertion. If the node not found after the search is a 2-node, then it is easy, we just need to put the new element into this 2-node to make it a 3-node. But if the node you're looking for ends up in a 3-node, then it can be a bit tricky.

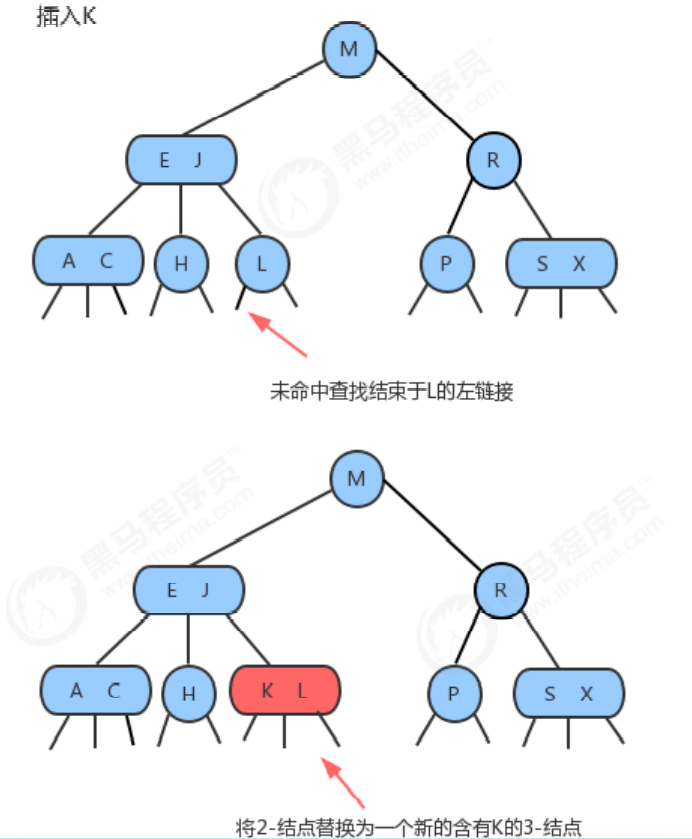
1.1.3.2 Inserting a new key into a tree containing only one 3-node

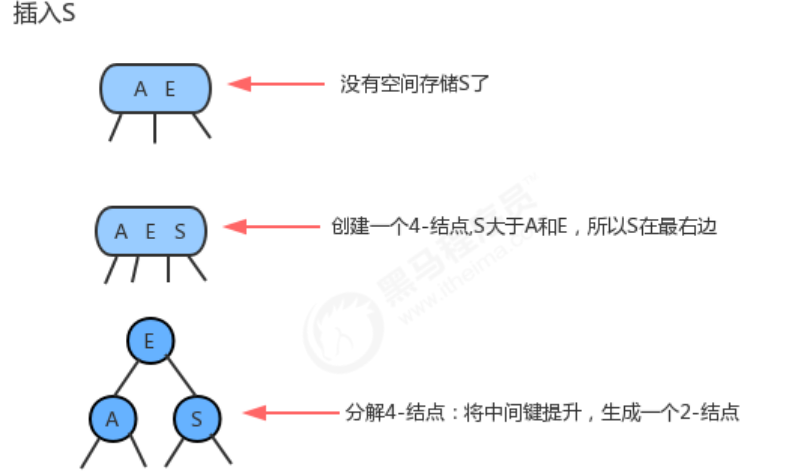
Assuming that the 2-3 tree contains only one 3-node, this node has two keys, and there is no room to insert the third key, the most natural way is to assume that this node can store three elements, temporarily make it becomes a 4-node, and it contains four links. We then promote the middle element of this 4-node with the left key as its left child and the right key as its right child. After the insertion is complete, it becomes a balanced 2-3 search tree, and the height of the tree changes from 0 to 1.

1.1.3.3 Insert a new key into a 3-node whose parent is a 2-node

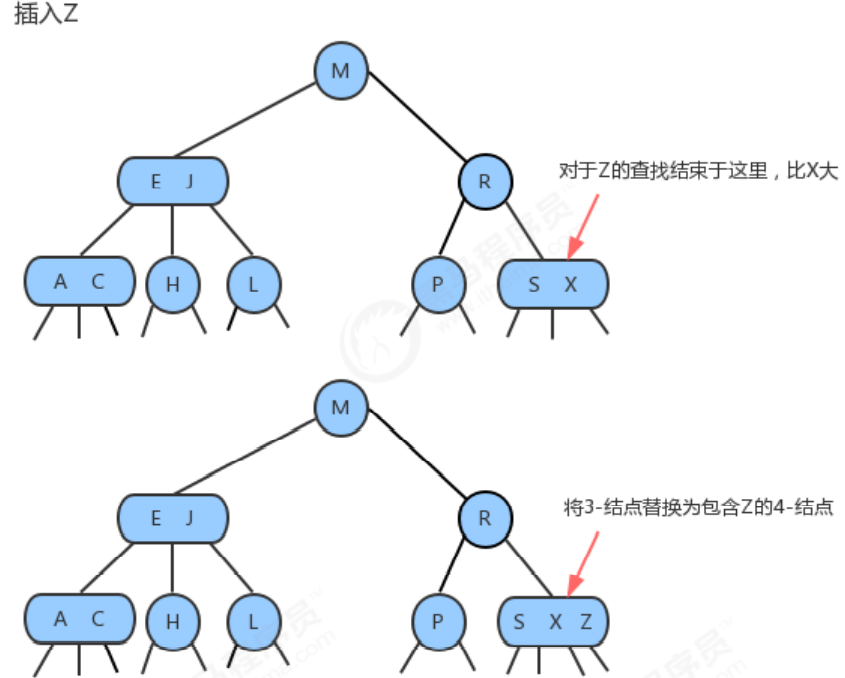
As in the above case, we can also insert new elements into the 3-node to make it a temporary 4-node, and then promote the middle element in the node to the parent node, which is 2 - In the node, make its parent node a 3-node, and then hang the left and right nodes at the appropriate positions of the 3-node.

1.3.1.4 Insert a new key into a 3-node whose parent is a 3-node

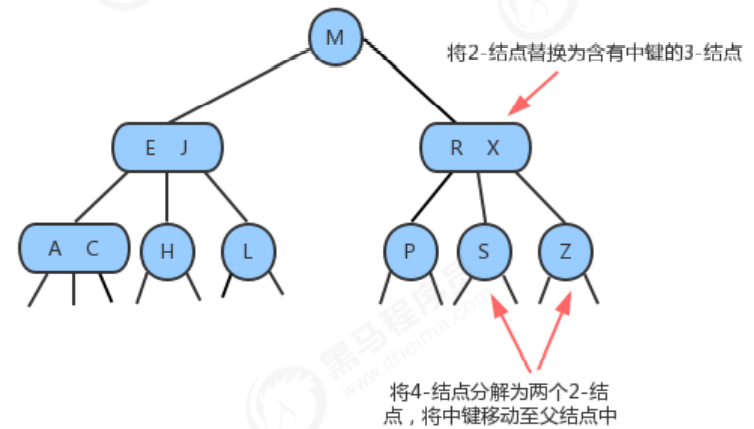
When the node we insert is a 3-node, we split the node and promote the middle element to the parent node, but at this time the parent node is a 3-node, after insertion, the parent node becomes Become a 4-node, and then continue to promote the middle element to its parent node, until a parent node is a 2-node, and then turn it into a 3-node, no need to continue to split.

1.3.1.5 Decomposing the root node

When the path from the inserted node to the root node is all 3-nodes, our root node will eventually program a temporary 4-node. At this time, we need to split the root node into two 2-node, add 1 to the height of the tree.

1.3.4 Properties of 2-3 trees

Through the analysis of the insertion operation of the 2-3 tree, we found that when inserting, the 2-3 tree needs to do some local transformations to maintain the balance of the 2-3 tree.

A perfectly balanced 2-3 tree has the following properties:

1. The path lengths of any empty link to the root node are equal.
2. When a 4-node is transformed into a 3-node, the height of the tree will not change, only when the root node is a temporary 4-node, when the root node is decomposed, the tree height will be +1.
3. The biggest difference between the 2-3 tree and the ordinary binary search tree is that the ordinary binary search tree grows from the top down, while the 2-3 tree grows from the bottom up.

1.3.5 Implementation of 2-3 tree

Implementing a 2-3 tree directly is more complicated because:

• Need to deal with different node types, which is very cumbersome;
• Multiple comparison operations are required to move the node down;
• Need to move up to split the 4-node;
• There are many situations for splitting 4-nodes;

2-3 The implementation of the search tree is more complicated, and in some cases, the balance operation after insertion may reduce the efficiency. But the 2-3 search tree, as a relatively important concept and idea, is very important for the red-black tree, B-tree and B+ tree that we will talk about later.

1.2 Red-black tree

We introduced the 2-3 tree earlier, and we can see that the 2-3 tree can ensure that the tree remains in a balanced state after inserting elements. In its worst case, all child nodes are 2-nodes, and the height of the tree is lgN, compared with our ordinary binary search tree, the height of the tree in the worst case is N, which does guarantee the time complexity in the worst case, but the 2-3 tree is too complicated to implement, so we introduce a A simple implementation of the 2-3 tree idea: red-black tree.

The red-black tree mainly encodes the 2-3 tree. The basic idea behind the red-black tree is to use a standard binary search tree (completely composed of 2-nodes) and some additional
information to represent 2-3 trees. We divide the links in the tree into two types:

Red link : Connect two 2-nodes to form a 3-node; Black link: It is a normal link in the 2-3 tree.

Specifically, we represent a 3-node as two 2-nodes connected by a left-sloping red link (two 2-nodes, one of which is the left child of the other). An advantage of this notation is that we can directly use the get method of the standard binary search tree without modification.

1.2.1 Definition of red-black tree

A red-black tree is a binary search tree that contains red-black links and satisfies the following conditions:

1. Red links are all left links;
2. No node is connected to two red links at the same time;
3. The tree is perfectly black balanced, that is, the number of black links on the path from any empty link to the root node is the same;

The following is the correspondence between the red-black tree and the 2-3 tree:

1.2.2 Red-black tree node API

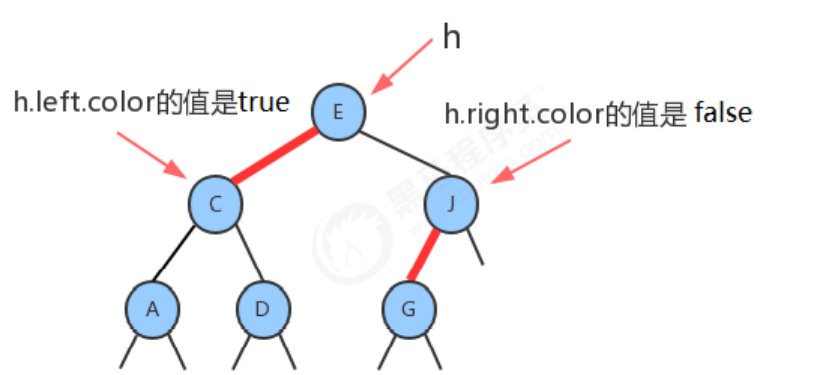
Because each node will only have one link pointing to itself (pointing to it from its parent node), we can add a Boolean variable color to the previous Node node to represent the color of the link. If the link pointing to it is red, then the value of the variable is true, if the link is black, then the value of the variable is false.

API Design:

Code

private class Node<Key,Value>{
    
    
	//存储键
	public Key key;
	//存储值
	private Value value;
	//记录左子结点
	public Node left;
	//记录右子结点
	public Node right;
	//由其父结点指向它的链接的颜色
	public boolean color;
	public Node(Key key, Value value, Node left,Node right,boolean color) {
    
    
		this.key = key;
		this.value = value;
		this.left = left;
		this.right = right;
		this.color = color;
	}
}

1.2.3 Balance

After some additions, deletions, modifications, and queries to the red-black tree, it is very likely that there will be a red right link or two consecutive red links, and these do not meet the definition of the red-black tree, so we need to rotate these cases Fix it so that the red-black tree remains balanced.

1.2.3.1 Left-handed

When the left child node of a node is black and the right child node is red, left rotation is required.
Premise: the current node is h, and its right child node is x;

Left-handed process:

1. Let the left child node of x become the right child node of h: h.right=x.left;
2. Let h be the left child of x: x.left=h;
3. Let the color attribute of h change to the color attribute value of x: x.color=h.color;
4. Let the color attribute of h become RED: h.color=true;

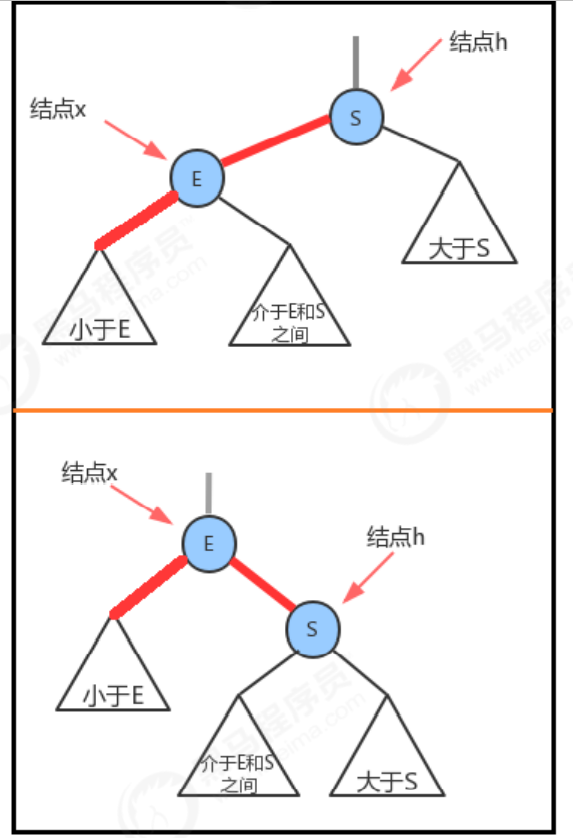
1.2.3.2 Right rotation

When the left child node of a certain node is red, and the left child node of the left child node is also red, right rotation is required.
Prerequisite: the current node is h, and its left child node is x;

Right rotation process:

1. Let the right child of x be the left child of h: h.left = x.right;
2. Let h be the right child of x: x.right=h;
3. Let the color of x change to the color attribute value of h: x.color = h.color;
4. Let the color of h be RED;

1.2.4 Inserting a new key into a single 2-node

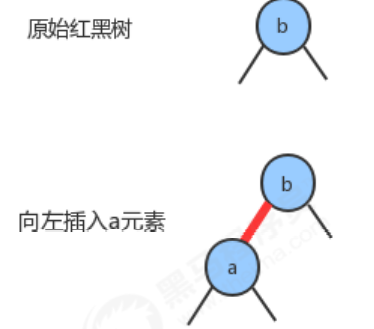
A red-black tree with only one key has only one 2-node. As soon as another key is inserted, we need to rotate them.

• If the new key is smaller than the key of the current node, we only need to add a red node, and the new red-black tree is completely equivalent to a single 3-node.

• If the new key is greater than the key of the current node, then the newly added red node will generate a red right link. At this time, we need to turn the red right link into a left link through left rotation, and the insertion operation is completed. The new red-black tree formed is still equivalent to a 3-node, which contains two keys and a red link.
  

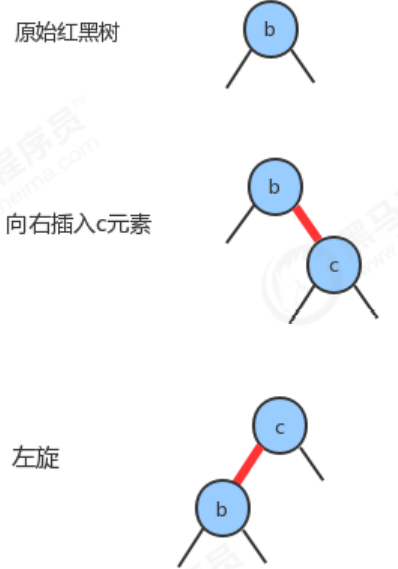
1.2.5 Insert a new key to the bottom 2-node

Inserting a new key into a red-black tree in the same way as a binary search tree will add a new node at the bottom of the tree (to ensure order), the only difference is that we will use the red link to The new node is connected to its parent node. If its parent is a 2-node, then the two approaches just discussed still apply.

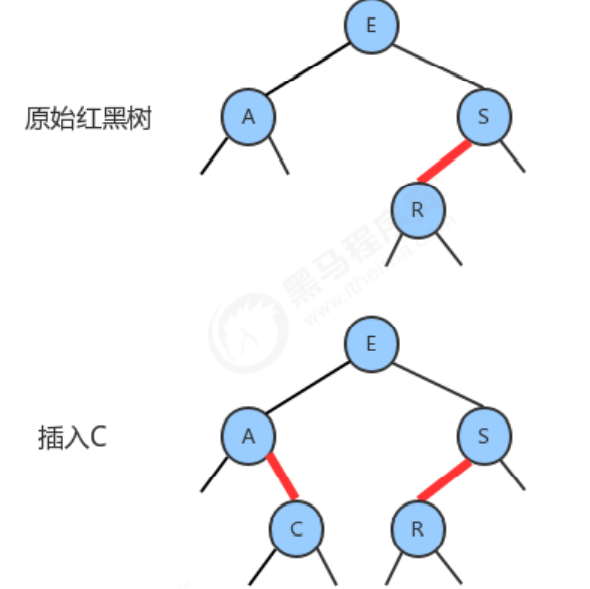
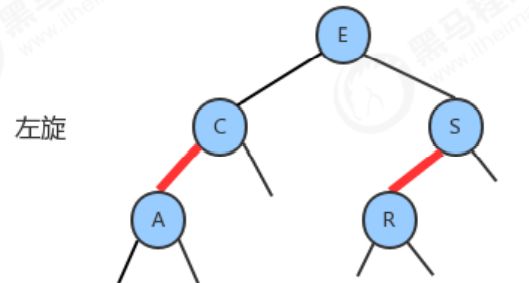
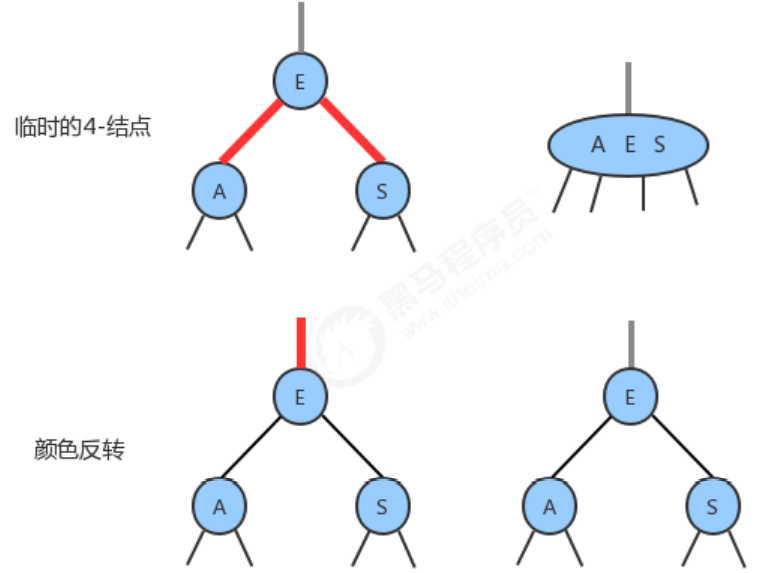
1.2.6 Color inversion

When the color of the left child node and the right child node of a node is RED, that is, a temporary 4-node appears. At this time, it is only necessary to change the color of the left child node and the right child node to BLACK, and change the color of the current node to RED at the same time.

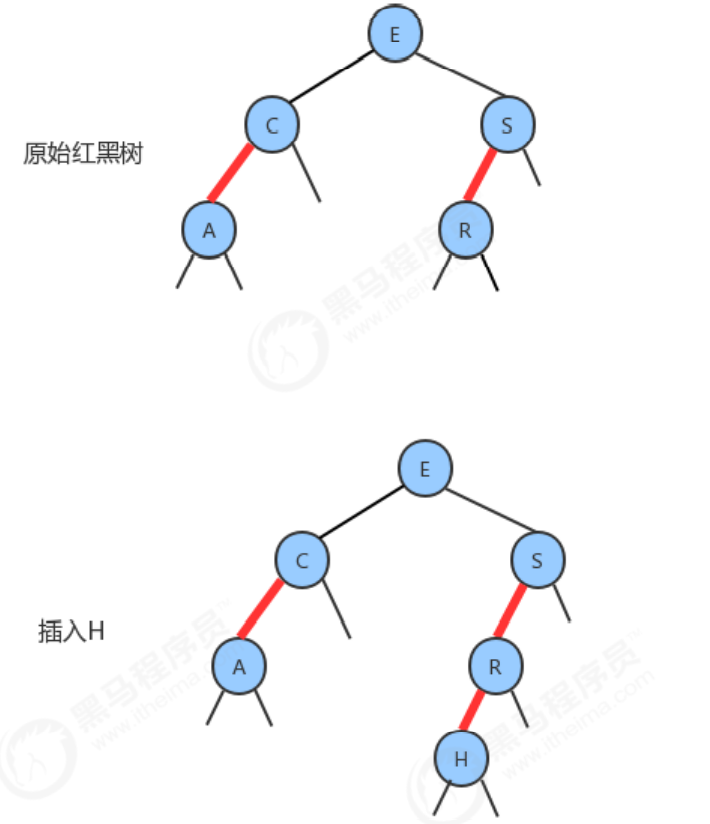
1.2.7 Insert a new key into a double key tree (ie a 3-node)

This situation can be divided into three sub-cases:

1. The new key is greater than both keys in the original tree
   
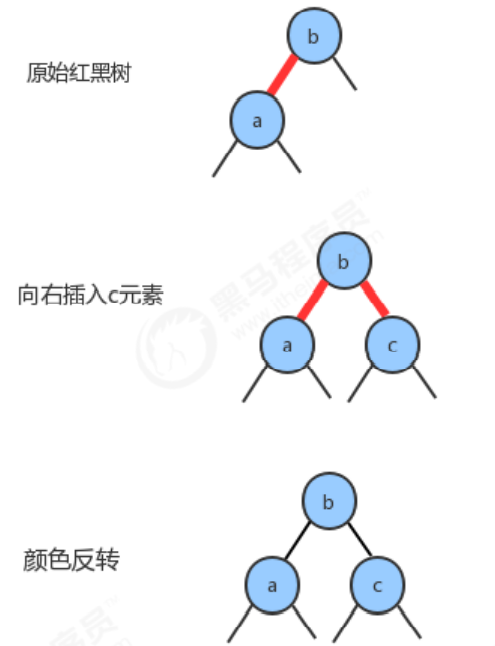
2. The new key is less than two keys in the original tree
   
   
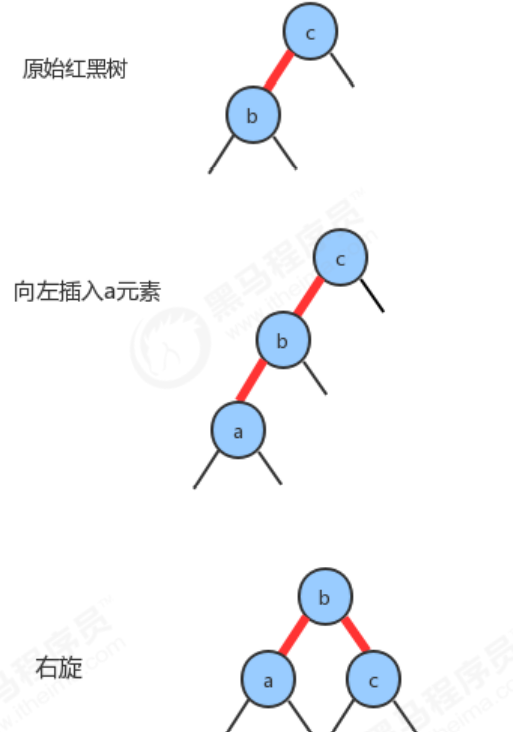
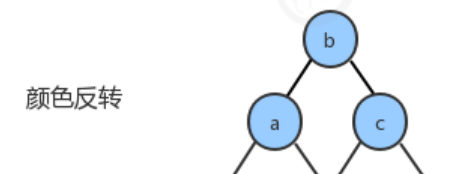
3. The new key is between two keys in the original number
   
   

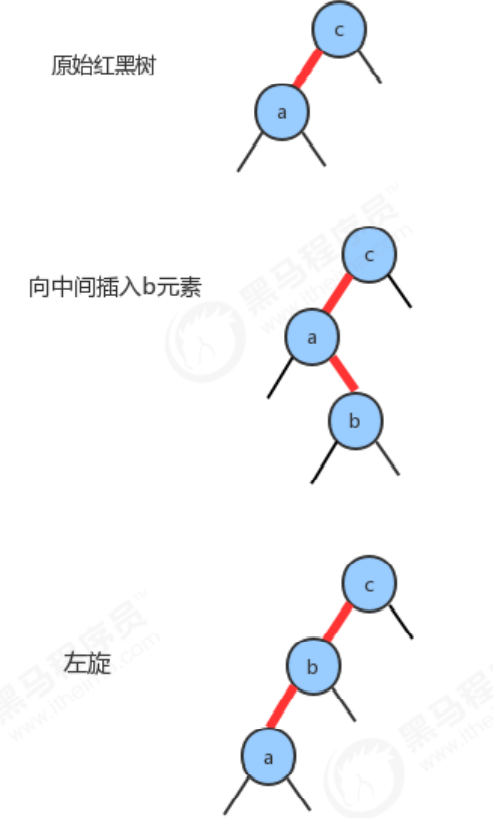
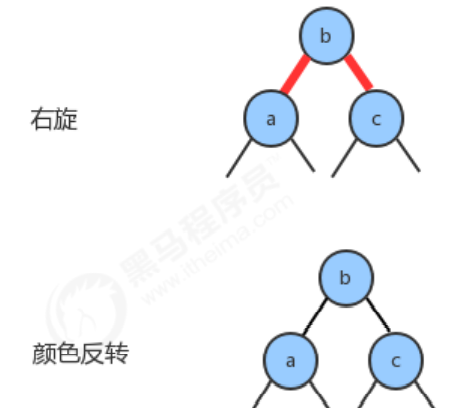
1.2.8 The color of the root node is always black

When we introduced the node API before, the color attribute in the Node object represents the color of the connection from the parent node to the current node. Since the root node does not have a parent node, after each insertion operation, we Both need to set the color of the root node to black.

1.2.9 Insert a new key to the 3-node at the bottom of the tree

Suppose a new node is added under a 3-node at the bottom of the tree. The three situations we mentioned above will occur. The link to the new node may be the right link of the 3-node (in this case we only need to convert the color), or the left link (in this case we need to rotate right and then convert), or the middle link (in this case When you need to first rotate to the left and then rotate to the right, and finally convert the color). The color conversion will make the color of the intermediate node red, which is equivalent to sending it to the parent node. This means that a new key continues to be inserted in the parent node, and we only need to use the same method to solve it until a 2-node or root node is encountered.

1.2.10 API design of red-black tree

1.2.11 Implementation of red-black tree

//红黑树代码
public class RedBlackTree<Key extends Comparable<Key>, Value> {
    
    
	//根节点
	private Node root;
	//记录树中元素的个数
	private int N;
	//红色链接
	private static final boolean RED = true;
	//黑色链接
	private static final boolean BLACK = false;
	/**
	* 判断当前节点的父指向链接是否为红色
	*
	* @param x
	* @return
	*/
	private boolean isRed(Node x) {
    
    
		//空结点默认是黑色链接
		if (x == null) {
    
    
			return false;
		}
		//非空结点需要判断结点color属性的值
		return x.color == RED;
	}
	/**
	* 左旋转
	*
	* @param h
	* @return
	*/
	private Node rotateLeft(Node h) {
    
    
		//找出当前结点h的右子结点
		Node hRight = h.right;
		//找出右子结点的左子结点
		Node lhRight = hRight.left;
		//让当前结点h的右子结点的左子结点成为当前结点的右子结点
		h.right = lhRight;
		//让当前结点h称为右子结点的左子结点
		hRight.left = h;
		//让当前结点h的color编程右子结点的color
		hRight.color = h.color;
		//让当前结点h的color变为RED
		h.color = RED;
		//返回当前结点的右子结点
		return hRight;
	}
	/**
	* 右旋
	*
	* @param h
	* @return
	*/
	private Node rotateRight(Node h) {
    
    
		//找出当前结点h的左子结点
		Node hLeft = h.left;
		//找出当前结点h的左子结点的右子结点
		Node rHleft = hLeft.right;
		//让当前结点h的左子结点的右子结点称为当前结点的左子结点
		h.left = rHleft;
		//让当前结点称为左子结点的右子结点
		hLeft.right = h;
		//让当前结点h的color值称为左子结点的color值
		hLeft.color = h.color;
		//让当前结点h的color变为RED
		h.color = RED;
		//返回当前结点的左子结点
		return hLeft;
	}
	/**
	* 颜色反转,相当于完成拆分4-节点
	*
	* @param h
	*/
	private void flipColors(Node h) {
    
    
		//当前结点的color属性值变为RED；
		h.color = RED;
		//当前结点的左右子结点的color属性值都变为黑色
		h.left.color = BLACK;
		h.right.color = BLACK;
	}
	/**
	* 在整个树上完成插入操作
	*
	* @param key
	* @param val
	*/
	public void put(Key key, Value val) {
    
    
		//在root整个树上插入key-val
		root = put(root, key, val);
		//让根结点的颜色变为BLACK
		root.color = BLACK;
	}
	/**
	* 在指定树中，完成插入操作,并返回添加元素后新的树
	*
	* @param h
	* @param key
	* @param val
	*/
	private Node put(Node h, Key key, Value val) {
    
    
		if (h == null) {
    
    
			//标准的插入操作，和父结点用红链接相连
			N++;
			return new Node(key, val, null, null, RED);
		}
		//比较要插入的键和当前结点的键
		int cmp = key.compareTo(h.key);
		if (cmp < 0) {
    
    
			//继续寻找左子树插入
			h.left = put(h.left, key, val);
		} else if (cmp > 0) {
    
    
			//继续寻找右子树插入
			h.right = put(h.right, key, val);
		} else {
    
    
			//已经有相同的结点存在，修改节点的值；
			h.value = val;
		}
		//如果当前结点的右链接是红色，左链接是黑色，需要左旋
		if (isRed(h.right) && !isRed(h.left)) {
    
    
			h=rotateLeft(h);
		}
		//如果当前结点的左子结点和左子结点的左子结点都是红色链接，则需要右旋
		if (isRed(h.left) && isRed(h.left.left)) {
    
    
			h=rotateRight(h);
		}
		//如果当前结点的左链接和右链接都是红色，需要颜色变换
		if (isRed(h.left) && isRed(h.right)) {
    
    
			flipColors(h);
		}
		//返回当前结点
		return h;
	}
	//根据key，从树中找出对应的值
	public Value get(Key key) {
    
    
		return get(root, key);
	}
	//从指定的树x中，查找key对应的值
	public Value get(Node x, Key key) {
    
    
		//如果当前结点为空，则没有找到,返回null
		if (x == null) {
    
    
			return null;
		}
		//比较当前结点的键和key
		int cmp = key.compareTo(x.key);
		if (cmp < 0) {
    
    
			//如果要查询的key小于当前结点的key，则继续找当前结点的左子结点；
			return get(x.left, key);
		} else if (cmp > 0) {
    
    
			//如果要查询的key大于当前结点的key，则继续找当前结点的右子结点；
			return get(x.right, key);
		} else {
    
    
			//如果要查询的key等于当前结点的key，则树中返回当前结点的value。
			return x.value;
		}
	}
	//获取树中元素的个数
	public int size() {
    
    
		return N;
	}
	//结点类
	private class Node {
    
    
		//存储键
		public Key key;
		//存储值
		private Value value;
		//记录左子结点
		public Node left;
		//记录右子结点
		public Node right;
		//由其父结点指向它的链接的颜色
		public boolean color;
		public Node(Key key, Value value, Node left, Node right, boolean color) {
    
    
			this.key = key;
			this.value = value;
			this.left = left;
			this.right = right;
			this.color = color;
		}
	}
}
//测试代码
public class Test {
    
    
	public static void main(String[] args) throws Exception {
    
    
		RedBlackTree<Integer, String> bt = new RedBlackTree<>();
		bt.put(4, "二哈");
		bt.put(1, "张三");
		bt.put(3, "李四");
		bt.put(5, "王五");
		System.out.println(bt.size());
		bt.put(1,"老三");
		System.out.println(bt.get(1));
		System.out.println(bt.size());
	}
}

Two B-trees

Earlier we have learned about binary search tree, 2-3 tree and its realization red-black tree. In the 2-3 tree, a node can have at most two keys, and its implementation red-black tree uses the way of coloring the links to express these two keys. Next, we learn another tree structure B-tree. In this data structure, a node allows more than two keys to exist.

A B-tree is a tree-like data structure that stores data, sorts it, and allows operations such as lookup, sequential read, insertion, and deletion with O(logn) time complexity.

2.1 Characteristics of B-tree

The B-tree allows a node to contain multiple keys, which can be 3, 4, 5 or even more. It is not sure, it depends on the specific implementation. Now we choose a parameter M to construct a B-tree, we can call it an M-order B-tree, then the tree will have the following characteristics:

• Each node has at most M-1 keys, and they are arranged in ascending order;
• Each node can have at most M child nodes;
• The root node has at least two child nodes;

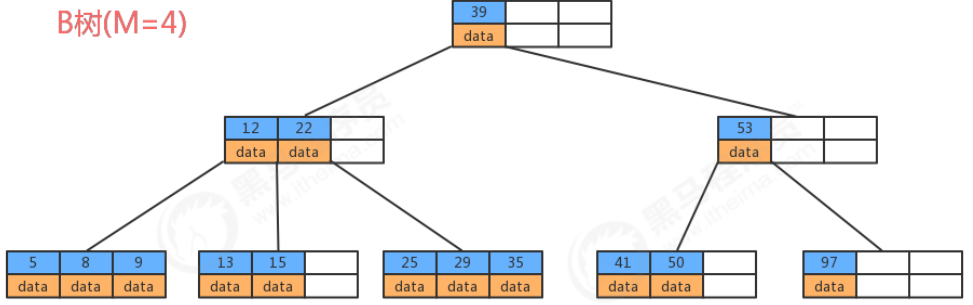
In practical applications, the order of the B-tree is generally relatively large (usually greater than 100), so even if a large amount of data is stored, the height of the B-tree is still relatively small, so that in some application scenarios, its advantages can be reflected .

2.2 B tree storage data

If the parameter M is selected as 5, then each node contains at most 4 key-value pairs. Let's take the 5th-order B-tree as an example to see the data storage of the B-tree.

2.3 Application of B-tree in disk files

In our program, it is inevitable to operate files through IO, and our files are stored on disk. The computer operates the files on the disk through the file system, and the B-tree data structure is used in the file system.

2.3.1 Disk

The disk can save a large amount of data, ranging from GB to TB, but its reading speed is relatively slow, because it involves machine operations, and the reading speed is at the millisecond level.

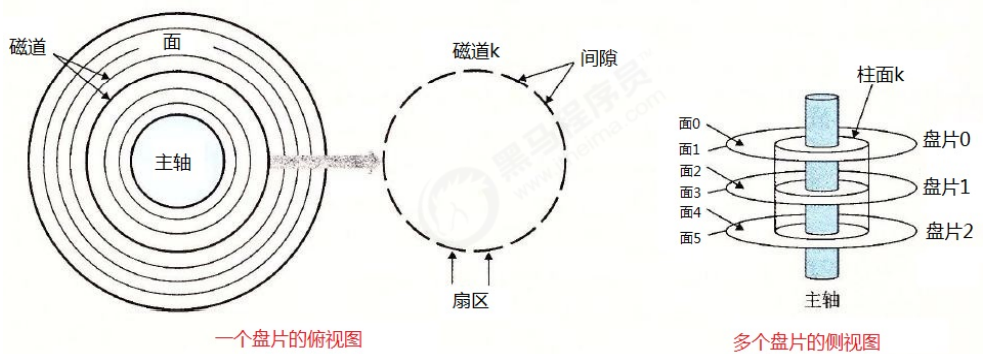
A disk is made up of platters, each platter has two sides, also known as a platter. There is a rotatable spindle in the center of the disc, which makes the disc rotate at a fixed rotation rate, usually 5400rpm or 7200rpm, and a disc contains multiple such discs and is packaged in a sealed container. Each surface of the platter is composed of a set of concentric circles called tracks, each track is divided into a set of sectors, each sector contains an equal number of data bits, usually 512 subsections, between sectors separated by gaps in which no data is stored.

2.3.2 Disk I/O

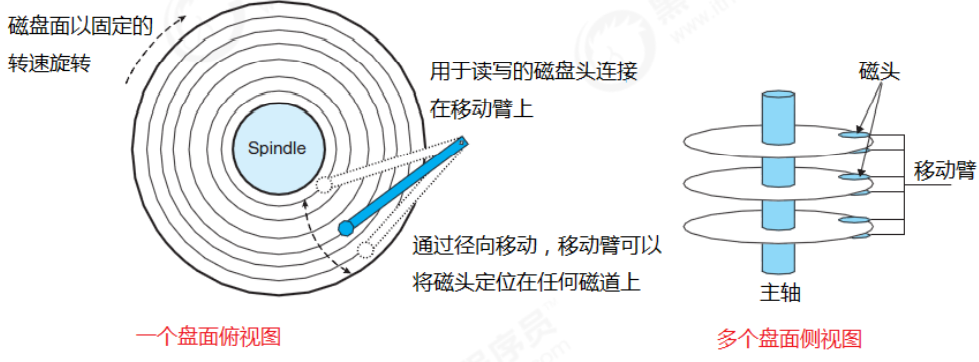
Disks use a head to read and write bits stored on the platter's surface. The head is attached to a moving arm that moves back and forth along the radius of the platter to position the head on any track. This is called a seek operation. Once located on the track, the platter rotates, and when each bit on the track passes the head, the read-write head can perceive the value of the bit, and can also modify the value. The access time to the disk is divided into seek time, rotation time, and transfer time.

Due to the characteristics of the storage medium, the access of the disk itself is much slower than that of the main memory, coupled with the cost of mechanical movement, so in order to improve efficiency, it is necessary to minimize disk I/O and reduce read and write operations. In order to achieve this goal, the disk is often not strictly read on demand, but reads ahead every time. Even if only one byte is needed, the disk will start from this position and sequentially read a certain length of data backwards into the memory. The rationale for this is the well-known computer science

The principle of locality: When a piece of data is used, the nearby data is usually used immediately. Because of the high efficiency of sequential disk reads (no seek
time, very little rotation time), read-ahead can improve I/O efficiency.

A page is a logical block of computer management memory. Hardware and operating systems often divide the main memory and disk storage area into continuous blocks of equal size. Each storage block is called a page (1024 bytes or its integer multiples). The read length is generally an integer multiple of pages. Main memory and disk exchange data in units of pages. When the data to be read by the program is not in the main memory, a page fault exception will be triggered. At this time, the system will send a read signal to the disk, and the disk will find the starting position of the data and continuously read one or several pages backwards. Load it into memory, then return abnormally, and the program continues to run.

The designer of the file system uses the principle of disk read-ahead to set the size of a node equal to a page (1024 bytes or an integer multiple thereof), so that each node can be fully loaded with only one I/O . Then the 3-layer B-tree can hold 1024 1024 1024 almost 1 billion data. If it is replaced with a binary search tree, it needs 30 layers! Assuming that the operating system reads one node at a time, and the root node is kept in memory, then the B-tree can find the target value in 1 billion data, and it only needs less than 3 hard disk reads to find the target value, but the red-black tree needs to be less than 30 times, so the B-tree greatly improves the operation efficiency of IO.

Triple B+ tree

The B+ tree is a modified tree of the B tree. The difference between it and the B tree is:

1. Non-leaf nodes only have an index function, that is, non-leaf nodes only store keys, not values;
2. All the leaf nodes of the tree form an ordered linked list, and all data can be traversed in the order of key sorting.

3.1 B+ tree storage data

If the parameter M is selected as 5, then each node contains at most 4 key-value pairs. Let's take the 5th-order B+ tree as an example to see the data storage of the B+ tree.

2.2 Comparison of B+ tree and B tree

The advantages of the B+ tree are:
1. Since the B+ tree does not contain real data on the non-leaf nodes and is only used as an index, it can store more keys with the same memory. 2. The leaf nodes of the B+ tree are all connected, so the traversal of the entire tree only requires a linear traversal of the leaf nodes. And because the data is arranged in sequence and connected, it is convenient for interval search and search. The B-tree requires recursive traversal of each layer.

The advantage of the B-tree is:
since each node of the B-tree contains key and value, when we search for the value based on the key, we only need to find the location of the key to find the value, but the B+ tree only stores data in leaf nodes. Every time the index is searched, it must find the maximum depth of the tree, that is, the depth of the leaf node, to find the value.

3.3 Application of B+ tree in database

In the operation of the database, the query operation can be said to be the most frequent operation. Therefore, when designing the database, the efficiency of the query must be considered. In many databases, B+ trees are used to improve the efficiency of the query;

When operating the database, in order to improve query efficiency, we can build an index based on a certain field of a table to improve query efficiency. In fact, this index is realized by the data structure of B+ tree.

3.3.1 No primary key index query

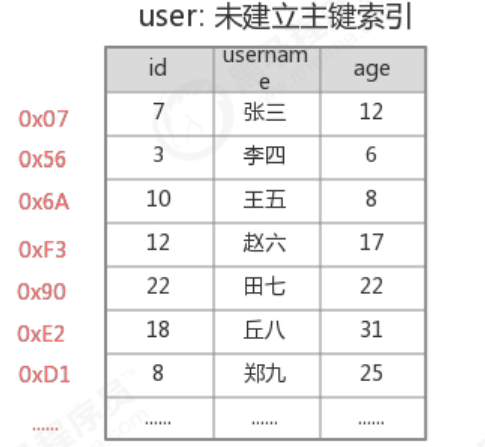
Execute select * from user where id=18, you need to start from the first piece of data, and go all the way to the 6th piece of data, and find id=18, then you can query the target result, and you need to compare 6 times in total;

3.3.2 Create primary key index query

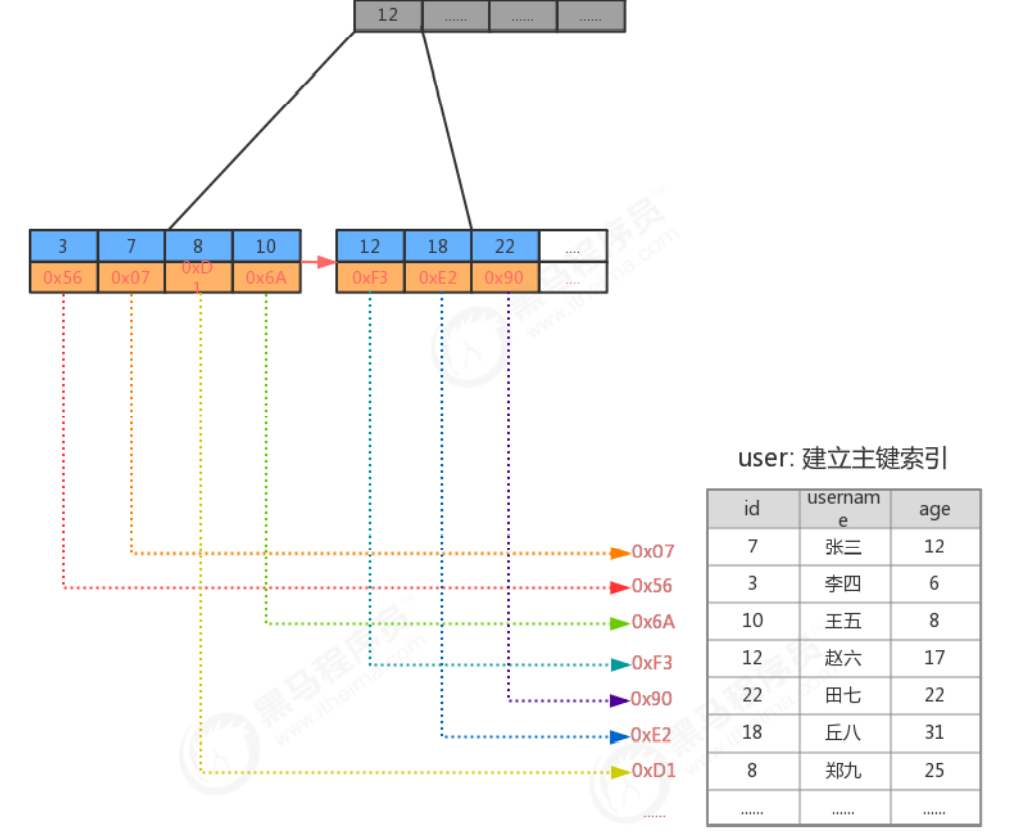
3.3.3 Range query

Execution select * from user where id>=12 and id<=18, if there is an index, since the leaf nodes of the B+ tree form an ordered linked list, we only need to find the leaf node with an id of 12, and search backwards in the order of traversing the linked list, which is very efficient.