Cryptography: public key cryptography.
Public Key Cryptography (Public Key Cryptography), also known as asymmetric cryptography , its biggest feature is that encryption and decryption no longer use the same key , but use different keys. The user will make one key public and the other key privately. At this time, the two keys are called the public key and the private key . Generally speaking, the public key and the private key are difficult to calculate each other, but they can be used as encryption and decryption keys respectively. When the information sender chooses to use the receiver's public key to encrypt, the receiver uses his own private key to decrypt the information after receiving the information, so that the confidentiality of the information can be maintained; if the information sender uses his own private key to encrypt the information summary , the receiver uses the sender's public key to verify the digest, which can play the role of a signature, which can ensure the authenticity and non-repudiation of the information.
Table of contents:
Cryptography: Public Key Cryptography
(2) Low encryption index and small plaintext attack
(5) Low resolution index attack (Wiener's Attack)
(6)Coppersmith's High Bits Attack
Discrete logarithm related cryptography:
(2) Calculation of discrete logarithm
2. More efficient computing methods
RSA algorithm:
The RSA algorithm is the most widely used public-key cryptographic algorithm in engineering . The security of the algorithm is based on a simple mathematical fact: For large prime numbers p and q, it is very simple to calculate n = pxq, but factoring it when n is known Getting p and q is quite difficult.
Online RSA algorithm encryption and decryption: RSA online encryption and decryption - RSA key generator
The basic algorithm of RSA is as follows: Select a larger index p and q (generally greater than 512bit, and p is not equal to q), and calculate:
n = p x q
The correctness of the encryption and decryption algorithm is proved as follows:

so:

Common attacks on RSA:
(1) Factorization:
Since only p, g and e are used in the RSA private key generation process, if p and q are successfully obtained, then the private key modulus d can be calculated using normal calculation methods. If the size of n is not too large (not larger than 512 bits), it is recommended to try factorization first. Commonly used auxiliary tools for factorization include SageMath, Yafu, and the online factor query website factordb.
In addition, if the difference between p and 9 is very small, due to

You can decompose pq by enumerating the value of p - g violently.
For example, for the RSA public key <n, e>=<16422644908304291, 65537>, since the value of is small, the factorization method can be considered. Use Yafu to execute factor (16422644908304291) and get the following output:
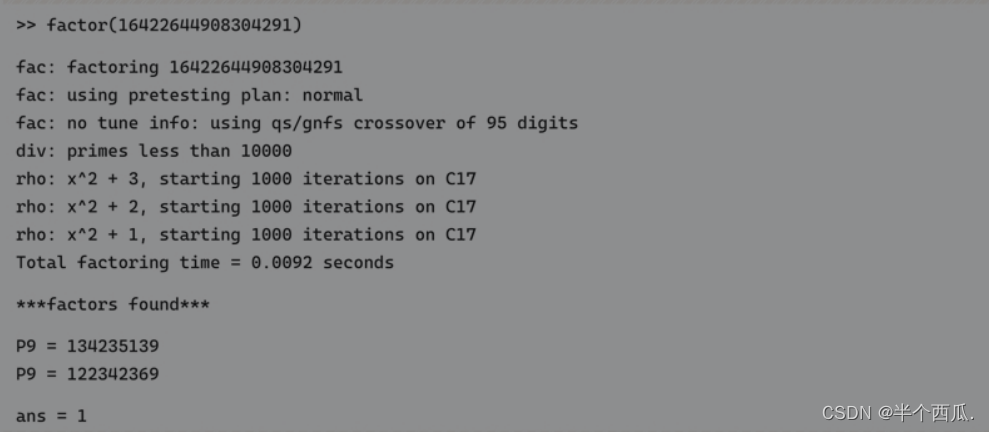
Thus, the two prime numbers p and q are 134235139 and 122342369 respectively. The value of the private key a can be calculated using the Gmpy2 Python library.

(2) Low encryption index and small plaintext attack
If the encrypted m is very small and e is small, so that the encrypted c is still smaller than n, then the ciphertext can be directly raised to the power of e to obtain the plaintext m. For example, consider the following case: n=100000980001501, e=3, m=233, then pow(m, e) = 12649337, still less than n. At this time, the 3rd power of 12649337 can solve the plaintext 233.
If the encrypted c is larger than n but not too large, since pow (m, e) = kn+c, k can be enumerated violently, and then the e power can be opened until the e power can be opened, and the solution is correct up to C. For example, when r and e are the same as above, but m = 233333, there is C = pow(m, e, n) = 3524799146410.
The code to enumerate the coefficients of n using Python is as follows:

When k=127 is enumerated, the third power can be exhausted, and the plaintext is 233333;
(3) Common mode attack
If the same n is used, different moduli e1, e2, and e1, e2 are mutually prime, and the same set of plaintext is encrypted to obtain ciphertext c1, c2, then the plaintext m can be calculated without calculating the private key. set up


Obviously, the same m is encrypted with the same n and different e to get different c, and the two e are mutually prime, you can try to solve m with the method of common mode attack.
First, use the extended Euclidean algorithm to find x and y in xe1+ye2=1:



The plaintext m can be solved without decomposing n. Since the time complexity of the extended Euclidean algorithm is O(logn), when n is very large
, this method is still available.
If you encounter a situation where there is only one set of plaintext but multiple ciphertexts are encrypted by multiple e, you should first consider using a common mode attack.
(4) Broadcast attack
For the same plaintext m, using the same exponent e and different modulus n1, n2, ..., ni, when encrypting to get i group of ciphertexts (i ≥ e), the plaintext can be deciphered by using the Chinese remainder theorem. set up
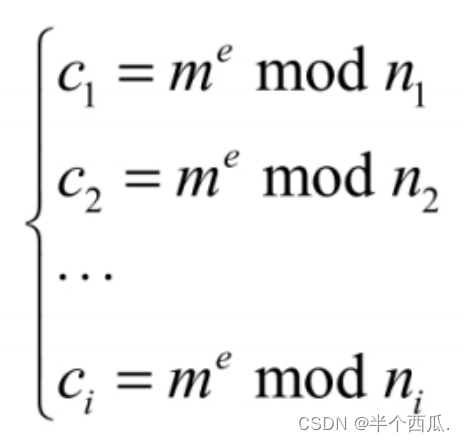
Simultaneous equations, using the Chinese remainder theorem, can find a Cx that satisfies

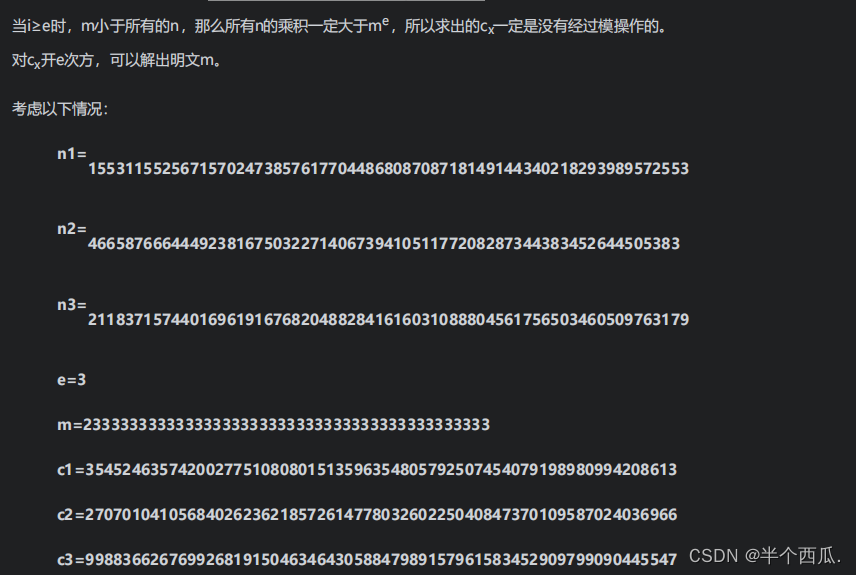
Let's try to use a broadcast attack to solve n. Simultaneously three systems of equations, using the Chinese remainder theorem:

It can be seen that we successfully decoded the plaintext.
If you see multiple encryptions with the same e but different n and e is small, and the number of ciphertext groups is not less than e, you should consider using this method.
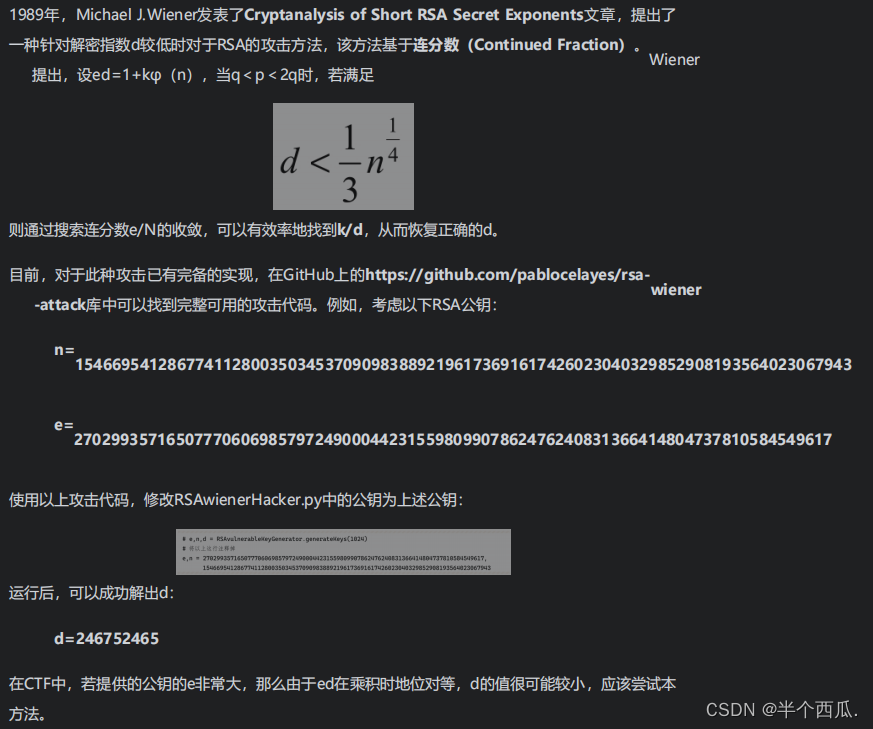
(5) Low resolution index attack (Wiener's Attack)
(6)Coppersmith's High Bits Attack
This method was proposed by Don Coppersmith. If a large part of the plaintext is known, that is, m=motx, and mo or the high bits of a large prime number in n are known, the private key can be attacked. Generally, for a large prime number of 1024 bits, only 640 bits need to be known to successfully attack. For the detailed implementation of the attack, see: GitHub - mimoo/RSA-and-LLL-attacks: attacking RSA via lattice reductions (LLL)
(7)RSA LSB Oracle



Discrete logarithm related cryptography:
(1) EIGamal and ECC


(2) Calculation of discrete logarithm
1. Brute Force Computing
When the value of p is not too large, since the value of the discrete logarithm must be in the range of 0 to p-1, it is obviously possible to exhaustively. For example, consider the following situation:

The following brute force calculation code can be written:

Below is an example of bruteforcing an elliptic curve discrete logarithm. Consider the following curves and points, and find logpQ:

Define the circular curve and the two points P and Q in Sagemath, write out the cycle, and then brute force can be cracked:

The time complexity of this method is O (n) , when p is less than 1e7 order of magnitude, violent calculation can be considered.
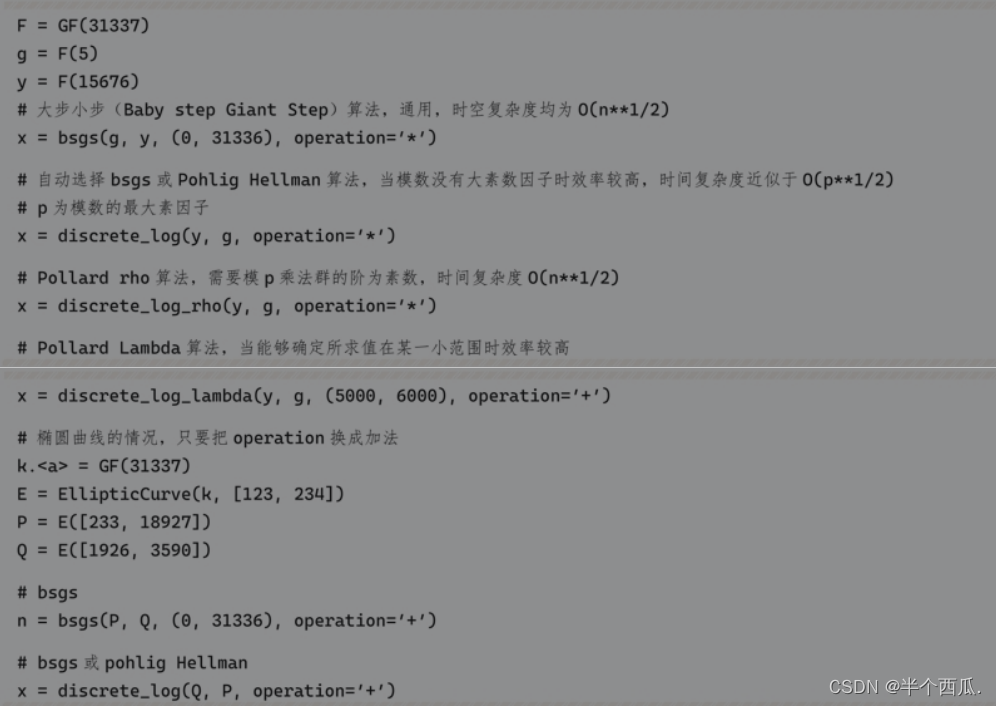
2. More efficient computing methods
Sagemath has built-in different kinds of discrete logarithm calculation methods, which are suitable for various occasions. The following code introduces some commonly used algorithms for calculating discrete logarithms. For specific usage conditions, please refer to the code comments.
Learning Books: From 0 to 1: CTFer Growth Road...

