[Algorithms | Short answers to examples] Explanation of relevant examples

Indirect recursion : function g is called in the definition of a function f, and function f is called in the definition of function g. Elimination of recursion is generally implemented with a stack.

3. The design idea of the divide and conquer method is to divide a large problem that is difficult to solve directly into smaller sub-problems, solve the sub-problems separately, and finally combine the solutions of the sub-problems to form the solution of the original problem. This requires the original question and subquestions:

The scale of the problem is different, but the nature of the problem is the same.

4. In the problem of finding the kth smallest element among n elements, such as the idea of quick sort algorithm, divide n elements by using the divide and conquer algorithm, how to choose the division criterion?

Randomly select an element as the division basis, take the first element of the subsequence as the division basis, and use the median method of the median to find the division basis.

5. The quick sort algorithm is designed according to the divide and conquer strategy, and its basic idea is briefly described.

For quick sorting of the unordered sequence a[low..high], the whole sorting is "big problem". Select one of the bases base=a[i] (usually based on the first element in the sequence), move all elements less than or equal to base to its front, and all elements greater than or equal to base to move behind it, that is, The benchmark is homing to a[i], which produces two unordered sequences, a[low..i-1] and a[i+1..high], whose ordering is a "small problem". When the a[low..high] sequence has only one element or is empty, it corresponds to the recursive exit.

Therefore, the quick sort algorithm uses a divide-and-conquer strategy to decompose a "big problem" into two "small problems" to solve. Since the elements are all in the a array, the merging process is naturally generated without special design.

6. Assuming that the data a to be sorted containing n elements happens to be sorted in descending order, it means that the time complexity of calling QuickSort(a, 0, n-1) for ascending sorting is O( ) $n^{2}$ .

At this time, the height of the recursive tree corresponding to quick sorting is O(n), and the time corresponding to each division is O(n), and the entire sorting time is O( $n^{2}$ ).

7. Which algorithms use divide and conquer strategy.

Among them, the two-way merge sort and the binary search algorithm adopt the divide and conquer strategy.

8. What are the characteristics of problems suitable for parallel computing?

1) Separating work into discrete parts helps to solve simultaneously. For example, for a serial algorithm designed by the divide and conquer method, each independent sub-problem can be solved in parallel, and finally merged into the solution of the whole problem, so as to be transformed into a parallel algorithm.
2) Execute multiple program instructions at any time and in a timely manner.
3) It takes less time to solve the problem under multiple computing resources than under a single computing resource.

9. There are two complex numbers x=a+bi and y=c+di. The complex product xy can be done using 4 multiplications, ie xy=(ac-bd)+(ad+bc)i. Design a method to compute the product xy using only 3 multiplications.

xy=(ac-bd)+((a+b)(c+d)-ac-bd)i. It can be seen that calculating xy in this way requires only 3 multiplications (ie ac, bd and (a+b)(c+d) multiplications).

10. There are 4 arrays a, b, c and d, all of which have been sorted, explain the method of finding the intersection of these 4 arrays.

Using the basic two-way merge idea, first find the intersection ab of a and b, then find the intersection cd of c and d, and finally find the intersection of ab and cd, which is the final result. It can also be solved directly by using the 4-way merge method.

11. Briefly compare brute force and divide and conquer.

The brute force method is a simple and direct method to solve problems. It has a wide range of applications and is a general method that can solve almost all problems. It is often used in some very basic but very important algorithms (sorting, searching, matrix multiplication and character String matching, etc.), the brute force method mainly solves some small-scale or low-value problems, and can be used as a standard for more efficient algorithms for the same problem. The divide and conquer method adopts the idea of divide and conquer, which divides a complex problem into two or more identical or similar sub-problems, and then divides the sub-problems into smaller sub-problems until the problem is solved. The divide and conquer method usually performs better than the brute force method in solving problems.

12. Under what circumstances is recursion used when using the brute force method to solve?

If the problem solved by the brute force method can be decomposed into several smaller similar sub-problems, then recursion can be used to implement the algorithm

13. In the solution space tree of the problem in the backtracking method, what strategy is used to search the solution space tree from the root node?

depth first

14. The wrong statement about the backtracking method is

The backtracking algorithm needs to use the queue structure to save the path from the root node to the current extended node

15. What factors does the efficiency of the backtracking method depend on?

The number of values that satisfy the explicit constraint, the time to calculate the constraint function, and the time to calculate the bound function

16. What function is the strategy adopted in the backtracking method to avoid invalid searches?

pruning function

17. What are the search characteristics of the backtracking method?

The backtracking method uses the depth-first traversal method in the solution space tree to search for solutions, that is, uses constraints and boundary functions to examine the value of the solution vector element x[i], and if x[i] is reasonable, search for x[i] as For the subtree of the root node, if x[i] has taken all the values, it will go back to x[i-1].

18. When using the backtracking method to solve the 0/1 knapsack problem, what is the structure of the solution space of the problem? When using the backtracking method to solve the pipeline job scheduling
problem, what is the structure of the solution space of the problem?

When using the backtracking method to solve the 0/1 knapsack problem, the solution space of the problem is a subset tree structure. When using the backtracking method to solve the pipeline job scheduling problem, the solution space of the problem is a permutation tree structure.

19. For the increasing sequence a[]={1, 2, 3, 4, 5}, use the backtracking method to find the full arrangement, must the arrangement starting with 1 and 2 appear first? Why?

Yes. The corresponding solution space is a permutation tree. As shown in the figure, the first three layers are shown. Obviously, the first permutations are the leaf nodes extended from the G node, and they are permutations starting with 1 and 2.

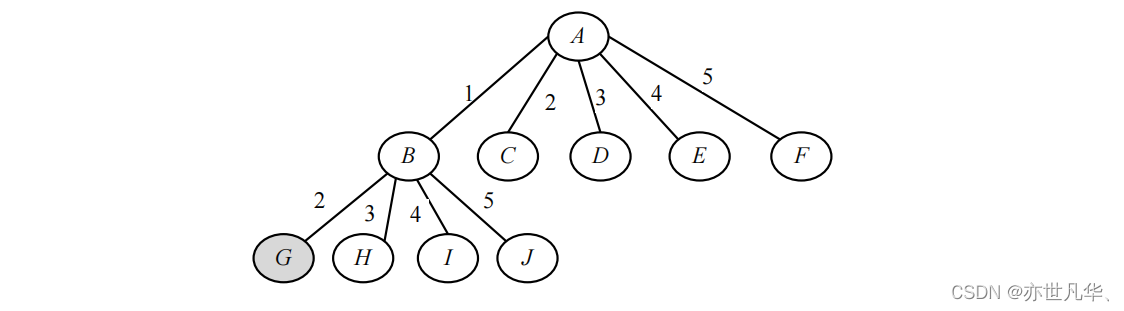
20. Consider the problem of n queens, the solution space tree is composed of n! sorts of permutations consisting of 1, 2, ..., n. Now use the backtracking method to solve it as follows:

(1) According to the solution search space, there is no solution when n=3.

The solution search space when n=3 is shown in the figure, and no leaf nodes can be obtained, so there is no solution.

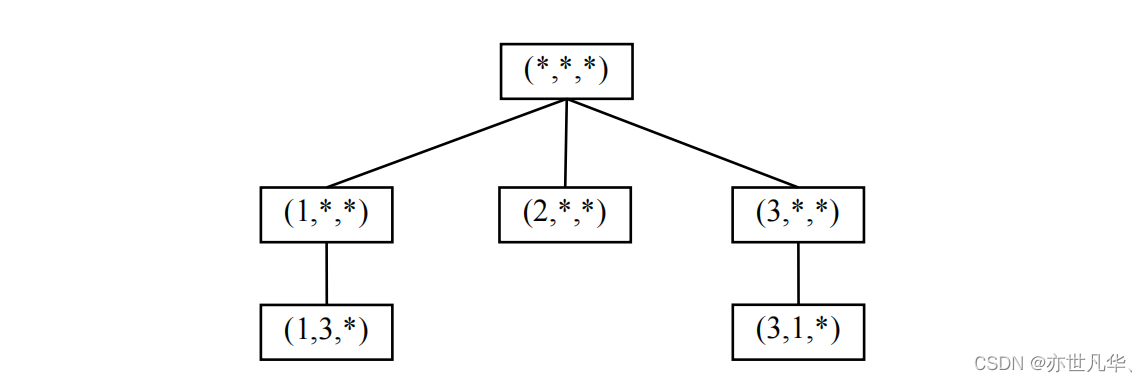
(2) Give the pruning operation.

The pruning operation is that any two queens cannot be in the same row, the same column and the same two diagonals.

(3) How many nodes will be generated on the solution space tree in the worst case? Analyze the time complexity of the algorithm.

In the worst case, each node expands n nodes, there are a total $n^{n}$ of nodes, and the time complexity of the algorithm is O( $n^{n}$ )

21. Branch and Bound method In the solution space tree of the problem, what strategy is used to search the solution space tree from the root node.

breadth first

22. Two common branch and bound methods are:

Queue (FIFO) branch-and-bound method and priority queue-type branch-and-bound method.

23. When the branch and bound method is used to solve the 0/1 knapsack problem, the organization form of the slipnode table is

Dagendui

24. The algorithm using the maximum benefit first search method is

branch and bound

25. The principle of selecting extended nodes in the priority queue branch-and-bound method is

node priority

26. Briefly describe the search strategy of the branch and bound method.

The search strategy of the branch and bound method is breadth-first traversal, and a solution or an optimal solution can be quickly found through the bound function.

27. There is a 0/1 knapsack problem, where n=4, the weight of the item is (4, 7, 5, 3), the value of the item is (40, 42, 25, 12), and the maximum carrying capacity of the knapsack is W=10. The process of using the priority queue branch and bound method to find the optimal solution is presented.

The solution process is as follows:
1) Root node 1 enters the queue, corresponding node values: ei=0, ew=0, ev=0, e.ub=76, x:[0, 0, 0, 0].
2) Dequeue node 1: left child node 2 enters the queue, corresponding node values: e.no=2, ei=1, ew=4, ev=40, e.ub=76, x:[1, 0, 0, 0]; right child node 3 enters the team, corresponding node value: e.no=3, ei=1,
ew=0, ev=0, e.ub=57, x:[0,0 ,0,0].
3) Dequeue node 2: the left child is overweight; the right child node 4 enters the queue, corresponding node values: e.no=4, ei=2, ew=4, ev=40, e.ub=69, x :[1, 0, 0, 0].
4) Dequeue node 4: left child node 5 enters the queue, corresponding node values: e.no=5, ei=3, ew=9, ev=65, e.ub=69, x:[1, 0, 1, 0]; right child node 6 enters the team, corresponding node value: e.no=6, ei=3, ew=4, ev=40, e.ub=52, x:[1,0 ,0,0].
5) Dequeue node 5: Generate a solution, maxv= 65, bestx: [1, 0, 1, 0].
6) Dequeue node 3: left child node 8 enters the queue, corresponding node values: e.no=8, ei=2, ew=7, ev=42, e.ub=57, x:[0, 1, 0, 0]; the right child node 9 is pruned.
7) Dequeue node 8: the left child is overweight; the right child node 10 is pruned.
8) Dequeue node 6: the left child node 11 is overweight; the right child node 12 is pruned.
9) The queue is empty, the algorithm ends, and the optimal solution generated: maxv= 65, bestx: [1, 0, 1, 0].

28. There is a pipeline job scheduling problem, n=4, a[]={5, 10, 9, 7}, b[]={7, 5, 9, 8}, given the priority queue type branch and bound The process of finding a solution.

The solution process is as follows:
1) Root node 1 enters the queue, corresponding node values: ei=0, e.f1=0, e.f2=0, e.lb=29, x: [0, 0, 0, 0 ].
2) Dequeue node 1: expand the nodes as follows:
enter the queue (j=1): node 2, ei=1, e.f1=5, e.f2=12, e.lb=27, x: [ 1, 0, 0, 0].
Enter the queue (j=2): node 3, ei=1, e.f1=10, e.f2=15, e.lb=34, x: [2, 0, 0, 0].
Entering the queue (j=3): node 4, ei=1, e.f1=9, e.f2=18, e.lb=29, x: [3, 0, 0, 0].
Entering the queue (j=4): node 5, ei=1, e.f1=7, e.f2=15, e.lb=28, x: [4, 0, 0, 0].
3) Dequeue node 2: expand the nodes as follows:
enter the queue (j=2): node 6, ei=2, e.f1=15, e.f2=20, e.lb=32, x: [ 1, 2, 0, 0].
Entering the queue (j=3): node 7, ei=2, e.f1=14, e.f2=23, e.lb=27, x: [1, 3, 0, 0].
Entering the queue (j=4): node 8, ei=2, e.f1=12, e.f2=20, e.lb=26, x: [1, 4, 0, 0].
4) Dequeue node 8: expand the nodes as follows:
enter the queue (j=2): node 9, ei=3, e.f1=22, e.f2=27, e.lb=31, x: [ 1, 4, 2, 0].
Enter the queue (j=3): node 10, ei=3, e.f1=21, e.f2=30, e.lb=26, x: [1, 4, 3, 0].
5) Dequeue node 10, expand a child node of j=2, have ei=4, reach the leaf node, and generate a solution
is e.f1=31, e.f2=36, e.lb=31, x=[1, 4, 3, 2].
The scheduling scheme corresponding to this solution is: execute job 1 in the first step, execute job 4 in the second step, execute job 3 in the third step
, execute job 2 in the fourth step, and the total time=36.

29. The basic elements of the greedy algorithm are

greedy choice property

30. What problems cannot be solved using the greedy method.

n queen problem

31. The main calculation of the optimal loading problem using the greedy algorithm is to sort the containers according to their weight from small to large, so the time complexity of the algorithm is

O(nlog2n)

32. About the 0/1 knapsack problem

For the same backpack and the same items, the total value obtained by doing the knapsack problem must be greater than or equal to doing the 0/1 knapsack problem.

33. A Huffman tree has a total of 215 nodes, and Huffman coding is performed on it, and a total of ( ) different codewords can be obtained.

108

34. How to reflect greedy thinking in solving Huffman coding?

When constructing the Huffman tree, the two trees with the smallest root nodes are merged each time, thus reflecting the idea of greed.

35. Give a counter-example to prove the 0/1 knapsack problem. If the algorithm used is to consider the selected items in the non-decreasing order of vi/wi, that is, as long as the items being considered can be loaded into the knapsack, this method may not necessarily get Optimal solution (this question shows the difference between the 0/1 knapsack problem and the knapsack problem).

For example, when n=3, w={3, 2, 2}, v={7, 4, 4}, W=4, since 7/3 is the largest, if you follow the method required by the title, you can only take the first one, The payoff is 7. And the maximum benefit of this example should be 8, take the 2nd and 3rd items.

36. The optimal solution is usually solved in a bottom-up manner

dynamic programming

37. What kind of algorithm is the memorandum method?

dynamic programming

38. The basic elements of dynamic programming algorithm are.

Subproblem Overlapping Properties

39. The key characteristics of a problem that can be solved by a dynamic programming algorithm or a greedy algorithm are the problems:

Optimal Substructure Properties

40. Briefly describe the basic idea of dynamic programming method.

The basic idea of the dynamic programming method is to decompose the problem to be solved into several sub-problems, first find the solution of the sub-problems, and then obtain the solution of the original problem from the solutions of these sub-problems.

41. Briefly describe the similarities and differences between the dynamic programming method and the greedy method.

The three basic elements of the dynamic programming method are the optimal substructure property, no aftereffect and overlapping subproblem properties, while the two basic elements of the greedy method are the greedy selection property and the optimal substructure property. So both of them have in common that they both require the problem to have the optimal substructure property.
The differences between the two are as follows:
(1) The solution methods are different. The dynamic programming method is bottom-up. Some problems with optimal substructure properties can only be used by the dynamic programming method, and some can be used by the greedy method. The greedy method is top-down.
(2) The dependence on the sub-problems is different. The dynamic programming method depends on the solution of each sub-problem, so each sub-problem should be optimized to ensure the overall optimality; while the greedy method depends on the choices made in the past, but never Depends on future choices and does not depend on solutions to subproblems.

42. Briefly describe the similarities and differences between dynamic programming and divide and conquer.

What both have in common:

It is to decompose the problem to be solved into several sub-problems, solve the sub-problems first, and then obtain the solution of the original problem from the solutions of these sub-problems.

The difference between the two is:

It is suitable for problems solved by dynamic programming method. The sub-problems obtained by decomposition are often not independent of each other (the nature of overlapping sub-problems), while the sub-problems in the divide-and-conquer method are independent of each other; in addition, the dynamic programming method uses a table to save the solved sub-problems The solution of the problem does not need to be solved again when encountering the same sub-problem again, but only needs to query the answer, so polynomial time complexity can be obtained, and the efficiency is high. In the divide and conquer method, each sub-problem that appears is solved, Causes the same sub-problem to be solved repeatedly, so the time complexity of exponential growth is generated, and the efficiency is low

43. Which ones belong to the dynamic programming algorithm?

Judging whether the algorithm has the properties of optimal substructure, no aftereffect and overlapping subproblems. Direct insertion sorting algorithm, simple selection sorting algorithm and two-way merge sorting algorithm are dynamic programming algorithms.

Calculation problems

Calculation of Time Complexity

one,

two,

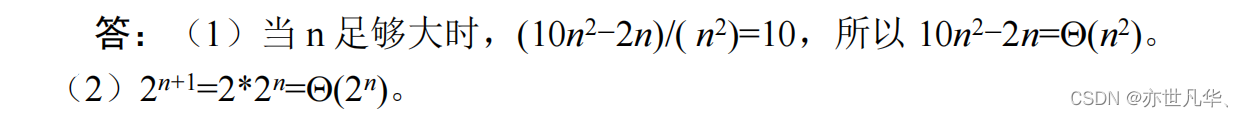
three,

Recursive algorithm calculation

one,

two,

three,

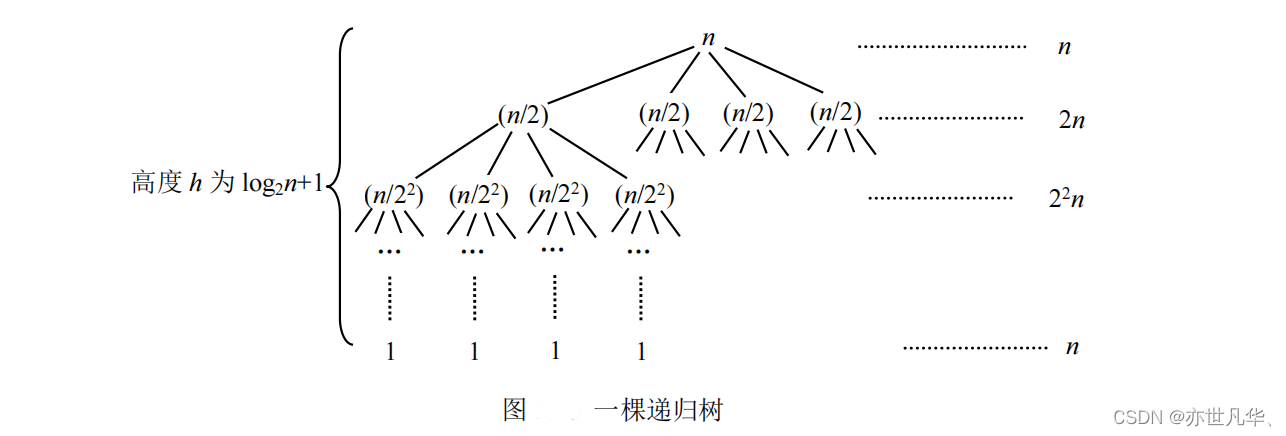
Four,

five,

six,

Knapsack problem (0-1 knapsack problem)

Backtracking

dynamic programming

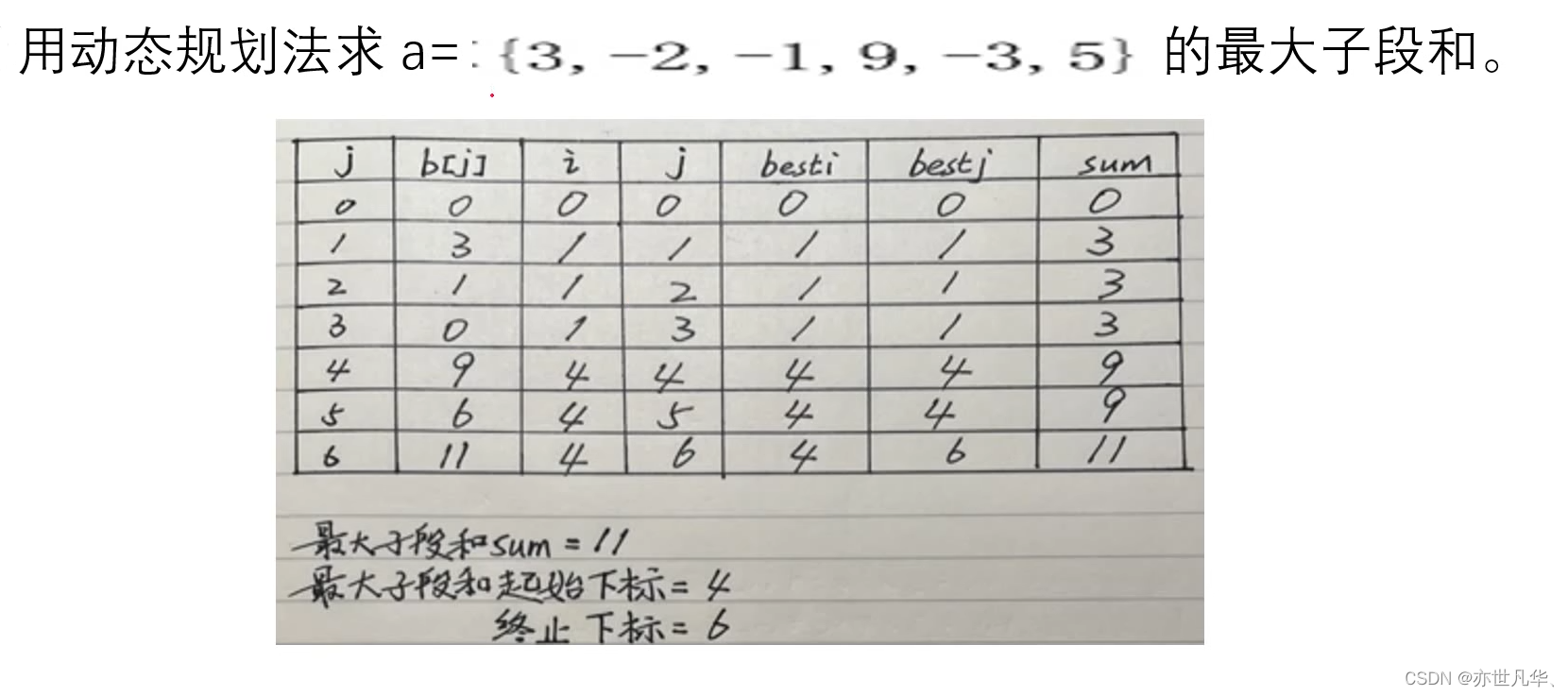
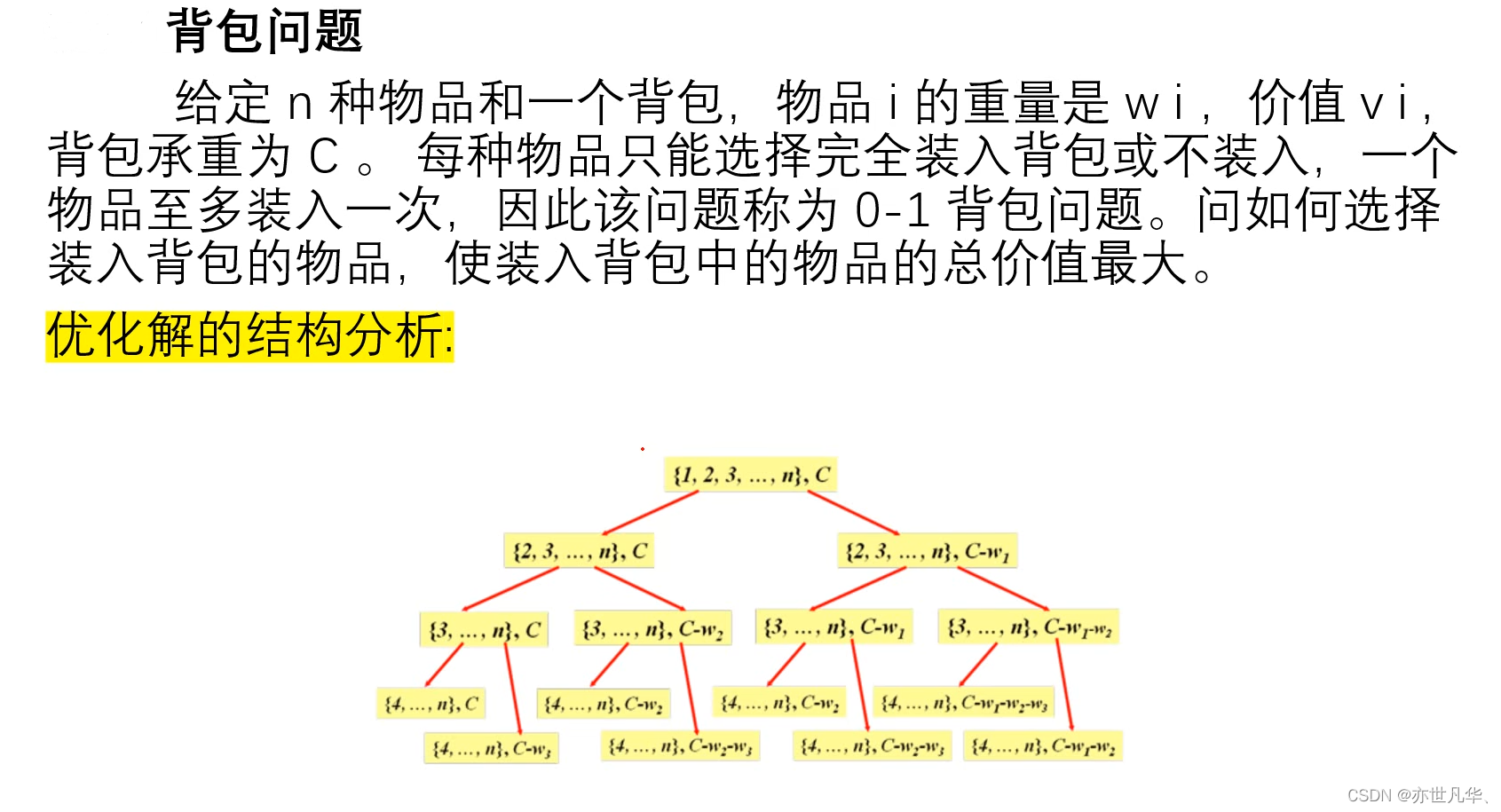
programming questions

Solving Equations Using Backtracking

#include<iostream>
using namespace std;

int a[6] = { 0 };
int solution(int b[], int m, int n)
{
    if (m == n)
    {
        if (b[0] * b[1] - b[2] * b[3] - b[4] == 1)
        {
            printf("解为a=%d b=%d c=%d d=%d e=%d\n", b[0], b[1], b[2], b[3], b[4]);
        }
        return 0;
    }
    for (int i = 1; i <= n; i++)
    {
        if (a[i] == 0)
        {
            a[i] = 1;
            b[m] = i;
            solution(b, m + 1, n);
            a[i] = 0;
        }
    }
}
int main()
{
    int c[6];
    solution(c, 0, 5);
    return 0;
}

Dynamic Programming Method to Solve Spiders Eating Mosquitoes

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cstdlib>

int main(int argc, char** argv)
{
	int n = 5, i, j;
	if (argc == 2)	n = std::stoi(argv[1]);
	std::vector<std::vector<int> >  dp(n, std::vector<int>(n, 1));

	for (i = 1; i < n; ++i)
		for (j = 1; j < n; ++j)
		{
			dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
		}

	std::cout << "total path for " << n << "x" << n << " grid: " << dp[n - 1][n - 1] << std::endl;
	return 0;
}

Divide and Conquer to Solve the Coin Toss Problem

#include <iostream>
#include <vector>
#include <string>
#include <cstdlib>
#include <numeric>
#include <time.h> 

int solve(std::vector<int>& a, int low, int high);

int main(int argc, char** argv)
{
	int n = 100, m, ans;
	if (argc == 2)	n = std::stoi(argv[1]);
	std::vector<int> a(n, 2);
	srand((unsigned)time(NULL));
	m = rand() % n;	std::cout << "m: " << m << std::endl;
	a[m] = 1;
	std::cout << "solving ..." << std::endl;
	ans = solve(a, 0, n - 1);
	std::cout << "coin " << ans << " is fake" << std::endl;
	return 0;
}

int solve(std::vector<int>& a, int low, int high)
{
	int sum1, sum2, mid, ret_val;
	if (low == high)		return low;		// 只有一个硬币
	if (low == high - 1)					// 只有两个硬币
	{
		std::cout << "  weighing coin " << low << " and " << high << std::endl;
		if (a[low] < a[high])	ret_val = low;
		else					ret_val = high;
		std::cout << "    --> coin " << ret_val << " is lighter" << std::endl;
		return ret_val;
	}

	mid = (low + high) / 2;
	if ((high - low + 1) % 2 == 0)				// 硬币数量为偶数
	{
		sum1 = std::accumulate(a.begin() + low, a.begin() + mid + 1, 0);
		sum2 = std::accumulate(a.begin() + mid + 1, a.begin() + high + 1, 0);
		std::cout << "  weighing coin " << low << "-" << mid << " and " << mid + 1 << "-" << high << std::endl;
	}
	else									// 硬币数量为奇数
	{
		sum1 = std::accumulate(a.begin() + low, a.begin() + mid, 0);
		sum2 = std::accumulate(a.begin() + mid + 1, a.begin() + high + 1, 0);
		std::cout << "  weighing coin " << low << "-" << mid - 1 << " and " << mid + 1 << "-" << high << std::endl;

	}

	std::cout << "    sum1=" << sum1 << " , sum2=" << sum2 << std::endl;
	if (sum1 == sum2)
	{
		std::cout << "    --> equal" << std::endl;
		return mid;
	}
	else if (sum1 < sum2)
	{
		std::cout << "    --> the former is lighter" << std::endl;
		if ((high - low + 1) % 2 == 0)	return solve(a, low, mid);	// 偶数
		else						return solve(a, low, mid - 1);	// 奇数
	}
	else
	{
		std::cout << "    --> the latter is lighter" << std::endl;
		return solve(a, mid + 1, high);
	}
}

Use the bisection method to find the maximum value on both sides

#include<stdio.h>
void maxmin(int a, int b, int* min, int* max);
int array[9] = { 1,3,4,5,6,7,8,9,2 };
 int main() {

	int _max, _min;
	maxmin(0, 8, &_min, &_max);
	printf("MAX:%d, MIN:%d", _max, _min);
}

void maxmin(int a, int b, int* min, int* max) {
	int lmax, lmin, rmax, rmin;
	if (a == b) *min = *max = array[a];

	else if (a == b - 1) {
		if (array[a] < array[b]) {
			*min = array[a];
			*max = array[b];
		}
		else {
			*min = array[b];
			*max = array[a];
		}

	}
	else {
		int mid = (a + b) / 2;
		maxmin(a, mid, &lmin, &lmax);
		maxmin(mid + 1, b, &rmin, &rmax);
		if (lmin < rmin) *min = lmin;
		else *min = rmin;
		if (rmax < lmax) *max = lmax;
		else *max = rmax;

	}

}