The content of the explanation is via https://blog.csdn.net/jeryjeryjery/article/details/52829142?locationNum=4&fps=1 , it is well written, and I understand it after a long time.
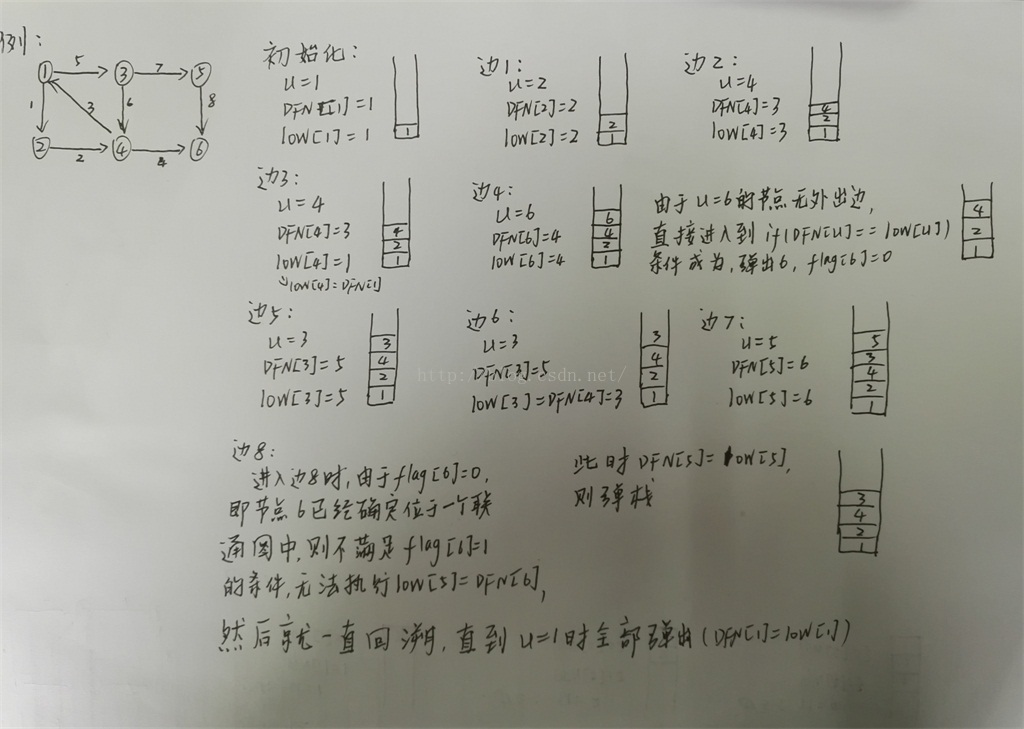
In a directed graph G, two vertices are said to be strongly connected if there is at least one path between them. A directed graph G is said to be strongly connected if every two vertices of it are strongly connected. The maximally strongly connected subgraph of a directed graph of a non-strongly connected graph is called a strongly connected component. As shown in the figure below, the strongly connected components are: {1, 2, 3, 4}, {5}, {6}
The Tarjan algorithm is an algorithm based on the depth-first search of the graph, and each strongly connected component is a child in the search tree Tree. When searching, the unprocessed nodes in the current search tree are added to a stack, and when backtracking, it can be determined whether the node from the top of the stack to the stack is a strongly connected component. Tarjan's algorithm is somewhat similar to the combination of postorder-based deep traversal search and union lookup, making full use of backtracking to solve problems.
The following variables are maintained for each node i in the Tarjan algorithm:
DFN[i] : The order in which node i is searched during depth-first search traversal.
low[i] : The earliest node in the stack that node i can go back to.
flag[i] : mark whether point i is on the stack.
The running process of Tarjan's algorithm:
(1). The first is to search all nodes in the graph in the order of depth-first search algorithm.
(2). During the search process, for any node u and the node v connected to it, different operations are performed according to whether the node v is in the stack:
*The node v is not in the stack, that is, the node v has not been visited, then continue to perform a deep search on v.
*Node v is already in the stack, that is, it has been visited, then determine the size of the DFN value of node v and the low value of node u to update the low value of node u. If node v's The DFN value is less than the low value of the node u. According to the definition of the low value (the earliest node that can be traced back to the stack), we need to update u with the DFN value. the low value of .
(3). In the backtracking process, for any node u, use its child node v (in fact, it cannot be regarded as a child node, but in the process of deep traversal, v is the node next to u after u) low value to update the low value of node u . Because node v can backtrack to a node that is already in the stack, node u must also be able to backtrack to it. Since there is a direct path from u to v, the node u that v can reach must also be reachable.
(4). For a connected graph, we can easily think that there is only one node u in the connected graph whose DFN value is equal to the low value . The node must be the first node visited in the connected graph in the process of deep traversal. Because its DFN value and low value are the smallest, it will not be affected by other nodes in the connected graph.
Below we demonstrate why only one node has equal DFN and low values. Assume that the DFN value and low value of two nodes are equal, because the DFN value of these two nodes must be different (The definition of the DFN value is the order in which it is accessed during deep traversal), so the two low values are definitely not equal. Since they are located in the same connected graph, the two nodes must be mutually reachable, so the low value of the two must be affected by the other (depending on whose low value is smaller), so it is impossible to have two pairs of DFN values and Nodes with equal low values.
Therefore, in the process of backtracking, we can judge whether a sub-connected graph has been found by judging whether the low value of the node is equal to the DFN value. Since the node whose DFN value is equal to the low value in the connected graph is the first node to be accessed in the connected graph, and according to the characteristics of the stack (the node pushed into the stack first is further inside the stack), then the node in the innermost. Therefore , all nodes in the connected graph can be popped by popping the stack continuously until the node with the same DFN value and low value is popped.
Next is my showtime:
To illustrate the algorithm idea in my words:
Oops....let me organize the language....
First of all, you need to know what the tarjan algorithm uses: dfn array (recording the order in which each point is pushed onto the stack, as a sequence number), low array (representing the minimum sequence number of the point that this point can go back to), stack (the first time The access should be pushed into the stack. If you judge that you are a strongly connected graph, it will pop out of the stack), vis array (judging whether you are in the stack or not).
The algorithm idea is actually, for example, a point. When you are visited for the first time, first assign your own dfn and low values, push the stack, assign the vis value to 1, and then look at the point you point to: if this point has never been accessed If you have visited, you should make this point recursive tarjan algorithm, so that you can compare with it, if its low value is small then you use its low value (because it can reach the smallest point you can also reach!); If this point has been visited and is still in the stack (still in the stack means that it has not been popped out of the stack as another connected graph (as in point 6 in the above figure)), then look at its dfn Is the value smaller than your low value? If so, it means that it is the smallest point you can currently reach. Update your low value quickly! (The relationship between point 3 and point 1 in the figure).
If the points you point to are done as above and the loop is over, then you should compare your dfn value == your low value. Because if you can be in a strongly connected component, and your dfn value is the smallest dfn value among the points you can reach, shouldn't the smallest point you can reach be yourself? So if it is true, it means that the hypothesis is true, and you are in a strong connected component.
Then according to the "first in, last out" of the stack, you must be under the stack now, then pop out of the stack, until you are out, then the strong connectivity component you are in has already been popped out of the stack. Note that vis is set to 0 when popping the stack, so that it does not affect the points of other connected graphs.
Example problem (the code is the tarjan algorithm template) :
Ideas :
It is to find the number of points of the smallest connected component! (Of course, a point does not count as a connected component)
AC code :
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
vector<int> v[maxn];
int dfn[maxn];
int low[maxn];
int cnt=0;
int vis[maxn]; //1 means in the stack
stack<int> s;
int minn=0x3f3f3f3f;
void tarjan(int a)
{
s.push(a);
force[a]=1;
dfn[a]=low[a]=++cnt;
for(int i=0;i<v[a].size();i++)
{
int e=v[a][i];
if(dfn[e]==0) //The point has not been visited yet
{
Tarjan (e);
low[a]=min(low[a],low[e]);
}
else if(vis[e]==1) //Visited and still on the stack
{
low[a]=min(low[a],dfn[e]);
}
}
if(dfn[a]==low[a]) //You belong to a strongly connected component
{
int ans=0; //Record the number of points in your strongly connected component
while(1)
{
int t=s.top();
s.pop();
force[t]=0;
years++;
if(t==a)
break;
}
if(ans!=1) //Because your own strong connection of a point does not meet the meaning of the question
from = min (from, ans);
}
}
intmain()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
int e;
scanf("%d",&e);
v[i].push_back(e);
}
tarjan(1);
cout<<minn;
return 0;
}