hdu2841 Visible Trees (Mobius inversion + number theory block)

Title:

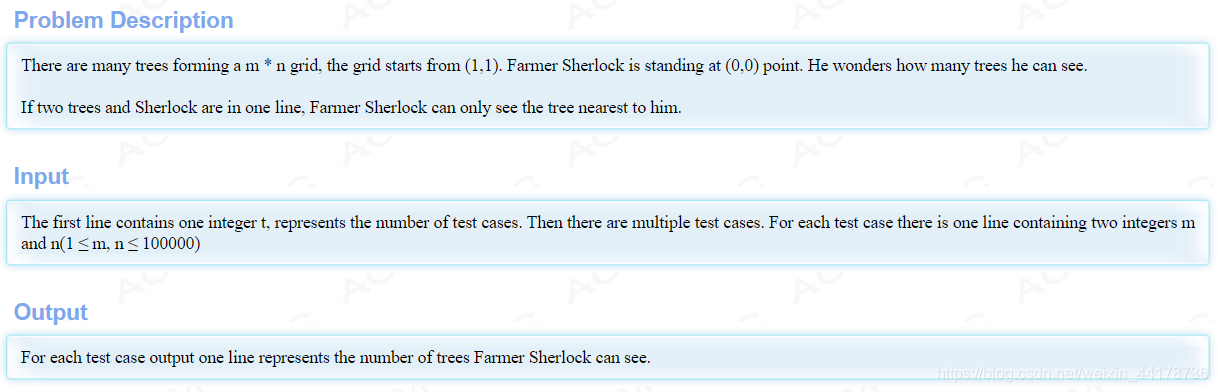
solution:

对于点(x,y),如果gcd(x,y)=1,那么这个点就能被看到,
否则这个点一定会被(x/gcd(x,y),y/gcd(x,y))挡住.

那么问题变为计算n*m的矩阵中,有多少个点横纵坐标互质.

$$\begin{gathered} ans=\sum _{i=1}^n\sum _{j=1}^m[gcd(i,j)=1] \\ Existinthe\; anti-playknottheory:\left[gcd\right(i,j)=1]=\sum _{d|gcd(i,j)}\mu \left(d\right) \\ Thatithas:ans=\sum _{i=1}^n\sum _{j=1}^m\sum _{d|gcd(i,j)}\mu \left(d\right) \\ Morechangepiecesmoveforwardorder,Firstgoldcited,Thatithas: \\ \sum _{d=1}^n\mu \left(d\right)\sum _{d|i,i<=n}\sum _{d|j,j<=m}1 \\ \sum _{i=1}^n\mu \left(d\right)\lfloor \frac{n}{d}\rfloor \lfloor \frac{m}{d}\rfloor \\ Thenplayanumber\; ofonsubblocksmay\; betooptimizationoftheO(\sqrt{n}) \end{gathered}$$

code：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxm=1e5+5;
int p[maxm],c;
int np[maxm];
int mu[maxm];
int n,m;
void init(){
    
    
    mu[1]=1;
    for(int i=2;i<maxm;i++){
    
    
        if(!np[i])p[c++]=i,mu[i]=-1;
        for(int j=0;j<c;j++){
    
    
            if(p[j]*i>=maxm)break;
            np[p[j]*i]=1;
            mu[p[j]*i]=i%p[j]?-mu[i]:0;
            if(i%p[j]==0)break;
        }
    }
    for(int i=1;i<maxm;i++){
    
    
        mu[i]+=mu[i-1];
    }
}
void solve(){
    
    
    cin>>n>>m;
    int mi=min(n,m);
    int ans=0;
    for(int l=1,r;l<=mi;l=r+1){
    
    
        r=min(n/(n/l),m/(m/l));
        ans+=(mu[r]-mu[l-1])*(n/l)*(m/l);
    }
    cout<<ans<<endl;
}
signed main(){
    
    
    init();
    int T;cin>>T;
    while(T--){
    
    
        solve();
    }
    return 0;
}

---