[LeetCode-Sword Finger Offer] 54. The k-th largest node of the binary search tree

1. Topic

Given a binary search tree, find the k-th largest node in it.

Example 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4

Example 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

limit:

1 ≤ k ≤ number of binary search tree elements

Two, solve

1. Recursion

Ideas:

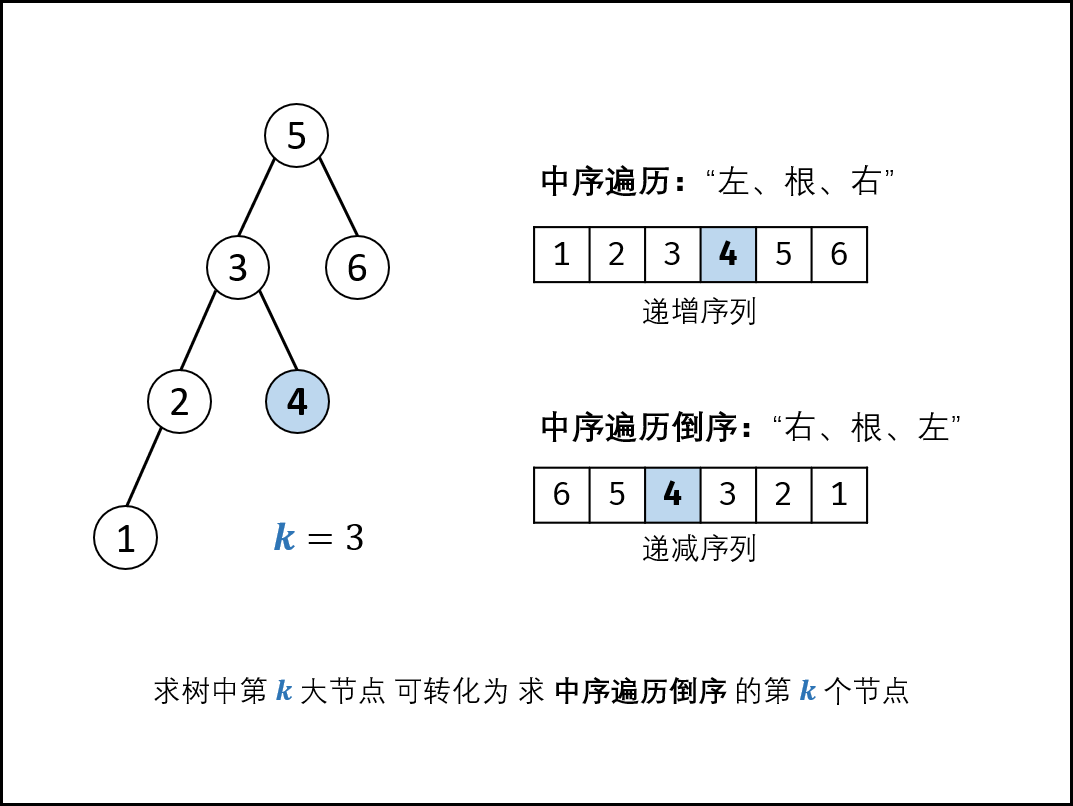
Nature : The middle order traversal of the binary search tree is an increasing sequence.

Corollary: the reverse order of the middle order traversal of the binary search tree is a descending sequence.
Therefore, finding the klargest node of the binary search tree can be transformed into finding the first knode in the reverse order of the middle-order traversal of this tree .

Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    
    int res, k;
    public int kthLargest(TreeNode root, int k) {
    
    
        this.k = k;
        dfs(root);
        return res;
    }
    void dfs(TreeNode root) {
    
    
        if(root == null) return;
        dfs(root.right);
        if(k == 0) return;
        if(--k == 0) res = root.val;
        dfs(root.left);
    }
}

Time complexity: $O (n)$
space complexity: $O (n)$

2. Iteration

Ideas:

Binary tree in-order traversal code template:

public List<Integer> inorderTraversal(TreeNode root) {
    
    
    List<Integer> result = new ArrayList<>();
    Deque<TreeNode> stack = new ArrayDeque<>();
    TreeNode p = root;
    while(!stack.isEmpty() || p != null) {
    
    
        if(p != null) {
    
    
            stack.push(p);
            p = p.left;
        } else {
    
    
            TreeNode node = stack.pop();
            result.add(node.val);  // Add after all left children
            p = node.right;   
        }
    }
    return result;
}

Modify the above template and change the original left-root-right traversal order to right-root-left .

Code:

class Solution {
    
    
    public int kthLargest(TreeNode root, int k) {
    
    
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode p = root;
        while(!stack.isEmpty() || p != null) {
    
    
            if(p != null) {
    
    
                stack.push(p);
                p = p.right;
            } else {
    
    
                TreeNode node = stack.pop();
                if (--k == 0) return node.val;
                p = node.left;   
            }
        }
        return 0;
    }
}

Time complexity: $O (n)$
space complexity: $O (1)$

Three, reference

1. Interview question 54. The k-th largest node of the binary search tree (in-order traversal + early return, clear illustration)