Article Directory
0 Notes
This blog post is a second compilation of the key notes of Li Yongle's basic course on behalf of the teacher in 2021. According to the teaching material used by Teacher Li, which is the catalog of the fifth edition of "Engineering Mathematics: Linear Algebra" of Tongji edition, I divide my notes into 6 sections, and I will try my best to put each note in the appropriate chapter. If you encounter complicated formulas, I will upload handwritten pictures or screenshots of textbook formulas instead of them because I haven't learned LaTeX (the phone camera may not take the pictures clearly, but I will try to make the content as complete as possible).
This note is not a systematic arrangement of the above-mentioned textbooks, and is only suitable for your future study and research.
1 Determinant
There are no special formulas to remember.
2 Matrix and its operation
1. Find A -1 B: Construct a matrix (A|B) and transform it into (E|X) through elementary transformation, and X is what you want.
2. Find AB -1 : Construct a matrix (B T |A T ) and transform it into (E|X) through elementary transformation, and X T is what you want.
3. If A is an n-order matrix, then ① r(A)<k⇔A's k-order sub-formula (if any) are all 0; ② r(A) ≥ k⇔A k-th order sub-formula exists or not 0; ③A≠0⇔r(A)≥1;④r(A)=n⇔|A|≠0⇔A is an invertible matrix; ⑤r(A)<n⇔|A|=0⇔A is not invertible;
4. A and B are n-order matrices. If A is invertible, then r(AB)=r(B), r(BA)=r(B).
5. A and B are n-order matrices, max{r(A),r(B)}≤r(A|B)≤r(A)+r(B).
6. Let A * be the adjoint matrix of the n-order matrix A, then: ① |A * |=|A| n-1 ; ② A -1 =A * /|A|; ③AA * =|A|E; ④|kA|=k n |A|.
7. A and B are m×n-order matrices. If there is an n-order invertible matrix P and an m-order invertible matrix Q, so that B=QAP, then A and B are called equivalent, denoted as A≌B.
8. A and B are matrices of order m×n, then A≌B⇔r(A)=r(B)⇔A can get B after a finite number of elementary transformations.
9. Let A * be the adjoint matrix of the n-order matrix A, there are: ① If r(A)=n, then r(A * )=n; ② If r(A)=n-1, then r(A * )=1; ③ If r(A)≤n-2, then r(A * )=0.
10 、 r (A T A) = r (A) = r (A T ) = r (AA T )。
3 Matrix elementary transformation and linear equations
1. For the n-variable linear equation system Ax=b, there are: ① no solution ⇔r(A)+1=r(A|b); ② unique solution ⇔r(A)=r(A|b)=n; ③ Infinitely many solutions ⇔ r(A)=r(A|b)<n.
2. For the n-variable homogeneous linear equations Ax=0, there are: ① there is a non-zero solution ⇔r(A)<n; ② there is only a zero solution ⇔r(A)=n.
3. The matrix equation AX=B has a solution ⇔r(A)=r(A|B).
4. If the number of equations in the equation system is less than the number of unknowns, the equation system must have non-zero solutions.
5. After a finite number of elementary row transformations, A gets B, then A≌B, and there must be an invertible matrix P, making PA=B. The column vectors of A and B: ① have the same linear correlation; ② have the same linear representation.
4 Linear correlation of vector groups
1. <α, β> is the vector product operation of vectors α and β, then <α, β> 2 =||α|| 2 ·||β|| 2 , the equal sign is and only if α and β are linearly related Established when.
2. In the three-dimensional vector space, let the coordinates of the vectors α and β under the same set of bases be (a 1 , a 2 , a 3 ) and (b 1 , b 2 , b 3 ) respectively, and let α and β be sandwiched between If the angle is θ, then:
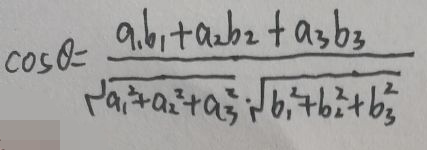
3. Let n-dimensional vectors α 1 ,α 2 ,...,α n be a set of pairwise orthogonal non-zero vectors, then α 1 ,α 2 ,...,α n are linearly independent vectors group.
4. The necessary and sufficient condition for vector group Ⅰ to be equivalent to vector group Ⅱ is that vector group Ⅰ and vector group Ⅱ can be expressed linearly with each other.
5. If vector group Ⅰ can be expressed linearly by vector group Ⅱ, then r (vector group Ⅰ) ≤ r (vector group Ⅱ); if vector group Ⅰ can be expressed linearly by vector group Ⅱ, and the number of vectors in vector group Ⅰ> The number of vectors in the vector group II, the vector group I must be linearly related; if the vector group I is linearly independent, and the vector group I can be expressed linearly by the vector group II, then the number of vectors in the vector group I ≤ the vectors in the vector group II number.
6. Vector group Ⅰ is equivalent to vector group Ⅱ ⇔ r (vector group Ⅰ) = r (vector group Ⅱ) = r (vector group Ⅰ, vector group Ⅱ).
7. n+1 n-dimensional vectors must be linearly related; if the vector group α 1 ,α 2 ,…,α s is linearly related, then α 1 ,α 2 ,…,α s ,…,α t must be linearly related; if The vector group I is irrelevant, and the high-dimensional vector group after expanding the dimension of each vector in the vector group I is still irrelevant.
8, a single vector [alpha] . 1 related ⇔α . 1 is a zero vector; two vectors [alpha] . 1 , [alpha] 2 associated ⇔α . 1 , [alpha] 2 collinear; three vectors [alpha] . 1 , [alpha] 2 , [alpha] . 3 related ⇔α . 1 , [alpha] 2 ,α 3 is coplanar.
9. If the vectors in the vector group Ⅰ are unit vectors, that is, the modulus length of each vector is 1, and the vectors are orthogonal to each other, that is, the inner product is 0, then the vector group Ⅰ is called an orthonormal group .
5 Similarity matrix and quadratic form
1. Let A be an n-th order matrix, α is an n-dimensional non-zero column vector, if A·α=λ·α, then λ is the eigenvalue of matrix A, and α is the eigenvector of matrix A corresponding to the eigenvalue λ .
2. Let A be an n-order matrix, then ① the trace of A tr(A)=Σλ i =Σa ii ; ② Πλ i =|A|. In this way, the eigenvalues of A reversible ⇔ A are non-zero.
3. The eigenvectors of different eigenvalues of matrix A are linearly independent. If A is a real symmetric matrix of order n, then the eigenvectors of different eigenvalues of A are pairwise orthogonal.
4. Assuming that both A and B are n-th order matrices, if there is an invertible matrix P such that P -1 AP=B, then A~B.
5. If A~B, then ① |λE-A|=|λE-B|, and the eigenvalues of A and B are exactly the same; ② r(A)=r(B); ③ |A|=|B| ;④ tr(A)=tr(B).
6. If the third-order matrix A can be similarly diagonalized into a matrix Λ, then the eigenvalues of A λ 1 , λ 2 , and λ 3 form a diagonal matrix Λ=diag(λ 1 ,λ 2 ,λ 3 ), corresponding to A The eigenvectors r 1 , r 2 , and r 3 of λ 1 , λ 2 , and λ 3 form an invertible matrix P=(r 1 , r 2 , r 3 ), and P -1 AP=Λ, that is, A~Λ.
7, if the third-order matrix A has three independent eigenvectors R & lt . 1 , R & lt 2 , R & lt . 3 , R & lt meet · A I = [lambda] I · R & lt I , I = l, 2,3. That is, A(r 1 ,r 2 ,r 3 )=(λ 1 ·r 1 ,λ 2 ·r 2 ,λ 3 ·r 3 )=(r 1 ,r 2 ,r 3 )·diag(λ 1 ,λ 2 ,λ 3 ), let P=(r 1 ,r 2 ,r 3 ), Λ=diag(λ 1 ,λ 2 ,λ 3), then AP=PΛ, that is, P -1 AP=Λ. In short, the n-order matrix A can be similarly diagonalized ⇔ A has n unrelated eigenvectors.
8. If the n-order matrix A has n different eigenvalues, then A must be similarly diagonalized; if λ is the k-fold eigenvalue of A, then λ corresponds to at most k unrelated eigenvectors; A can be similar diagonally If λ is the k-fold eigenvalue of matrix A, then λ corresponds to k independent eigenvectors.
9. If A is a real symmetric matrix of order n, then the eigenvalues of A are all real numbers.
10. A is any real symmetric matrix of order n, there must be an orthogonal matrix P of order n, so that P -1 AP=Λ=diag(λ 1 ,λ 2 ,...,λ n ).
11. The quadratic form and its matrix are expressed as follows. The rank of matrix A is the rank of the quadratic form:
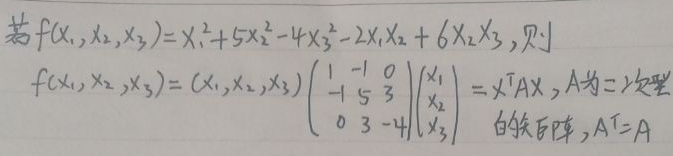
12. The standard form of the quadratic form has only square terms and no mixed terms:

13. The standard form of the quadratic form must first be the standard Type, that is, there is only a square term, no mixed term, and the coefficient of the second square term can only be -1,0,+1, such as:
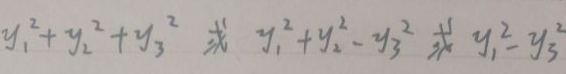
14. For the standard type, record the positive inertia index as p and the secondary inertia index as q. For the three quadratic forms in the above figure, they are [p=3,q=0], [p=2,q=1], and [p=1,q=1].
15. Quadratic transformation:

16. Contract: If C T AC = B, where C is reversible, then it is called the contract between A and B, which is recorded as A≃B.
17. Any quadratic form can be transformed into a standard form through coordinate transformation. There are two methods-matching method and orthogonal transformation method.
18. For any quadratic form f=x T Ax, where A T = A, there is always an orthogonal transformation x=Py, where P is an orthogonal matrix, making the quadratic form a standard form x T Ax=y T Λy=Σλ i ·y i 2 , where λ i is the n eigenvalues of A.
19. The canonical form of the quadratic form is unique (theorem of inertia): For any quadratic form x T Ax, the positive and negative inertia exponents are uniquely determined in the standard form transformed into a coordinate transformation.
20. Positive definite quadratic form: set quadratic form f(x)=x T Ax, if for any non-zero vector x=(x 1 ,x 2 ,…,x n ) T , there will always be f(x)>0 , Then f(x) is called positive definite quadratic form, and the corresponding matrix A is called positive definite matrix.
21. The quadratic form does not change its positive definiteness after coordinate transformation: under the coordinate transformation x=Cy, the quadratic form x T Ax has the same positive definiteness as the quadratic form y T C T ACy.
22. The necessary condition for quadratic positive definite is that all main diagonal elements a ii > 0. The necessary and sufficient conditions for quadratic positive definite: ① Quadratic f(x)=x T Ax positive definite; ② The square coefficients of the standard form of f(x) are all greater than 0; ③ Positive inertia index p=n; ④ A and E contract, that is, there is a reversible C, so that C T AC = E, A ≃ E; ⑤ A's eigenvalues are all greater than 0; ⑥ A's sequential principals and sub-forms are all greater than 0.
23. The necessary condition for the positive definite n-order real symmetric matrix A is |A|>0. The necessary and sufficient conditions for the positive definite n-order real symmetric matrix A: ① A and E contract, that is, there is an invertible C, such that C T AC = E, A ≃ E; ② A's positive inertia index is equal to n; Greater than 0; ④ The eigenvalues of A are greater than 0; ⑤ There is a reversible U, so that A=U T U.
24. Similarity matrices have the same eigenvalues, characteristic polynomials, determinants, ranks, and traces.
25. If A is an n-order matrix, let r different eigenvalues of A be λ 1 , λ 2 ,...,λ r , and the corresponding multiple root numbers are p 1 , p 2 ,..., p r , called P I is [lambda] I algebraic repeatability, [lambda] I dimensionality of feature space, i.e. corresponding to [lambda] I wherein the number of independent vectors is referred to as geometric repeatability.
26. The inverse of the λ matrix and the digital matrix (if invertible) are both: A -1 =A * /|A|.
27. The necessary and sufficient condition for any λ matrix to be invertible is that its determinant is a non-zero constant.
28. Let the rank of the λ matrix A(λ) be r: ① Determinant factor: For a positive integer 1≤k≤r, A(λ) must have a non-zero k-th order sub-formula, and all of A(λ) are non-zero The greatest common factor D k (λ) in which the first coefficient of the k-th order sub-formula is 1 is called the k-th order determinant factor of A(λ); ② The invariant factor of A(λ):
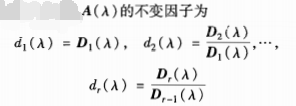
if the n-th order λ matrix A ([lambda]) of full rank, the [pi] d · C I ([lambda]) = | a ([lambda]) |, C is a nonzero constant, all D I number of ([lambda]) and a = n; ③ by elementary factors are not constant factor The invariant factor of 1 is divided into terms. The following is an example:

29. Assuming that both A and B are n-order digital matrices, the necessary and sufficient conditions for A to B are: ① λE-A≌λE-B; ② λE-A It has the same Schmidt standard form as λE-B; ③ λE-A and λE-B have the same constant factor; ④ λE-A and λE-B have the same determinant factor; ⑤ λE-A and λE- B has the same elementary factors.
30. For the digital matrix A, the invariant factor of λE-A is called the invariant factor of A, and the elementary factor of λE-A is called the elementary factor of A.
31, if A is an n-order matrix, the rank provided λE-A is the same factor r, λE-A is D I ([lambda]), I = R & lt .... 1. Then the Schmidt standard type of λE-A is:

6 Linear space and linear transformation
1. The vector group (α 1 , α 2 , α 3 ) and (β 1 , β 2 , β 3 ) are two different bases in the three-dimensional vector space, if (β 1 , β 2 , β 3 )=(α 1 ,α 2 ,α 3 )·P, then P is called the transition matrix from the vector group (α 1 ,α 2 ,α 3 ) to (β 1 ,β 2 ,β 3 ). P=(β 1 , β 2 , β 3 ) -1 · (α 1 , α 2 , α 3 ).
2. The matrices under different bases of the same linear transformation are similar, and similar matrices have the same eigenvalues, characteristic polynomials, determinants, ranks, and traces.
3, set V . 1 , V 2 is the linear space of the two sub-spaces V, if V . 1 ∩V 2 = {0} vector, called V . 1 and V 2 and a space V . 1 + V 2 is straight and, referred to as V 1 ⊕V 2 . The following propositions are equivalent: ① V 1 +V 2 is a direct sum; ② dim(V 1 +V 2 )=dim(V 1 )+dim(V 2 ); ③ If the vector group Ⅰ is a basis of V 1 , Vector group Ⅱ is a basis of V 2 , then {vector group Ⅰ, vector group Ⅱ} is a basis of V 1 +V 2 .
4. Let W be a subspace of V, and take α∈V. If there is α⊥β for any β∈W, then it is called α⊥W.
5. Pythagorean theorem: If both α and β are non-zero vectors, and α⊥β, then ||α+β||=||α-β||=||α|| 2 +||β| | 2 .
After I counted it, I realized that there were exactly 60 notes, haha!
END