
table of Contents

1 Overview
1.1 Retrospective thinking
Backtracking algorithm (Backtrack) is a kind of trial-and-error thought, which is essentially depth-first search . That is: starting from a certain state of the problem, try the choices that can be made in the existing state in turn to enter the next state. This process is recursive, if in a certain state no more choices can be made, or the target answer has been found, then take one step or even multiple steps to try again, until all choices have been tried in the end.
The whole process is like walking a maze. When we encounter a bifurcation, we can choose to go in from one direction and try. If you reach a dead end, return to the last fork and choose another direction to continue trying until you find that there is no exit, or you find an exit.
1.2 The three elements of backtracking
After understanding the idea of backtracking algorithm, let's analyze the key points of backtracking. In the backtracking algorithm, three elements need to be considered: path, selection list, and end condition . Take walking the maze as an example:

- 1. Path: Choices that have been made
- 2. Selection list: the choices that can be made in the current state
- 3. End condition: the selection list is empty, or the target is found
To get out of this maze, we need to repeat one thing: choose to go in from one direction and try. If you reach a dead end, return to the last fork and choose another direction to continue trying. Realized by program, this repetitive thing is a recursive function. In practice, we can follow a problem-solving template & idea:
fun backtrack(){
1\. 判断当前状态是否满足终止条件
if(终止条件){
return solution
}
2\. 否则遍历选择列表
for(选择 in 选择列表){
3\. 做出选择
solution.push(选择)
4\. 递归
backtrack()
5\. 回溯(撤销选择)
stack.pop(选择)
}
}
It should be noted that the problem-solving framework & ideas are not rigid, and should be analyzed in detail based on specific issues. For example, backtracking (revocation of selection) is not necessary. In Section 3.2, the k-th ordering and the number of islands in Section 5 , they do not need to be back-tracked after the deep function returns.
1.3 Retrospective pruning
Because the time complexity of the backtracking algorithm is very high, when we encounter a branch, if we "have the foresight" and know that a certain choice will not find the answer in the end, then we should not try to follow this path. This step is called Pruning .
So, how do you find this "foresight"? After my conclusion, there are probably the following situations:
- Duplicate state
For example: 47. Permutations II Full permutation II (using repeated numbers) This question is given a sequence that can contain repeated numbers, and requires all non-repetitive permutations to be returned. For example, the [1,1,2]expected output of input is [1,1,2]、[1,2,1]、[2,1,1]. Using the problem-solving template we introduced earlier, this problem is not difficult:

class Solution {
fun permute(nums: IntArray): List<List<Int>> {
val result = ArrayList<List<Int>>()
// 选择列表
val useds = BooleanArray(nums.size) { false }
// 路径
val track = LinkedList<Int>()
fun backtrack() {
// 终止条件
if (track.size == nums.size) {
result.add(ArrayList<Int>(track))
return
}
for ((index, used) in useds.withIndex()) {
if (!used) {
// 做出选择
track.push(nums[index])
useds[index] = true
backtrack()
// 回溯
track.pop()
useds[index] = false
}
}
}
backtrack()
return result
}
}
复制代码
However, because there are two 1s in the original array, there will be some repetitions in the result. How to remove the duplicates? One way is to check whether the same arrangement already exists in the result set after getting the arrangement. This is an O(n2)O(n^2)O(n2) comparison, which is obviously unwise. Another way is to look for repetitive states and avoid some choices "presciently" from the beginning.
Let's talk about what is the repetition state first? Remember the three elements of backtracking we talked about: path, selection list, and end condition . Generally speaking, the end conditions are fixed in these three elements, and the path and selection list will change with each selection & backtracking.
In other words, when we find that the paths and selection lists of the two states are exactly the same, it means that the two states are completely duplicated. The recursion starts with two repeated states, and the final result must be repeated. In this question, we first entered the implementation of quick sort , before each selection after first determine whether the current state and on a selected repeat, is the skip.
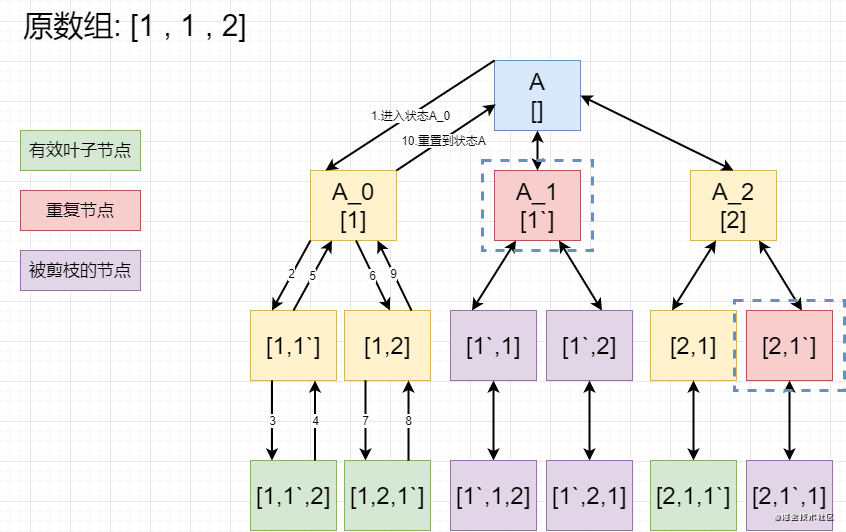
class Solution {
fun permuteUnique(nums: IntArray): List<List<Int>> {
val result = ArrayList<LinkedList<Int>>()
if(nums.size <= 0){
result.add(LinkedList<Int>())
return result
}
// 排序
Arrays.sort(nums)
// 选择列表
val used = BooleanArray(nums.size){false}
// 路径
val track = LinkedList<Int>()
fun backtrack(){
// 终止条件
if(track.size >= nums.size){
result.add(LinkedList<Int>(track))
return
}
for((index,num) in nums.withIndex()){
if(used[index]){
continue
}
if(index > 0 && !used[index - 1] && nums[index] == nums[index - 1]){
continue
}
// 做出选择
used[index] = true
track.push(num)
// 递归
backtrack()
// 回溯
used[index] = false
track.pop()
}
}
backtrack()
return result
}
}
- The final solution is determined
After we have determined the final solution in a selected branch, there is no need to try other options. For example, in 79. Word Search word search , when determining the existence of the word, there is no need to continue the search, and in Section 4 will be devoted to the analysis of this question.
fun backtrack(...){
for (选择 in 选择列表) {
1\. 做出选择
2\. 递归
val match = backtrack(...)
3\. 回溯
if (match) {
return true
}
}
}
- Invalid choice
When we can judge that a certain choice cannot find the final solution based on the known conditions, there is no need to try this choice. For example: 39. Combination Sum , 60. Permutation Sequence k permutation
3. Permutation & Combination & Subset Problem
3.1 Permutation & Combination Problem
**Permutation & combination & subset ** can be said to be the most common problem in backtracking algorithms. Among them, the subset problem is essentially a combination problem. Let's take you through a simple question experience permutation & combination of distinction:
- Arrangement problem:
There are 3 different balls A, B, C, and 2 of them are taken out and placed in a row. How many ways?
- Combination problem:
There are 3 different balls A, B, C, and 2 of them are taken out and put in a pile. How many ways?
What is the difference between a row and a pile? Obviously, one row is in order, while the other is unordered. For example, [ABC] and [ACB] are different, while {ABC} and {ACB} are the same.
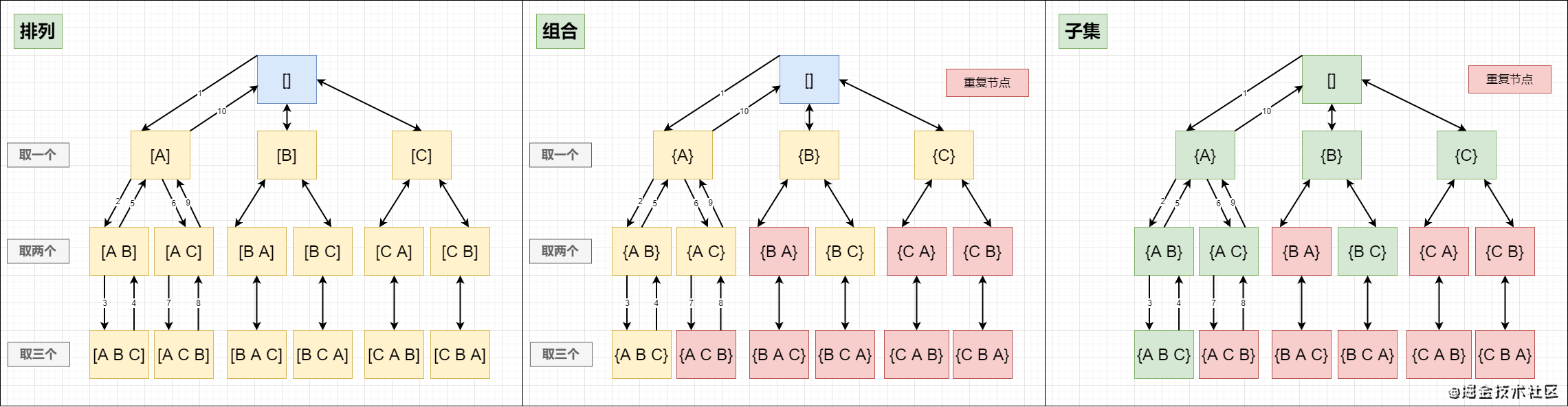
From the above picture, in fact, it can be clearly seen that the combination problem is to remove duplicate sets on the basis of the permutation problem; the subset problem is to merge multiple combination problems of different scales.
So, how to exclude collections with the same elements but different orders? Here is a very well-understood method. I believe that many students will come to realize once I say it: "This is how my junior high school math teacher taught me."

As you can see, as long as you avoid combining the previous elements, you can avoid duplication. For example, after selecting {B, }, do not combine the previous A elements, otherwise it will cause duplication. Because in the branch of {A, }, the combination of {A, B} already exists. Therefore, we can use a from variable to indicate the range of the select list allowed by the current state.
The following gives the permutation & combination code of taking k from n numbers. Since the recursive solution code is more interpretable, readers should first ensure that they can write recursive solutions proficiently:

Complexity analysis:

3.2 The problem of lexicographical arrangement
In the arrangement problem, there is also the concept of **Dictionary order**, which is based on alphabetical order, just like the order of words in a dictionary, for example [ABC] is arranged before [ACB] . To get the full permutation in lexicographic order, both recursive and non-recursive solutions can be implemented.
Recursive solution, you only need to ensure that the selection list in alphabetical order, the resulting whole arrangement is lexicographical sort is relatively straightforward to implement, in Section 1.4 has been given the answer.
The basic idea of using non-recursive solution is: starting from the current string, directly find the next arrangement in lexicographic order, for example, directly find the next arrangement [ACB] from [ABC]. How to find it, you can briefly consider this question first:
- Next permutation
31. Next Permutation Next Permutation Rearrange the given sequence of numbers into the next larger permutation in lexicographic order.

After understanding the algorithm for the next permutation, it is not difficult to write the algorithm for the full permutation. It only needs to output the next permutation from the first permutation, and finally get the full permutation in lexicographic order. If you are interested, you can check the solution in the previous section, and I won’t post it here.
- Kth permutation
In addition to finding the next permutation, it is also very common to find the kth permutation. For example: 60. Permutation Sequence the kth permutation , 440. K-th Smallest in Lexicographical Order K-th Smallest in Lexicographical Order . The basic idea is: by calculating the factorial, know the number of leaf nodes of this branch in advance, and pruning if k is not on this branch:
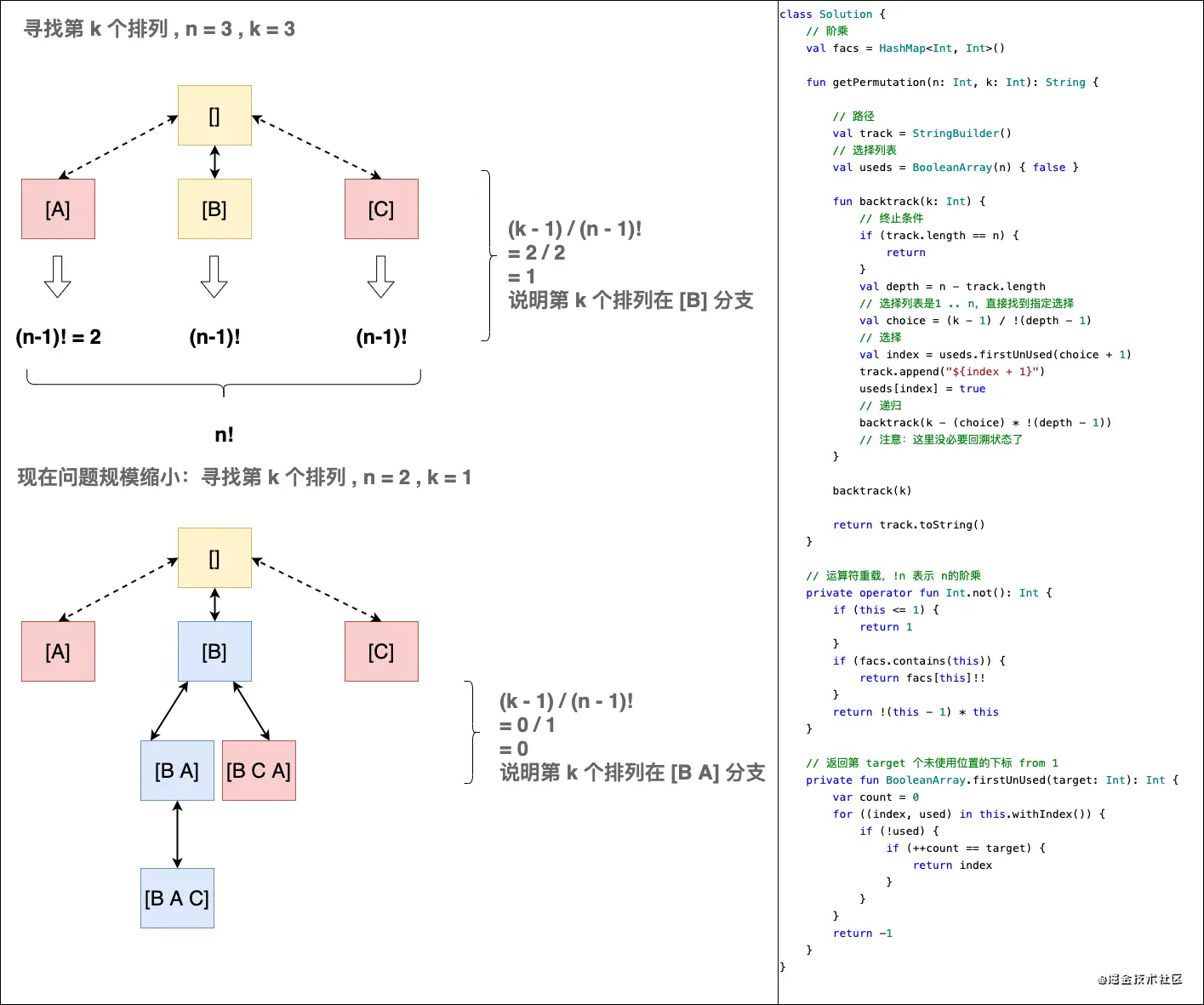
4. Two-dimensional plane search problem
The problem of walking the maze mentioned at the beginning of the article is actually a backtracking algorithm problem on a two-dimensional plane. The current position is the end point when the condition is terminated. Since it is a backtracking algorithm, there is no escape from the three elements that we have repeatedly emphasized: path & selection list & termination conditions:
4.1 Path-two-dimensional array useds
In the full permutation problem, we use a one-dimensional Boolean array used to mark the path that has been traversed. Similarly, in a two-dimensional plane, we need to use a two-dimensional Boolean array to mark the path that has been traversed.
1\. 一维数组 int[] useds
2\. 二维数组 int[][] useds
4.2 Selection List-Offset Array
When searching on a two-dimensional plane, the selection list of a point is its up, down, left, and right directions (except the direction of coming). For the convenience of coding, an offset array can be used, and the order of the 4 offsets in the offset array Is irrelevant
int[][] direction = {
{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
4.3 Check boundaries
Two-dimensional planes usually have boundaries, so you can write a function to determine whether the current input position is out of bounds:
private boolean check(int row, int column) {
return row >= 0 && row < m && column >= 0 && column < n;
}
With the previous foreshadowing, let's look at this question: 79. Word Search Word search is easier to understand.
5. Flood Fill problem
Flood Fill (Flood Fill, or Seed Fill) is an advanced version of the two-dimensional plane search problem in the previous section. That is: Find the connected nodes that meet the conditions on the two-dimensional plane .
The so-called connected nodes refer to two nodes connected in four directions: up, down, left, and right. Some questions will be extended to 8 directions (4 directions diagonally), but only a few more directions, there is no big difference. For example, the following image colorizes the white squares connected to the center nodes:

The whole problem-solving on a frame with the two-dimensional search problem much the same here that focused on another solution: disjoint-set , in this article, we have already been explained in detail and check usage scenarios and problem-solving skills set :"Data Structure Interview Questions | Union Search Set & Union-Search Algorithm"
Simply put: Union search set is suitable for dealing with the connectivity problem of disjoint sets , which is suitable for solving the connectivity problem of Flood Fill. We can merge the nodes connected to the central node into the same component. After all the processing is completed, we can judge whether the two nodes are connected by querying and collecting:
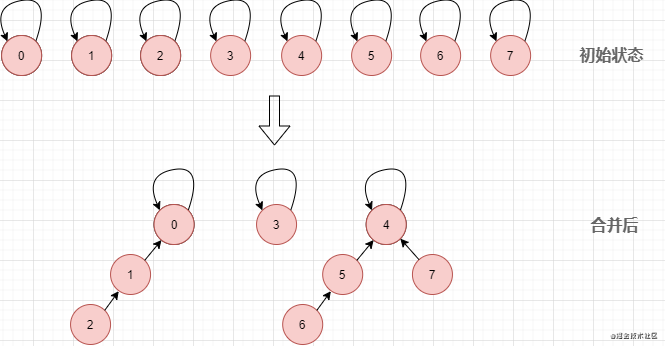
Tip: Using path compression and merging by rank at the same time, the time complexity of the query is close to O(1)O(1)O(1)
6. Summary
The idea of backtracking algorithm is not complicated, but it is indeed a high-frequency test site; proficient in backtracking algorithm is also very helpful for understanding dynamic programming algorithm, and the learning priority is higher.
This article has been included in the open source project: https://github.com/xieyuliang/Note-Android , which contains self-learning programming routes in different directions, interview question collection/face sutras, and a series of technical articles, etc. The resources are continuously being updated...
Share it here this time, see you in the next article .
Reference
- "Backtracking" -Wikipedia
- "Flood Fill" -Wikipedia
- "Entry-level detailed explanation of backtracking algorithm + exercises (all arrangement I)" -by liweiwei
- "Backtracking Search + Pruning (All Arrangement II)" by liweiwei
- "Using Backtracking on a Two-dimensional Plane (Word Search I)" by liweiwei
- "Backtracking Algorithm" -by liweiwei
- "Detailed Explanation of Backtracking Algorithms" -by labuladong
- "Detailed Explanation and Application of FloodFill Algorithm" -by labuladong
- "The Beauty of Data Structures and Algorithms" -by Wang Zheng, produced by GeekTime
- "300 Minutes to Get an Algorithm Interview" —— Likou & Lagou.com
Author: Peng ugly
original address: https: //juejin.cn/post/6882928981268496398