1. Dijikstra algorithm theory
In a weighted graph, from a single source node to other nodes, how to find the shortest path among all paths is the shortest path problem of unit nodes. In the routing algorithm, similar to this, the model can be abstracted. Dijkstra's algorithm was proposed in 1959 by Dutch computer scientist Dijkstra. It is the shortest path algorithm from one vertex to the other vertices, which solves the shortest path problem in a directed graph. The main feature of Dijkstra's algorithm is that the starting point is the center and the outer layer is expanded until it reaches the end point.
ØBasic idea
When calculating the shortest path in graph G through Dijkstra, you need to specify the starting point s (that is, starting from the vertex s). In addition, two sets S and U are introduced. The function of S is to record the vertex of the shortest path (and the corresponding shortest path length), while U is to record the vertex of the shortest path (and the distance from the vertex to the starting point s). Initially, there is only the starting point s in S; U is the vertex other than s, and the path of the vertex in U is "the path from the starting point s to the vertex". Then, find the vertex with the shortest path from U and add it to S; then, update the vertex in U and the path corresponding to the vertex. Then, find the vertex with the shortest path from U and add it to S; then, update the vertex in U and the path corresponding to the vertex. … Repeat this operation until all vertices have been traversed.
ØOperation steps
\1. Initially, S only contains the starting point s; U contains other vertices except s, and the distance of the vertex in U is "the distance from the starting point s to the vertex" [For example, the distance of the vertex v in U is (s ,v), then s and v are not adjacent, then the distance of v is ∞].
\2. Select the "shortest distance vertex k" from U, and add vertex k to S; at the same time, remove vertex k from U.
\3. Update the distance from each vertex in U to the starting point s. The reason why the distance of the vertex in U is updated is that k is the vertex of the shortest path determined in the previous step, so that k can be used to update the distance of other vertices; for example, the distance of (s, v) may be greater than (s, k)+(k,v) distance.
\4. Repeat steps (2) and (3) until all vertices are traversed.
Ø illustration
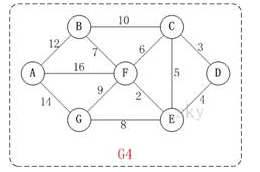
The above figure G4 is taken as an example to demonstrate Dijkstra's algorithm (take the 4th vertex D as the starting point). In the following node B, 23 should be 13.
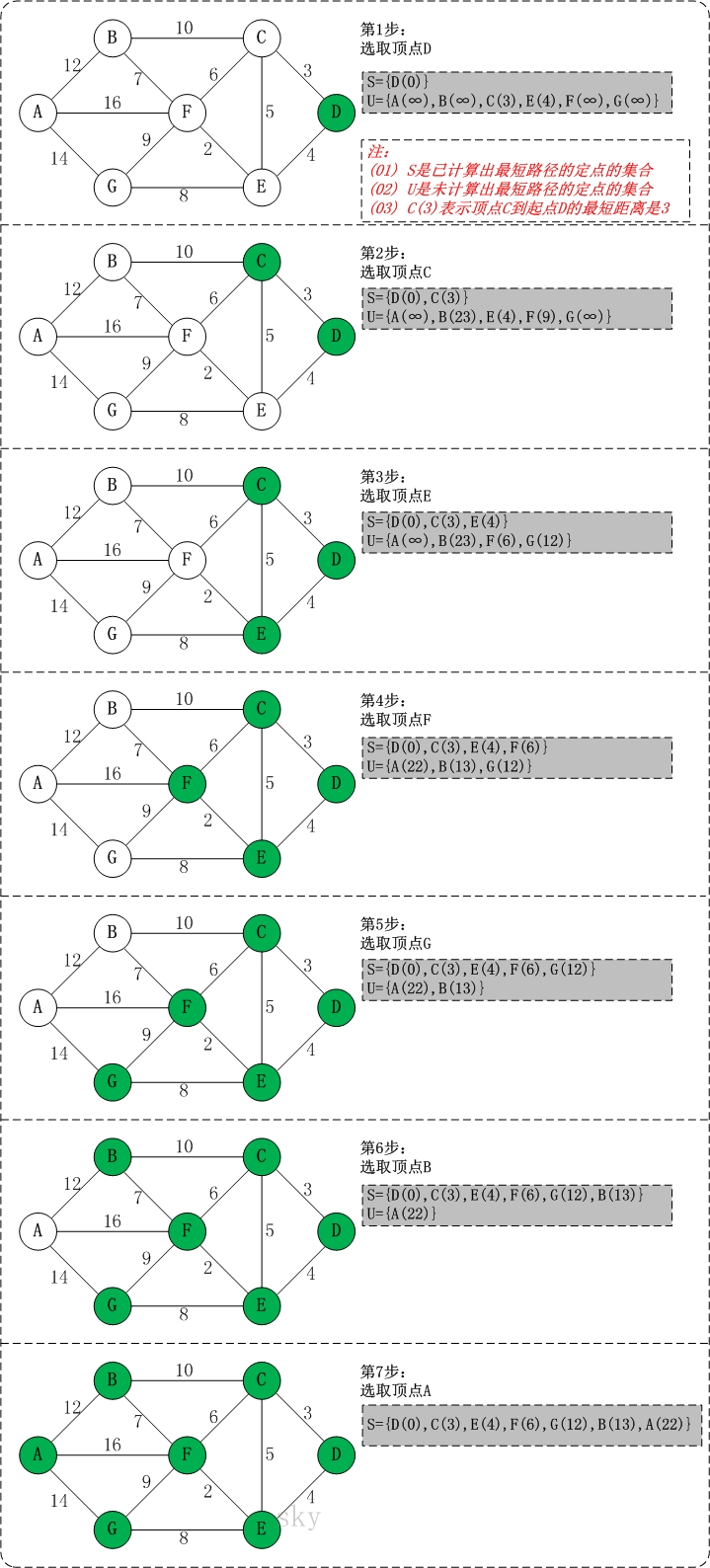
Initial state: S is the set of vertices whose shortest path has been calculated, and U is the set of vertices whose shortest path has not been calculated!
Step 1: Add vertex D to S.
At this time, S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}. Note: C(3) means that the distance from C to the starting point D is 3.
Step 2: Add vertex C to S.
After the previous operation, the distance between the vertex C in U and the starting point D is the shortest; therefore, add C to S and update the distance of the vertex in U at the same time. Taking vertex F as an example, the distance from F to D before is ∞; but after adding C to S, the distance from F to D is 9=(F,C)+(C,D).
At this time, S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}.
Step 3: Add vertex E to S.
After the previous operation, the distance between the vertex E in U and the starting point D is the shortest; therefore, E is added to S, and the distance of the vertex in U is updated at the same time. Taking vertex F as an example, the distance from F to D was 9 before; but after adding E to S, the distance from F to D is 6=(F,E)+(E,D).
At this time, S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}.
Step 4: Add vertex F to S.
At this time, S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}.
Step 5: Add vertex G to S.
At this time, S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}.
Step 6: Add vertex B to S.
At this time, S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}.
Step 7: Add vertex A to S.
At this time, S={D(0), C(3), E(4), F(6), G(12), B(13), A(22)}.
At this time, the shortest distance from the starting point D to each vertex is calculated: A(22) B(13) C(3) D(0) E(4) F(6) G(12).
2 . Golang Dijikstra algorithm to achieve
func Dijkstra_Alg(D [LEN][LEN]int, v int) {
if v < 0 || v >= LEN{
fmt.Println("错误节点输入!")
return
}
//替换一些原数组中的-1
for i:=0; i<LEN; i++ {
for j:=0; j<LEN; j++ {
if D[i][j] == -1{
D[i][j] = 9999999
}
}
}
//1. 创建S集合
S := make([]int, 0)
S = append(S, v)
//2. 对于当前顶点,做一次迪杰斯特拉算法
//看邻接表对应的那一列
for {
//2.1 找出当前列最小加入到S, 要排除掉已经在S中的点
min := 9999999
index := v
for i:=0; i<LEN; i++{
if !Contains(S, i) && D[i][v] < min{
min = D[i][v]
index = i
}
}
//填充之前判断一下,防止后面都是无穷大
if min == 9999999 && index == v{
break //如果最小的都是∞那么说明后面没有点可以加入了,所以结束
}
fmt.Printf("最小值min=%d, 加入节点%d \n", min, index)
S = append(S, index) //加入目前最小的到S中
//2.2 根据先加入的这个点,更新其他点的权重
for i:=0; i<LEN; i++ {
if !Contains(S, i) && D[i][index] + min < D[i][v]{
D[i][v] = D[i][index] + min
}
}
fmt.Println("集合S:", S)
//2.3 检测下S是否满了,满了就退出,不满就重复前两步
if len(S) >= LEN{
break
}
fmt.Println("===============================")
}
//输出数组看一下
fmt.Println("-----------------Dijkstra算法结果-----------------")
fmt.Println(S)
fmt.Println("-----------------最短路径:-----------------")
fmt.Printf("点%d到各个点的最短路长度是:\n", v)
for i:=0; i<len(S); i++ {
fmt.Printf("(%d, %d) = %d \n", v, S[i], D[S[i]][v])
}
}
Program test run results:

3. Floyd algorithm theory
The Floyd algorithm is also known as the interpolation method, which is an algorithm used to find the shortest path between multiple sources in a given weighted graph. The name of the algorithm is named after Robert Freud, one of the founders, winner of the Turing Award in 1978, and Professor of Computer Science at Stanford University.
Find the shortest path matrix between every two points of a graph through the weight matrix. Starting from the weighted adjacency matrix A=[a(i,j)] n×n of the graph, recursively update n times, that is, from the matrix D(0)=A, according to a formula, construct the matrix D(1) ; Use the same formula to construct D(2) from D(1);...; Finally, use the same formula to construct a matrix D(n) from D(n-1). The element in row i and column j of matrix D(n) is the shortest path length from vertex i to vertex j. D(n) is called the distance matrix of the graph. At the same time, a subsequent node matrix path can be introduced to record the distance between two points. The shortest path. The relaxation technique (relaxation operation) is used to perform a relaxation on all other points between i and j. So the time complexity is O(n^3).
The core idea is to select a node as an intermediate transition node each time through a triple nested loop, and determine between any other two pairs of nodes. If the selected node is used to transition and the path length obtained is shorter, then the pair is updated. The path distance between nodes, that is, the value of the distance matrix corresponding to the update, so that the outermost loop controls the selected node as the update node, and the two nested loops select any two nodes as traversals. To judge whether the distance obtained by transitioning through the selected intermediate node is shorter, so that the outermost loop, each time the next step is performed, the distance proof will be updated, that is, the corresponding matrix update change in the Warshall method.
Advantages: easy to understand, the shortest distance between any two nodes can be calculated, and the code is simple to write.
Disadvantages: The time complexity is relatively high, and it is not suitable for calculating large amounts of data.
4. Floyd algorithm Go programming implementation
func Floyd_Alg(D [LEN][LEN]int) {
//1. 创建对应的Path矩阵
//1.1 输出原邻接矩阵
fmt.Println("--------------------原来的邻接矩阵--------------------")
PrintMatrix(D[:])
//1.2 创建Path数组
var Path [LEN][LEN]int
for i:=0; i<LEN; i++ {
for j:=0; j<LEN; j++ {
Path[i][j] = -1
}
}
//2. 处理下原邻接矩阵的-1,不影响下面的判断
for i:=0; i<LEN; i++ {
for j:=0; j<LEN; j++ {
if D[i][j] == -1{
D[i][j] = 9999999
}
}
}
//3. 三层循环更新原邻接矩阵和Path矩阵
for v:=0; v<LEN; v++ {
for i:=0; i<LEN; i++ {
for j:=0; j<LEN; j++ {
//制造全排列
if i == j || v == j || v == i{
//三者不能相等,相等则跳过
continue
}
//fmt.Printf("V:%d, (%d, %d)\n", v, i, j)
//如果加上中间点,可以减小距离,那么就更新两个表
if D[i][j] > D[i][v] + D[v][j] {
D[i][j] = D[i][v] + D[v][j] //更新原邻接矩阵
Path[i][j] = v //更新Path路径图
}
}
}
}
//4. 输出邻接矩阵和没两个点之间的最短路径
fmt.Println("--------------------Floyd求得的最短距离邻接矩阵--------------------")
PrintMatrix(D[:])
fmt.Println("-----------------------------------------------------------------")
fmt.Println(D)
//输出每两个点的最短路径
for i:=0; i<LEN; i++ {
for j:=0; j<LEN; j++ {
if i == j {
continue
}
fmt.Printf("(%d, %d)点%d到点%d的最短路径是:", i, j, i, j)
PrintPathMatrix(Path[:], i, j)
fmt.Printf("\n")
}
}
}
Screenshot of running result:

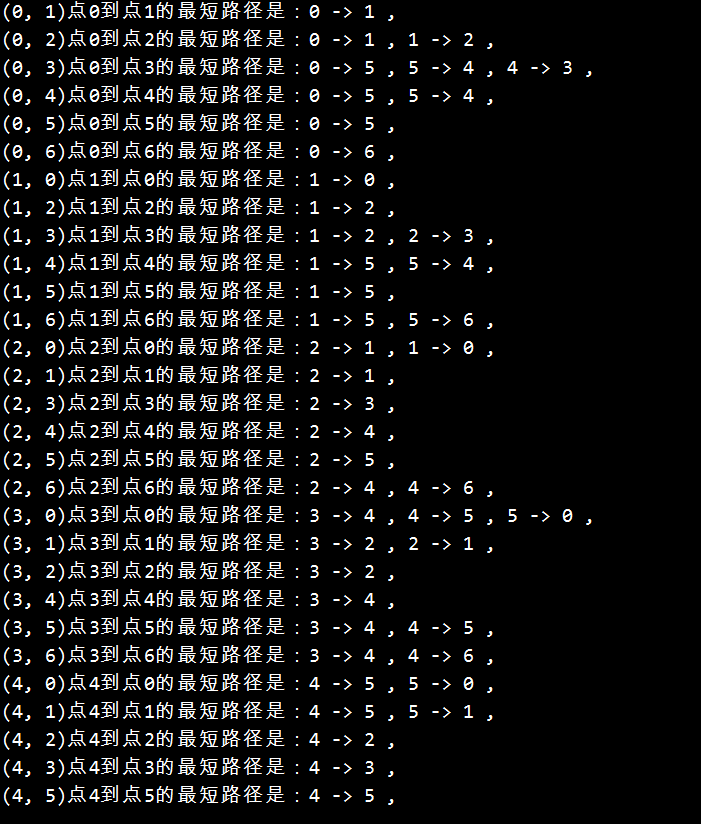
5. Summary of shortest path algorithm
The time complexity of the two methods is the third power of N, which is not suitable for the calculation of large amounts of data. In comparison, the ideas of Dijkstra's algorithm and Floyd's algorithm are both "greedy" ideas, while the shortest path output of Floyd's algorithm The idea of recursion is used. The Dijkstra algorithm can only find the shortest path from a single point to other points at a time, while the Floyd algorithm can find the shortest path between each point at one time. The above are the similarities and differences between the two algorithms.
Reference
CSDN:
https://blog.csdn.net/heroacool/article/details/51014824
https://www.cnblogs.com/skywang12345/p/3711512.html
https://blog.csdn.net/wang_dong001/article/details/50196103