Change 2 is another variant of the typical knapsack problem. We have already talked about the classic dynamic programming in the previous article : the 0-1 knapsack problem and the knapsack problem variant: equal subset division .
I hope you have read the first two articles and read the dynamic programming and the knapsack problem routine. This article will continue to follow the knapsack problem routine and list a variant of the knapsack problem.
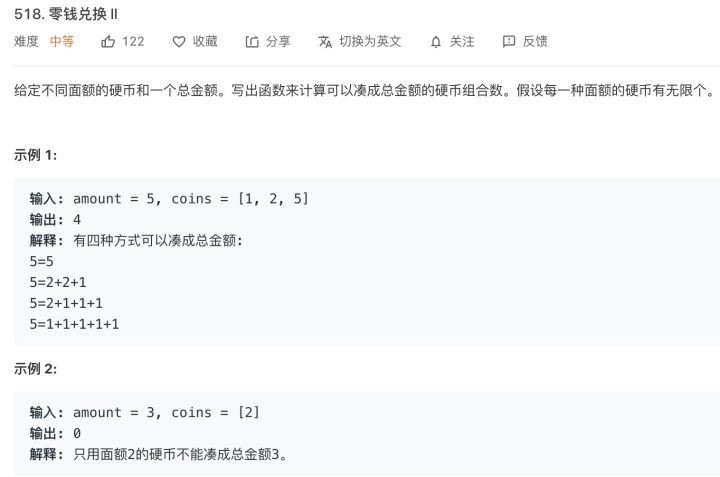
This article is about LeetCode question 518, Coin Change 2, and the title is as follows:
int change(int amount, int[] coins);
PS: As for Coin Change 1, we have written about the dynamic planning routine in our previous article .
We can turn this problem into a description form of the knapsack problem :
A backpack, the maximum capacity amount, a series of articles coins, the weight of each item coins[i], an unlimited number of each item . How many ways are there to fill the backpack exactly?
The biggest difference between this problem and the two knapsack problems we talked about earlier is that the number of each item is infinite. This is the legendary " complete knapsack problem ". There is a slight change in the transfer equation.
The following describes the form of the backpack problem, continue to analyze according to the process.
Problem solving ideas
The first step is to clarify two points, "status" and "choice" .
There are two states, namely "the capacity of the backpack" and "selectable items". The choice is "pack in the backpack" or "not in the backpack". The routine of the backpack problem is the same.
Understand the status and choice, the dynamic programming problem is basically solved, as long as you apply this framework to it:
All values of for state 1 in state 1: All values of for state 2 in state 2: for ... dp[state1][state2][...] = calculation (choose 1, choose 2...)
The second step is to clarify dpthe definition of the array .
First look at the "status" we just found, there are two, which means we need a two-dimensional dparray.
dp[i][j]The definition is as follows:
If only the former itwo items, when the capacity of the backpack jwhen there are dp[i][j]ways to fill the backpack.
In other words, the translation back to our title means:
If only coinsthe front iface value of the coin, if you want Couchu amount j, there are dp[i][j]kinds of error method .
After the above definition, we can get:
The base case is dp[0][..] = 0, dp[..][0] = 1. Because if you don't use any coin face value, you can't make up any amount; if the target amount made is 0, then "rule by doing nothing" is the only way to make up.
The answer we ultimately want to get is dp[N][amount], where Nis coinsthe size of the array.
The general pseudo-code idea is as follows:
int dp[N+1][amount+1] dp[0][..] = 0 dp[..][0] = 1 for i in [1..N]: for j in [1..amount]: Put item i into the backpack, Do not pack item i into the backpack return dp[N][amount]
The third step is to think about the logic of state transition based on "choice" .
Note that the special point of our problem is that the number of items is unlimited, so this is different from the backpack problem article written before.
If you don't ipack this first item into the backpack , that is to say you don't use coins[i]coins of this denomination, then jthe number of ways to make up the denomination dp[i][j]should be equal to the dp[i-1][j]previous result.
If you put this first iitem in the backpack , that is to say, you use coins[i]coins of this denomination, it dp[i][j]should be equal to dp[i][j-coins[i-1]].
First, since iit starts from 1, coinsthe index is the denomination of i-1the ifirst coin.
dp[i][j-coins[i-1]]It is not difficult to understand that if you decide to use this coin, then you should pay attention to how to collect the amount j - coins[i-1].
For example, if you want to use a coin with a face value of 2 to make up an amount of 5, then if you know how to make up an amount of 3 and add a coin with a face value of 2, then you can make up for 5.
PS: I have written more than 100 original articles carefully , and I have hand-in-hand brushed with 200 buckle questions, all of which are published in labuladong's algorithm cheat sheet , which is continuously updated . It is recommended to collect, brush the questions in the order of my articles , master various algorithm routines, and then cast them into the sea of questions.
In summary, there are two choices, and what we want to find dp[i][j]is "how many ways to do it together", so dp[i][j]the value should be the sum of the results of the above two choices :
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= amount; j++) {
if (j - coins[i-1] >= 0)
dp[i][j] = dp[i - 1][j]
+ dp[i][j-coins[i-1]];
return dp[N][W]
The last step is to translate the pseudo-code into code and handle some boundary conditions .
I wrote the code in Java, completely translated the above ideas, and dealt with some boundary issues:
int change(int amount, int[] coins) {
int n = coins.length;
int[][] dp = amount int[n + 1][amount + 1];
// base case
for (int i = 0; i <= n; i++)
dp[i][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= amount; j++)
if (j - coins[i-1] >= 0)
dp[i][j] = dp[i - 1][j]
+ dp[i][j - coins[i-1]];
else
dp[i][j] = dp[i - 1][j];
}
return dp[n][amount];
}
Moreover, we can discover through observation, dptransfer the array and only dp[i][..]and dp[i-1][..]are, therefore can be compressed state, further reducing the space complexity of the algorithm:
int change(int amount, int[] coins) {
int n = coins.length;
int[] dp = new int[amount + 1];
dp[0] = 1; // base case
for (int i = 0; i < n; i++)
for (int j = 1; j <= amount; j++)
if (j - coins[i] >= 0)
dp[j] = dp[j] + dp[j-coins[i]];
return dp[amount];
}
This solution is exactly the same as the previous idea, dpcompressing a two-dimensional array into one dimension, with a time complexity of O(N*amount) and a space complexity of O(amount).
So far, this change exchange problem has also been solved through the framework of the backpack problem.