目录


今天我们来讲一讲回溯中一个典型的专题 -- floodfill,也就是洪水灌溉问题
今天我们将用 7 道题目来带各位深度了解一下这个算法
(下文中的标题都是leedcode对应题目的链接)
733.图像渲染
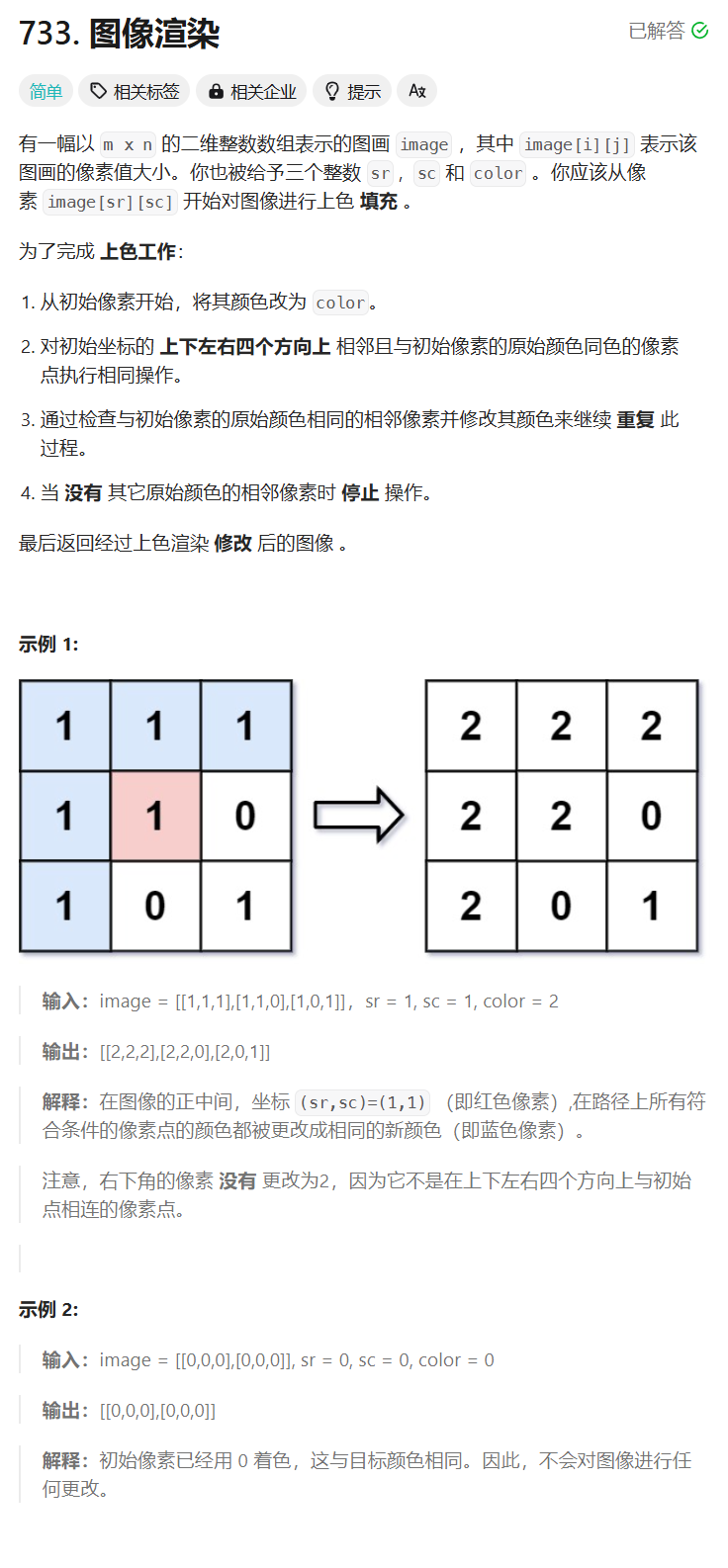
题意很简单,就是给你一个初始坐标,将所有和这个坐标对应值相同的位置全部改成另一个值而已
在正式开始做题目之前,我们需要先开辟两个数组表示上下左右的移动:
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
最后我们就直接从这个位置开始,分别对上下左右进行递归即可
不过需要注意的是,我们还有递归到原来位置的情况进而变成死递归,所以我们还需要一个check数组(bool类型),用来标记某个位置是否已经遍历过了
最后就是每遍历到一个位置,就将这个位置的值改变成color即可
带吗如下:
class Solution {
public:
int col, n, m, cmp;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<int>>& image, int i, int j)
{
image[i][j] = col;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && image[x][y] == cmp)
dfs(image, x, y);
}
}
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color)
{
col = color, n = image.size(), m = image[0].size(), cmp = image[sr][sc];
if(image[sr][sc] == color) return image;
dfs(image, sr, sc);
return image;
}
};200.岛屿数量

这道题目其实也是相当简单的,本质还是进入二维数组里面,上下左右地递归
但是现在要我们计算岛屿的数量,这样,我们可以在外面创建一个 bool 类型的 check 数组,接着我们就只需要在主函数遍历这个 grid 数组,当我们遇到 1 的时候,就代表我们碰到岛屿了,我们就进入递归的逻辑,如果遇到 0,就直接跳过
但是我们进入岛屿递归逻辑之后,我们还需要将对应位置的check数组打上标记,代表这个地方我们已经遍历过了,这一整块岛屿我们找过一遍了
所以主函数里面就是,当我们碰到 1 并且这个位置在 check 数组里面是false也就是没遍历过的话,我们就进入递归逻辑,而其他情况就都跳过即可
最后我们每进入一次递归逻辑,外面计数器就++一次,最后返回计数器即可
代码如下:
class Solution {
public:
int n, m;
bool check[301][301];
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<char>>& grid, int i, int j)
{
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] == '1' && !check[x][y])
{
check[x][y] = true;
dfs(grid, x, y);
}
}
}
int numIslands(vector<vector<char>>& grid)
{
int ret = 0;
n = grid.size(), m = grid[0].size();
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
{
if(grid[i][j] == '1' && !check[i][j])
{
ret++;
check[i][j] = true;
dfs(grid, i, j);
}
}
return ret;
}
};695.岛屿的最大面积

由于是求最大面积,所以我们需要在全局位置创建一个变量 ret,用来判断最大的面积(也就是每遍历完一个面积,我们就和 ret 比较一下)
最后就是,我们求的是一整块,不是一条道走到尾的情况,如下:

这一块的最右边那一列,我们可以往上走,也可以往下走,但我们是需要将这些全部加起来的,所以我们正确的作坊应该是,全局创建一个变量计算面积,每遍历到一个地方我们就++这个变量即可,最后和 ret 比较
最后我们在进入下一次的递归逻辑之前,还需要将这个变量重新置为 1,因为进入递归的地方也要算一个面积
代码如下:
class Solution {
public:
int n, m, ret, ps;
bool check[51][51];
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<int>>& grid, int i, int j)
{
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] == 1 && !check[x][y])
{
ps++;
check[x][y] = true;
dfs(grid, x, y);
}
}
}
int maxAreaOfIsland(vector<vector<int>>& grid)
{
ret = 0, ps = 0;
n = grid.size(), m = grid[0].size();
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
{
if(grid[i][j] == 1 && !check[i][j])
{
ps = 1;
check[i][j] = true;
dfs(grid, i, j);
ret = max(ps, ret);
}
}
return ret;
}
};130.被围绕的区域

这道题目,就是换一个思路的事情,因为求的是被包围的区域,所以我们可以先将那些没有被包围的区域打上标记,也就是从上下左右四条边开始出发,接着就是递归
最后那些没有递归到的位置,要么是海水要么是被包围的区域,我们就直接for循环嵌套遍历整张表,遇到 1 就改为 0 即可
代码如下:
class Solution {
public:
int n, m;
bool check[201][201];
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<char>>& board, int i, int j)
{
check[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && board[x][y] == 'O' && !check[x][y])
dfs(board, x, y);
}
}
void solve(vector<vector<char>>& board)
{
n = board.size(), m = board[0].size();
for(int i = 0; i < n; i++)
{
if(board[i][0] == 'O' && !check[i][0])
dfs(board, i, 0);
if(board[i][m-1] == 'O' && !check[i][m-1])
dfs(board, i, m-1);
}
for(int j = 0; j < m; j++)
{
if(board[0][j] == 'O' && !check[0][j])
dfs(board, 0, j);
if(board[n-1][j] == 'O' && !check[n-1][j])
dfs(board, n-1, j);
}
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
if(board[i][j] == 'O' && !check[i][j])
board[i][j] = 'X';
}
};417.太平洋大西洋水流问题

简单翻译一下题目,就是如果当前格子旁边有格子比他小或者等于的话,那么我们就可以走向下一个位置
然后题目要我们找出能够同时走到大西洋和太平洋的格子
其实这道题目正着解的话是很困难的,所以我们就需要正难则反,也就是,我们从上和左,以及左和下出发,就不断递归,然后我们设置两个数组,标记我们从大西洋或者太平洋出发能够走到的所有位置
最后我们直接遍历整个表格,如果有一个格子,从太平洋出发和大西洋出发都能走到的话,那就意味着这个点就是我们要找的点,直接记录当前节点即可
最后我们返回所有的符合条件的节点,代码如下:
class Solution {
public:
int n, m;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
bool pa[201][201], at[201][201];
void dfs(vector<vector<int>>& heights, int i, int j, bool flag)
{
if(flag) pa[i][j] = true;
else at[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && heights[x][y] >= heights[i][j])
{
if(flag && !pa[x][y])
dfs(heights, x, y, flag);
else if(!flag && !at[x][y])
dfs(heights, x, y, flag);
}
}
}
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights)
{
vector<vector<int>> ret;
n = heights.size(), m = heights[0].size();
// pa -- true
// at -- false
for(int i = 0; i < n; i++)
{
dfs(heights, i, 0, true);
dfs(heights, i, m-1, false);
}
for(int j = 0; j < m; j++)
{
dfs(heights, 0, j, true);
dfs(heights, n-1, j, false);
}
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
{
if(pa[i][j] == true && at[i][j] == true)
ret.push_back({i, j});
}
return ret;
}
};529.扫雷游戏

其实也是给你一个起点,然后我们从这个起点开始递归展开
但是我们还需要判断一下特殊情况,也就是,如果这个位置直接就是雷,那么我们改完当前位置之后直接返回即可
其他的情况我们就直接进入递归逻辑,进入之后我们还需要判断一下,我们当前位置四周是否有雷,也就是这个位置是空格还是数字
其实我们专门写一个函数,用来做判断四周有多少个雷的工作即可
如果是空格,那就是 0 个雷,我们就直接改完然后继续递归下去即可
如果有数字,那我们就只能改成数字,但是我们不能继续递归下去了,游戏规则就是这样的
代码如下:
class Solution {
public:
int n, m;
bool check[51][51];
int dx[8] = {0, 0, 1, -1, -1, 1, -1, 1};
int dy[8] = {1, -1, 0, 0, -1, -1, 1, 1};
char sta(vector<vector<char>>& board, int i ,int j)
{
int ret = 0;
for(int k = 0; k < 8; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && board[x][y] == 'M') ret++;
}
return ret + '0';
}
void dfs(vector<vector<char>>& board, int i, int j)
{
check[i][j] = true;
char set = sta(board, i, j);
if(set == '0') board[i][j] = 'B';
else
{
board[i][j] = set;
return;
}
for(int k = 0; k < 8; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && !check[x][y] && board[x][y] != 'M')
dfs(board, x, y);
}
}
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click)
{
n = board.size(), m = board[0].size();
int i = click[0], j = click[1];
if(board[i][j] == 'M')
{
board[i][j] = 'X';
return board;
}
dfs(board, i, j);
return board;
}
};LCR 130.衣橱整理
这一道题力扣翻译有点问题,我们看下面这张图,是剑指offer原题


其实这道题目知道题意之后相当简单,就是,我们每遍历到一个位置,就将两个下标分析一下,看看分开后加起来有没有超过cnt即可
接着就是,我们每到一个地方,就将计数器++,接着在进行递归逻辑之前,我们都先看一看,下标是否可行,如果可以,就直接递归,不行就不进入递归逻辑
而我们判断下标的工作可以专门写一个小函数来实现,这样子代码稍微优雅一点
代码如下:
class Solution {
public:
int m, n, tar, ret;
int dx[2] = {0, 1};
int dy[2] = {1, 0};
bool check[101][101];
bool comp(int i, int j)
{
int sum = 0;
string si = to_string(i);
string sj = to_string(j);
for(auto e : si) sum += e - '0';
for(auto x : sj) sum += x - '0';
return sum <= tar;
}
void dfs(int i, int j)
{
check[i][j] = true;
ret++;
for(int k = 0; k < 2; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !check[x][y])
{
if(comp(x, y))
dfs(x, y);
}
}
}
int wardrobeFinishing(int _m, int _n, int cnt)
{
m = _m, n = _n, tar = cnt, ret = 0;
dfs(0, 0);
return ret;
}
};结语
这篇文章到这里就结束了!!~( ̄▽ ̄)~*
如果觉得对你有帮助的,可以多多关注一下喔