目录

前言
在图中一共有两类算法,一种是最短路径,还有一种就是本篇要讲解的最小生成树算法了
其中,最短路径一共有三种,而最小生成树一共有两种,也就是克鲁斯卡尔(Kruskal)和普利姆算法(Prim)
至于最短路径算法,我们会在下一篇进行讲解
同时需要注意的是,下面的两种算法我们都会用邻接矩阵进行代码书写!!!(绝对不是因为他的代码比较好写)
同时,我们下面还会一直用到边,所以我们需要额外写一个类来表示边,如下:
struct Edge
{
size_t _srci;
size_t _dsti;
W _w;
Edge(size_t src, size_t dst, const W& w)
:_srci(src)
,_dsti(dst)
,_w(w)
{}
bool operator>(const Edge& e) const
{
return _w > e._w;
}
};什么是最小生成树算法
首先我们可以举一个例子帮忙理解,你,是一个城市路线规划师,现在要建各个地区之间的铁路,问你怎么样修铁路,怎么规划路线才能用最小的利益将所有城市链接起来
每一个城市之间都有相应的边的权重,有可能从 A 到 B 之间有一座大山,直接过去要挖隧道,但是从 C 绕过去的话就会便宜很多
而我们的图本质上就是边和节点构成的,我们每一条边都有相应的权重,最小生成树问的就是,如何让所有节点都连起来并且利益最大化
这时我们就有两个算法可以选择了,一个叫做克鲁斯卡尔,还有一个叫做普利姆,这两个都是人名,也就是这两个大佬发明出来的
而这两个算法本质上都是用的贪心算法,也就是每一次都直接选最小的边,只不过各自的思考方式是不一样的,这也就导致了两个算法各有特色,虽然都是贪心
Kruskal 克鲁斯卡尔
我们的克鲁斯卡尔算法,其实理解起来相当简单,就是在一开始的时候,我们就将所有边都放在小堆(priority_queue)里面,这样我们堆顶存的就是最小的边,然后我们每一次拿出来目前最小的边,一次一次地往图上放边即可
但是但是,这样会面临一个特别严重的问题就是,我们的图一共有 n 个节点(假设),那就意味着如果是最小生成树的情况的话,就必定有且仅有 n-1 条边,因为这样刚好将所有点链接起来
但是如果我们只是一味的往图里面放当前权重最小的边的话,就一定会出现本来两个节点已经链接起来了,但是我们当前权重最小的边又将这两个节点再链接一次的情况,如下:
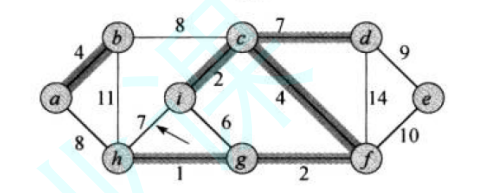
我们会看到,其中点 i 和点 h 已经链接起来了,也就是走的 i->c->f->g->h 这条路,但是当前权重最小的边是 i->h,但是我们是不能选择这条边的,因为本来这两个点就链接起来了,我们最小生成树要的只是全部节点链接起来的同时利益最大化,而不是单纯某两个点之间的利益最大化,如果要单纯两个点的话,那就是我们下一篇要讲的知识点了,也就是最短路径问题
但是接下来又有新的问题了,我们该如何辨认,某两个点之间,是否已经链接起来了呢?
其实这也非常简单,我们在学习图论之前,我们就学过了一个数据结构,叫做并查集
如果我们每一次遍历到一个新节点的时候,我就看看并查集里面,起始节点和当前节点是否是同一个根,这样就能判断这个节点是否已经链接过了
比如上面的,我们一共有两个并查集,假设我们第二个并查集的根就是 d,那么无论是 i 还是 h,他们的根都是 d,所以我们就能判断了,最后我们每加完一条新的边,就将结束节点放进并查集里面
至此,我们的克鲁斯卡尔算法的逻辑就讲完了,单纯的文字可能不太好理解,所以图示如下:

最后代码如下:
W kruskal(Self& minTree)
{
// 前期准备工作
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (auto& e : minTree._matrix)
{
e.resize(n, MAX_W);
}
//将所有的边都放进小堆里面
priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i < j && _matrix[i][j] != MAX_W)
minque.push(Edge(i, j, _matrix[i][j]));
int size = 0;
W total = W();
// 这个是并查集
UnionFindSet ufs(n);
//克鲁斯卡尔算法主逻辑
while (!minque.empty())
{
//每次取出堆顶,也就是权重最小的边
Edge min = minque.top();
minque.pop();
// 判断是否在同一个并查集里面
if (ufs.FindRoot(min._srci) != ufs.FindRoot(min._dsti))
{
minTree.AddEdge(min._srci, min._dsti, min._w);
ufs.Union(min._srci, min._dsti);
size++;
total += min._w;
}
}
if (size == n - 1) return total;
else return W();
}Prim 普利姆
看完了上面的 kruskal 算法之后,我们会发现他的思想其实就是纯贪,然后面对成环问题再想办法进行特判
但是我们的 Prim 算法的思想就不一样,他是不需要特判是否成环的
在普利姆的算法思想中,他将所有的点抽象成了两个集合,一个是已经确定了的,也就是已经选过了的点,另一个集合就是还没有选过的点的集合
然后我们会从一个起点出发,每一次我们都去看与这个点链接的其他点,也就是当前点的所有边,然后选取权重最小的那一条,如下:

在这张图里面,我们的起点是 a,然后我们第一次看的时候,就只会关注两条边,a->b 和 a->h,然后选择权重更小的 ab 边,最后将点 b 放进集合里面,已经选过了的点的集合
但是随着我们选边的进行,我们到后面就不是单对一个点进行判断,比如上面,我们选完 b 之后,我们接下来是对 bc、bh、ah 这三条边进行判断,也就是当前选了的边的集合往外扩展的所有边的最小值
同时,我们每一次选择的时候,我们都先看看选过了的集合里面是否有当前点,或者没选过的集合里面有没有当前点,判断出这个点没选过之后,我们再选取与这条边链接的所有的边里面权重最小的边
但是我们还有一个问题就是,第一个,我们怎么选出与当前边相连的边,第二个,怎么选出当前所有选过的边相连的边里面权重最小的边
其实两个问题都很好解决,第一个,由于我们用的是邻接矩阵,所以我们直接遍历起点的那一行即可,比如从 a 位置开始,我们就遍历 ab、ac、ad......但是还需要判断一下,如果邻接矩阵里面记录的当前位置的值为 INT_MAX的话,就代表这条边不存在
接着是第二个问题,我们只需要用一个小堆即可,如下:

我们每一次选的时候,所有选过的节点对应的边都被放进小堆里面了,我们只需要进行取堆顶并且判断权重最小的边的结束位置的节点是否已经被选过即可
至此,我们的 Prim 算法逻辑就全部讲完了,主要思路图示如下:

代码如下:
W Prim(Self& minTree, const V& src)
{
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (auto& e : minTree)
{
e.resize(n, MAX_W);
}
size_t srci = _indexMap[src];
priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
set<size_t> inSet;
inSet.insert(srci);
for (int i = 0; i < n; i++)
if (_matrix[srci][i] != MAX_W)
pq.push(Edge(srci, i, _matrix[srci][i]));
W total = W();
while (!pq.empty() && inSet.size() < n)
{
Edge min = pq.top();
pq.pop();
if (inSet.find(min.srci) == inSet.end() || inSet.find(min.dsti) == inSet.end())
{
minTree.AddEdge(min._srci, min._dsti, min._w);
total += min._w;
for (int i = 0; i < n; i++)
{
if (_matrix[min._dsti][i] != MAX_W && inSet.find(i) == inSet.end())
pq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
}
inSet.insert(min._dsti);
}
}
if (inSet.size() == n) return total;
else return W();
}结语
这篇文章到这里就结束啦!!~( ̄▽ ̄)~*
如果觉得对你有帮助的,可以多多关注一下喔