目录

前言
本篇博客将会讲解图论中的最短路径问题
这个问题一共有三种对应算法,一个是迪杰斯特拉(Dijkstra),这个是效率最高,最为热门,最受欢迎的算法,如果条件满足的话,那么用这个算法的效率无疑是最高的
但是这个算法有一个致命的缺点,就是如果我们有边的权重是负数的话,那么这个算法就算不出来最短路径了
所以我们就有了第二个算法,也就是贝尔曼-福特算法(Bellman-Ford),这个算法的本质就是,暴力将所有路径都枚举一遍,然后不断更新,直到我们更新出所有情况的最短路径,从某种意义上来讲,这个算法最坏的情况是O(n^3)的,但是很多时候并不用更新到那么多次,也就是O(n^2)到 O(n^3)之间
然而,上面两种算法都是帮助我们判断,以某一个点为起点的情况下,我们到达其他点的最短路径问题,也就是单源最短路径,单源的源代表的是源头的意思
但如果我们要知道从每一个点开始到达其他点的最短路径问题,也就是多源最短路径问题的话,我们就需要用到最后一个算法了,也就是弗洛伊德算法(Floyd-Warshall)
这个算法本质上是动态规划,我们会额外创建一张二维的 dp 表,最后将所有的结果都放在 dp 表上面,这个算法的效率同样不算高,但是他和贝尔曼福特算法一样,都可以处理权重包含负数的情况
而论代码书写的话,除了迪杰斯特拉之外,剩下两个的代码都超级好写,因为贝尔曼福特算法本质是暴搜,而动态规划的本质也是暴搜,只不过是将某个位置结果记录下来之后的暴搜而已
最后再来讲一讲什么是最短路径,我们可以举一个现实生活中的例子
比如你要去旅游,从你家开始出发,但是到达别的城市都有一定的消耗,也就是花钱
可能你要去哈尔滨玩,但如果是直达的话,可能要2500块(假设),但可能你从你家开始出发,先去北京然后再转到哈尔滨去,可能只用花2000块,那么第二种方法对比第一种直达的方法就是相对短的路径
而我们的最短路径问题就是这样的,每条边的权重都有一定的意义
比如你去每一个地方做生意,你去到了 A 城可以赚 1w,这时你的边的权重就是 1w
但如果你从 A 到 B 做完生意之后发现会亏 2w,那么此时边的权重就是 -2w,是负数
而上文也讲过了,如果带有负权重的边,我们只能用后两种算法,反之用迪杰斯特拉就是效率最高的
Dijkstra 迪杰斯特拉
首先我们需要知道的是,这是一个单源最短路径算法,所以我们一定会有一个起点
而我们这个算法其实只用一个vertor数组,数组里面每一个位置代表的都是,从起点出发到达这个点的最短路径距离
而迪杰斯特拉算法的核心一共就两步:
第一步:
我们从某个位置出发,将所有和他相连的边全部拿出来比较一遍,接着选权重最小的那个边。这其实也是一种贪心,就相当于我们每次都固定了一个点,每一次都能找到从起点出发到达这个点的最短路径
第二步:(松弛调节)
每固定一个新的点,我们就会去更新从这个点到与这个点相连的其他点的最短路径,如果我们发现经过这个点的话,到达另一个点的距离更短,我们就会将最短路径的距离更新(对于那个点而言)
看图就懂了,如下:

如上图,我们最开始是以 s 为起点,我们最开始没得找最短,因为第一次只能 s 到 s,也就是距离为 0,所以 s 点对应的距离就是 0,接着就是松弛调节,s 点对应的是点 t、y,所以更新两个的距离,一个是10,一个是 5
接着是第二次,我们已经固定了 s 点了,接着就是去找除了 s 点以外所有还没固定且已经松弛调节过了的点,上图中符合条件的点就是 t、y,而其中 y 点的距离更小,所以我们第二次固定的就是 y 点,接着是松弛调节,(c图)与 y 点相连的节点有三个,我们更新一下经过 y 点出发到其他点的距离即可
这样做的意义在于,比如上图我们从 s 直接到 t,最短是 10,但是从 s 出发,经过 y 然后再到 t 的最短距离是 8
最后处理两个细节问题,第一个是,我们怎么找出没有固定的点中已经松弛调节过了的点的最小值
第二个问题就是,我们怎么进行松弛调节
先来回答第一个:我们首先可以创建一个标记数组,当我们固定了一个点之后,我们就在标记数组中标记一下表示这个数已经被选过了,接着我们每一个点都会被放在另一个数组中,我们直接对这个数组进行遍历即可,如果这个位置的数没有被标记过的话,那么值就应该是INT_MAX,反之则是调整过,最后判断一下是否被标记数组标记过即可
接着是第二个问题:由于我们用的是邻接矩阵,所以我们遍历一下就可以了,然后判断松弛调节后的结果是否小于原先位置的值即可
综上就是我们迪杰斯特拉算法的全部了,文字看起来可能会较为繁琐,图示如下:

代码如下:
void Dijkstra(const V& src, vector<W>& dist)
{
size_t n = _vertexs.size();
size_t srci = _indexMap[src];
dist.resize(n, MAX_W);
dist[srci] = 0;
vector<bool> s(n, false);
for (int i = 0; i < n; i++)
{
W min = MAX_W;
int dst = 0;
for (int j = 0; j < n; j++)
{
if (s[j] == false && dist[j] < min)
{
min = dist[j];
dst = j;
}
}
s[dst] = true;
for (int k = 0; k < n; k++)
{
if (_matrix[dst][k] != MAX_W && !s[k]
&& dist[dst] + _matrix[dst][k] < dist[k])
{
dist[k] = dist[dst] + _matrix[dst][k];
}
}
}
}Bellman-Ford 贝尔曼福特算法
对于 Dijkstra 算法没法处理权值带负数的情况这里就不做详细说明了,只当一个结论,因为本篇博客最主要的还是介绍三个算法
接下来是贝尔曼福特算法,纯暴搜
其实这里面的每一次都相当于我们在迪杰斯特拉算法里面的松弛调节,固定一个点,然后列举所有的情况,不断进行松弛调节即可
但是但是,这种纯暴搜的方法,我们能只遍历一次吗?
我们来看下面这张图:
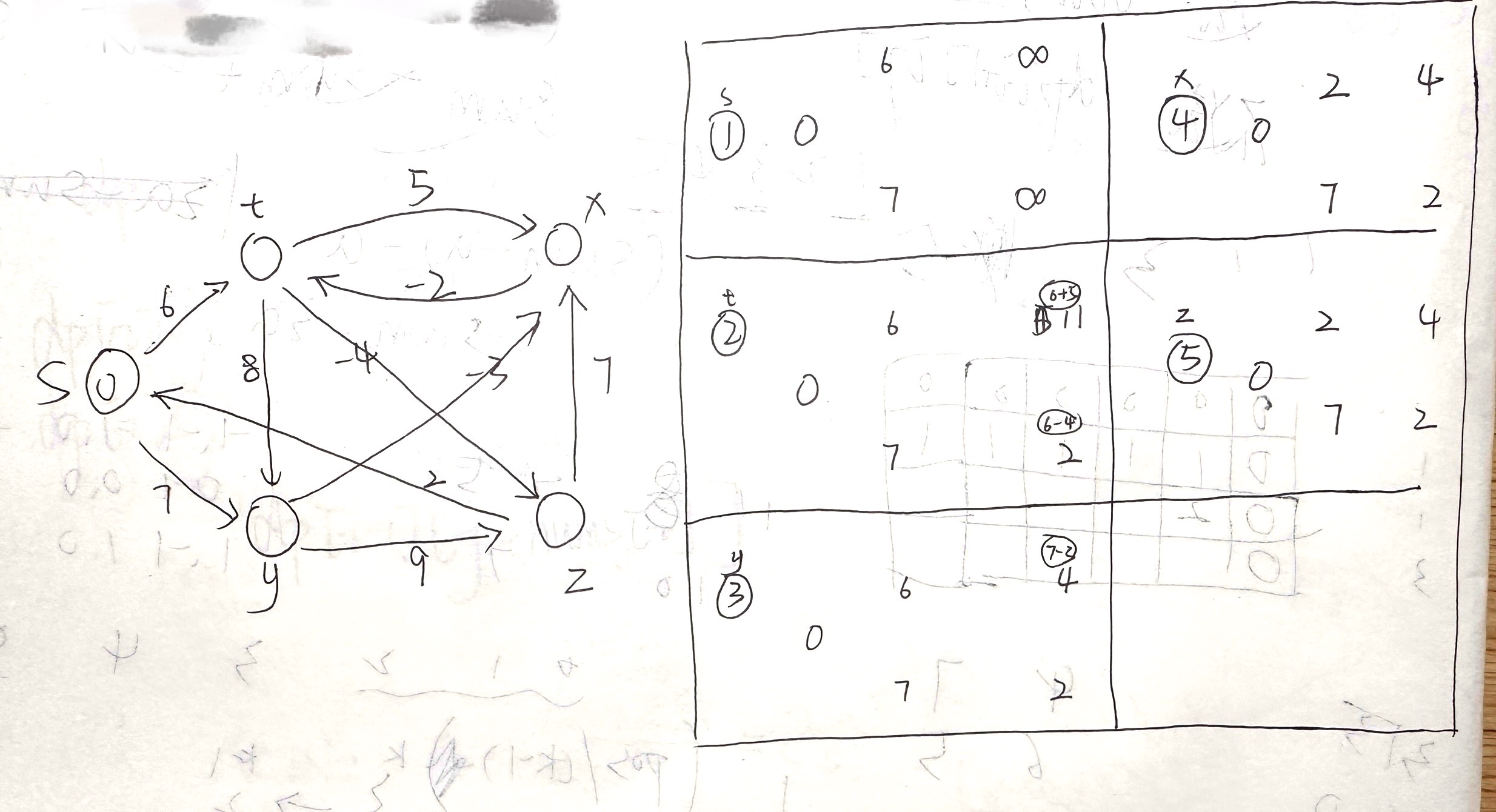
我们每一次都固定一个点,然后进行松弛调节,最后得出的结果就在步骤 5 里面
但是我们来看一看答案:

我们会发现,最右下角也就是点 z 应该是 -2 才对,但是我们的出来的结果确是 2,这是为什么呢?
首先我们要知道我们的 2 是怎么来的,这是我们固定了点 t 的时候,当时 t 是 6,然后 t->z 的边权重为 -4,6-4=2 得来的
但是当我们固定点 x 的时候,我们的点 t 被更新了,更新成了 2,但是我们此时已经没有办法再更新点 z 了,所以最终的结果自然就是 2 了,但如果我们再更新一次的话,其实最终的结果就出来了
但如果遇到更复杂的情况的话,我们再更新一次可能并不够,所以我们最保险的方法就是直接再更新 n 次(n 为节点总数量)
但是如果每一次都更新 n 次的话并没有必要,可是不更新 n 次的话又不保险,所以我们可以加一个判断,也就是定义一个 bool 类型的变量,当我们将所有节点都遍历了一遍之后,我们并没有进行任何的更新,那就意味着此时已经是最好的结果了,直接退出循环即可
代码也很好写,就是三层循环,第一层里面加一个判断,然后内部也是只有一个判断,仅此而已
代码如下:
bool BellmanFord(const V& src, vector<W>& dist)
{
size_t n = _vertexs.size();
size_t srci = _indexMap[src];
// vector<W> dist,记录srci-其他顶点最短路径权值数组
dist.resize(n, MAX_W);
// 先更新srci->srci为缺省值
dist[srci] = W();
// 总体最多更新n轮
for (size_t k = 0; k < n; ++k)
{
// i->j 更新松弛
bool update = false;
cout << "更新第:" << k << "轮" << endl;
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
// srci -> i + i ->j
if (_matrix[i][j] != MAX_W && dist[i] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
{
update = true;
dist[j] = dist[i] + _matrix[i][j];
}
}
}
// 如果这个轮次中没有更新出更短路径,那么后续轮次就不需要再走了
if (update == false)
{
break;
}
}
return true;
}但是我们还需要注意的一个小情况就是,负权回路

比如上图,我们从 b 点开始出发,经过 d,经过 c,最后回到 b 的时候发现,我到达我自己居然是一个负数!那么我们每更新一次,都会更小,这就叫做负权回路,面对这种情况,神仙难救,不用管好吧,但是我们还是可以判断一下的,在贝尔曼福特算法结束了之后,再更新一轮,如果发现他还能更新,就意味着里面有负权回路
如下:
// 还能更新就是带负权回路
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
// srci -> i + i ->j
if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
{
return false;
}
}
}Floyd-Warshall 弗洛伊德算法
这个算法就是动态规划
所以我们直接列举情况,我们要想知道从 i 点到 j 点的最短路径的话,我们就会经过 k 点,那么我们只需要比较一下,经过 k 点和不经过 k 点那个更短即可
但是我们需要注意的就是,i->k 和 k->j 两条边存在,如果根本没有这两条边的话,那就没必要比较了
以上就是弗洛伊德算法的全部了,如果你会了动态规划的话,那就很简单,动态规划没掌握的话,那就遭老罪了,所以建议学弗洛伊德算法之前,学一学动态规划
图示如下:

代码如下:
void FloydWarshall(vector<vector<W>>& vvDist)
{
size_t n = _vertexs.size();
vvDist.resize(n);
// 初始化权值和路径矩阵
for (size_t i = 0; i < n; ++i)
vvDist[i].resize(n, MAX_W);
// 直接相连的边更新一下
for (size_t i = 0; i < n; ++i)
for (size_t j = 0; j < n; ++j)
{
if (_matrix[i][j] != MAX_W)
vvDist[i][j] = _matrix[i][j];
if (i == j)
vvDist[i][j] = W();
}
// abcdef a {} f || b {} c
// 最短路径的更新i-> {其他顶点} ->j
for (size_t k = 0; k < n; ++k)
for (size_t i = 0; i < n; ++i)
for (size_t j = 0; j < n; ++j)
// k 作为的中间点尝试去更新i->j的路径
if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W
&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
{
vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
// 找跟j相连的上一个邻接顶点
// 如果k->j 直接相连,上一个点就k,vvpPath[k][j]存就是k
// 如果k->j 没有直接相连,k->...->x->j,vvpPath[k][j]存就是x
}
}结语
这篇文章到这里就结束啦!!~( ̄▽ ̄)~*
如果觉得对你有帮助的,可以多多关注一下喔