离散中偏序集、乘积群、关系的性质和集合的相关证明

离散证明题（三）
9.令❄是定义在有限集合A上的一个二元运算，若对于∀a,b∈A，❄满足①a=a❄a②a❄b=b❄a③a❄(b❄c)=(a❄b)❄c,在A上定义一个关系C比如a≤b<=>a=a❄b.
证明：(1)(A,≤)是一个偏序集 (2)∀a,b∈A,a∧b=a❄b
proof:
(1)①设a∈A，a=a❄a<=>a≤a，所以≤满足自反性reflexive
②设a,b∈A，如果a≤b且b≤a，
则有a≤b<=>a=a❄b，
又有b≤a<=>b=b❄a，
因为a❄b=b❄a
所以a=b,≤满足反对称性anti-symmetric
③设a,b,c∈A，
若a≤b，b≤c,则a=a❄b且b=b❄c,
那么就可以知道a=a❄(b❄c) =(a❄b)❄c = a❄c,
由a=a❄c<=>a≤c得出a≤c,所以≤满足传递性transitive
注：证明(A,≤)是一个偏序集就要证明≤在A上满足自反性reflexive，反对称性anti-symmetric，传递性transitive
(2) ①a❄b=a❄(b❄b)
=(a❄b)❄b
<=>a❄b≤b
②a❄b=b❄a
=b❄(a❄a)
=(a❄b)❄a
<=>a❄b≤a
到此可以说明a❄b是a和b的下边界
③假设c为a,b的一个下边界，那么c≤a且c≤b
c=(c❄a)❄b
=c❄(a❄b)
<=>c≤(a❄b)
由此可知a❄b为a,b的最大下边界
10.令(S,❄)和(T,❄’) 为两个群，证明(S×T,❄’’)也是一个群，其中❄’‘的运算定义为(s₁,t₁)❄’’(s₂,t₂)=(s₁❄s₂,t₁❄’t₂)
proof:
①假设(s₁,t₁),(s₂,t₂)∈S×T,因为(s₁,t₁)❄’’(s₂,t₂)=(s₁❄s₂,t₁❄’t₂)，所以❄’‘是一个二元运算binary operation
② (s₁,t₁)❄’’((s₂,t₂)❄’’(s₃,t₃))
=(s₁,t₁)❄’’(s₂❄s₃,t₂❄’t₃)
=(s₁❄(s₂❄s₃),t₁❄(t₂❄’t₃))
=((s₁❄s₂)❄s₃,(t₁❄t₂)❄’t₃)
=((s₁,t₁)❄’’(s₂,t₂))❄’’(s₃,t₃)
所以❄’‘满足结合律
③因为(S,❄)和(T,❄’) 为两个群，
所以∃e∈S，使得e❄s=s❄e=s （e是幺元）
∃e’∈T，使得e’❄’t=t❄’e‘=t （e’是幺元）
由(s₁,t₁)❄’’(s₂,t₂)=(s₁❄s₂,t₁❄’t₂)，可推得
(e,e’)❄’’(s,t)
=(e❄s,e’❄’t)
=(s,t)
(s,t)❄’’(e,e’)
=(s❄e,t❄’e’)
=(s,t)
所以∃(e,e’)∈S×T，使得(e,e’)❄’’(s,t)=(s,t)❄’’(e,e’)=(s,t)
也就是说(S×T,❄’’)是一个有幺元的半群
④因为(S,❄)和(T,❄’) 为两个群，
所以对∀s∈S，都有s❄s’=s’❄s=e（s’是逆元）
对∀t∈T，都有t❄t’=t’❄t=e’（t’是逆元）
由(s₁,t₁)❄’’(s₂,t₂)=(s₁❄s₂,t₁❄’t₂)，可推得
(s’,t’)❄’’(s,t)
=(s’❄s,t‘❄’t)
=(e,e’)
(s,t)❄’’(s’,t’)
=(s❄s’,t❄’t’)
=(e,e’)
所以对∀(s,t)∈S×T,都有(s’,t’)❄’’(s,t)=(s,t)❄’’(s’,t’)=(e,e’)
也即(s’,t’)是(S×T,❄’’)的逆元
综上可以说明(S×T,❄’’)是一个群
11.设R⊆A×A，对于任意的x,y,z∈A，如果(x,y)∈R且(y,z)∈R,那么(z,x)∈R，则称R为A上的循环关系。证明：若R是自反和循环的，则R具有对称性和传递性。
proof:
①设x,y∈A，因为R是自反的，所以(x,x)∈R，假设(x,y)∈R,因为R是循环的，由（x,x）∈R、(x,y)∈R可以得出（y,x）∈R,所以R具有对称性
②设x,y,z∈A，因为R是循环的，所以当(x,y)∈R且(y,z)∈R时，有(z,x)∈R，由①可知R是对称的，所以有(x,z)∈R, 由此可知R具有传递性.
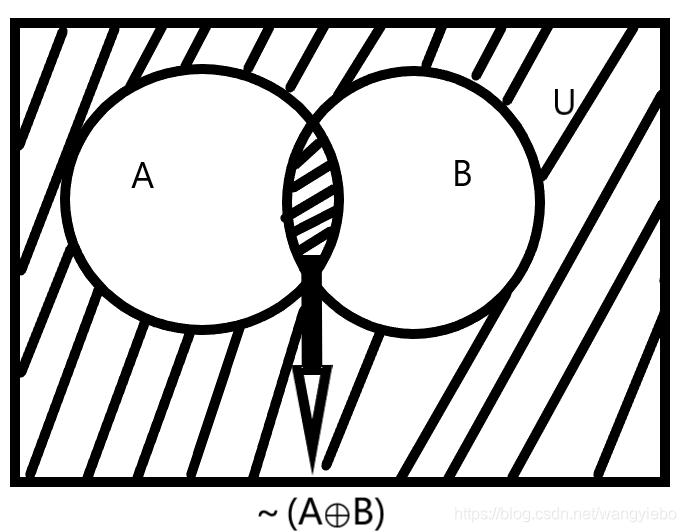
12.设A,B是集合，定义ⓧ环积运算如AⓧB=～(A⊕B)
证明:AⓧB=[A∪(～B)]∩[(～A)∪B]
proof：
由对称差的定义可知：(A⊕B)=(A-B)∪(B-A)
即{x|(x∈A and x∉B）or（x∈B and x∉A）}
那么AⓧB=～(A⊕B)即为{x|x∉A or x∈B）and（x∉B or x∈A）}
也就是x∈ (～A)∪B且x∈ (～B)∪A
即x∈[ (～A)∪B]∩ [(～B)∪A]
注：AⓧB图解如下所示