数学建模数据分析中的多元线性回归分析

多元线性回归分析
通过研究自变量 $X$ 和因变量 $Y$ 的相关关系，尝试去解释 $Y$ 的形成机制，进而达到通过 $X$ 去预测 $Y$ 的目的 。

(1) 回归分析的简介

1. 相关性

• 相关性 $\ne$ 因果性。
• 因果关系很难探究，因此通过探究相关性来代替。

2. 因变量 $Y$

• 因变量一般是要研究的核心变量。
• 因变量的分类:
  • 连续数值型变量：比如GDP的增长率。
  • 0-1型变量：比如将 $Y$ 设定为二值变量 $Y=1$ 表示女性，$Y=0$ 表示男性。
  • 定序变量：比如在层次分析法中对目标的打分(1：稍微好，3：更好等等)
  • 计数变量
  • 生存变量

3. 自变量 $X$

• 用 $X$ 来解释或者预测因变量 $Y$,因此 $X$ 也称为解释变量，$Y$ 称为被解释变量。

4. 回归分析的用途

• 分析哪些 $X$ 真的与因变量 $Y$ 相关。
• 分析真的与变量 $Y$ 相关的 $X$ 与 $Y$ 的关系是正还是负。
• 在真正相关的 $X$ 中计算出不同的回归系数，进而可以知道不同的 $X$ 的不同的重要性。

5. 数据的分类

• 横截面数据：在某一时间收集的不同对象的数据。如：2020年的全国各省GDP。
• 时间序列数据：对同一对象在不同时间的连续观测数据。如：陕西省1945-2020的GDP。
• 面板数据：横截面数据与时间序列数据综合起来的一种数据类型。如：1945-2020全国各省的GDP。

⭐️不同分类的数据的处理方案：

横截面数据	时间序列数据	面板数据
多元线性回归	移动平均、指数平滑、ARIMA、GARCH、VAR、协积	固定效应，随机效应，静态面板，动态面板

(2) 多元线性回归分析

1. 一元线性回归与拟合的对比

• 一元线性函数拟合：
  • 设样本点 $(x_i,y_i)(i=1,\dots ,n)$
  • 设置拟合曲线 $y=kx+b$
  • 设定拟合值为 $\widehat{y_i}=k{x}_i+b$
  • 目标：$\hat{k},\hat{b}=ar{g}_{k,b}(min(\sum _{i=1}^n(y-\hat{y}{)}^2)=ar{g}_{k,b}(min(\sum _{i=1}^n(\widehat{y_i}-k{x}_i-b{)}^2)$，即求 $\hat{k},\hat{b}$ 使 $\sum _{i=1}^n(y-\hat{y}{)}^2$ 最小。
• 一元线性回归：
  • 设 $x$ 是自变量， $y$ 是因变量，并且两者之间满足关系$$y={\beta }_0+{\beta }_1{x}_{+}\mu$$
  • 其中 ${\beta }_1,{\beta }_0$ 为回归系数，$\mu$ 是一个无法观测的扰动项，则预测值为$$\hat{y}={\beta }_0+{\beta }_1\hat{x}$$
  • 记 ${\hat{\mu }}_i=y_i-{\hat{\beta }}_0-{\hat{\beta }}_1{x}_i$ 为残差 。目标为 ${\hat{\beta }}_0,{\hat{\beta }}_1=ar{g}_{{\beta }_0,{\beta }_1}(min(\sum _{i=1}^n{\widehat{{\mu }_i}}^2))$,即求 $\widehat{{\beta }_0},\widehat{{\beta }_1}$ 使 $\sum _{i=1}^n(\widehat{{\mu }_i}{)}^2$ 最小。

⭐️ 从上面看来，一元线性拟合和一元线性回归在本质上是一样的，都是求出一条曲线，保证所有样本点到该曲线的距离和最短。

2. 对于线性的理解

• 不一定必须满足完全一样的形式 $y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k+\mu$。
• 只要可以将数据转化成类似的形式就可以按照线性的处理方式处理(导入数据之前提前计算好即可)：
  • $y={\beta }_0+{\beta }_{1}lnx+\mu$
  • $lny={\beta }_0+{\beta }_{1}x+\mu$
  • $y={\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2+\mu$
  • $y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_1{x}_2+\mu$

3. 对内生性的说明

• 假设模型为：$y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_l{x}_k+\mu$。
• 如果误差项 $\mu$ 与自变量 $x$ 均不相关则称该模型具有外生性，如果相关则存在内生性。
• 内生性会导致回归系数估计的不准确，不满足无偏性和一致性。

4. 对变量的说明

• 核心解释变量：最关心的变量，希望得到对其系数的一致性估计(随着样本数量的增大，系数收敛到某个值)。
• 控制变量：对于方程中的其他变量，把它们也放入回归方程，主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素，以避免遗漏变量偏差。
• 可以不要求控制变量外生（即允许控制变量与扰动项相关），而只要在给定控制变量的条件下，核心变量与扰动项不相关即可。

5. 对回归系数的解释

• 一般的多元线性回归： $\hat{y}={\hat{\beta }}_0+{\hat{\beta }}_1{x}_1+\cdots {\hat{\beta }}_k{x}_k$ ，一般不考虑常数 ${\hat{\beta }}_0$。对于其他的系数 ${\hat{\beta }}_i$ 表示在控制其他变量不变的前提下，$x_i$ 每增加一个单位对 $y$ 造成的变化。
  也可以理解成偏导数的形式：$${\hat{\beta }}_m=\frac{\partial y}{\partial x_i}$$
• 双对数模型：$lny=a+b$ $lnx+\mu$ 表示 $x$ 每增加 $1\%$ ，$y$ 相应变化 $b\%$。
• 半对数模型：$lny=a+bx+\mu$ 表示 $x$ 每增加一个单位 ，$y$ 相应变化 $(100b)\%$。
• 半对数模型：$y=a+b$ $lnx+\mu$ 表示 $x$ 每增加 $1\%$，$y$ 相应变化 $b/100$。

6. 对特殊变量的说明

6.1. 虚拟变量

• 用于处理自变量中的定性变量，比如性别，地域，年级等。

$①$ 单分类的虚拟变量：

• 例如研究性别对工资的影响：
  $y={\beta }_0+{\theta }_{0}Female+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k+\mu$
  $Female=0$ 代表该样本为男性，$Female=1$ 代表该样本为女性。
  核心解释变量为：$Female$。控制变量为：$x_m(m=1,2,\dots ,k)$。
• 解释：样本为女性：$E(y|Female=1,其它变量给定)={\theta }_0\times 1+C$, 样本为男性：$E(y|Female=0,其它变量给定)={\theta }_0\times 0+C$，因此 ${\theta }_0=E(y|Female=1,其它变量给定)-E(y|Female=0,其它变量给定)$,也就是在给定条件下，女性的平均工资与男性的平均工资的差异。

$②$ 多分类的虚拟变量：

• 例如研究地域区别对贷款成功率的影响：
  $$Succes{s}_i=\sum _k{\beta }_n\times Provinc{e}_i^{(k)}+\lambda \times Control{s}_i+\alpha +{\mu }_i$$
• 当第 $i$ 个样本的借款人来自 第 $k$ 个省份，则除去 $Provinc{e}_i^{(k)}=1$ 以外，其它的都取 $0$，如果第 $k$ 个省份是内蒙古，则所有的 $Provinc{e}_i$ 均取 $0$。(将内蒙古作为对照组)
• 为避免多重共线性的影响，引入的虚拟变量的个数一般是分类数减 $1$。

6.2. 含有交互项的变量

• 例如：$price$：房价，$sqrft$：住房面积，$bdrms$：卧室数量，$bthrms$：卫生间数量。
  $$price={\beta }_0+{\beta }_{1}sqrt+{\beta }_{2}bdrms+{\beta }_{3}sqrft\times bdrms+{\beta }_{4}bthrms+\mu$$
• 可以看到这里含有交叉项$$\frac{\partial price}{\partial sqrft}={\beta }_2+{\beta }_{3}bdrms$$
• 若 ${\beta }_3>0$ 则意味着，住房面积越大，增加一间卧室导致价格上升的越快。

7. 拟合优度 $R^2$ 较低的解决方法

• 回归分为解释性回归和预测型回归。对解释性回归不用太在意 $R^2$ 的大小。
• 对模型进行调整，例如对数据取对数或者进行平方。

8. 扰动项与异方差

• 一般情况下是球形扰动项(满足“同方差”和“无自相关”两个条件)。
• 横截面数据容易出现异方差问题，时间序列数据容易出现自相关问题。
• 解决方案：使用 OLS+稳健的标准误。

9. 多重共线性

• 症状：
  • 虽然整个回归方程的 $R^2$ 较大、$F$ 检验也很显著，但是单个的 $t$ 检验却不显著，或者系数估计值不合理，甚至符号与理论预期相反。
  • 增减解释变量使系数的估计值发生较大变化。
• 检验：
  • 方差膨胀因子：$VIF$。
  • 假设现在有 $k$ 个变量，那么第 $m$ 个自变量的 $VI{F}_m=\frac{1}{1-R_{1-k\backslash m}^2}$ ,其中 $R_{1-k\backslash m}^2$ 代表将第 $m$ 个自变量作为因变量，对剩下的 $k-1$ 个自变量进行回归得到的拟合优度，明显 $VI{F}_m$ 越大，$R_{1-k\backslash m}^2$ 越大，代表第 $m$ 个变量与其他变量的相关性越大。
  • 定义回归模型的 V I F = m a x { V I F 1 , V I F 2 , … , V I F k } VIF=max\{VIF_1,VIF_2,\dots,VIF_k\} VIF=max{ VIF1​,VIF2​,…,VIFk​}。
  • 当 $VIF>10$ 就说该回归方程存在严重的多重共线性。
• 解决：
  • 不关心具体的回归系数，只关心预测与解释能力，在整个方程显著的前提下，不用担心多重共线性。
  • 关心具体的回归系数，但并不影响其显著性的时候，不用在意。有多重共线性都显著，没有多重共线性只能更显著。
  • 如果影响到：增大样本容量，剔除导致严重共线性的变量，对模型进行修改。

(3) stata的使用

• 文件导入：注意要勾选，将第一行作为变量名。

• 写代码，类似matlab的脚本。

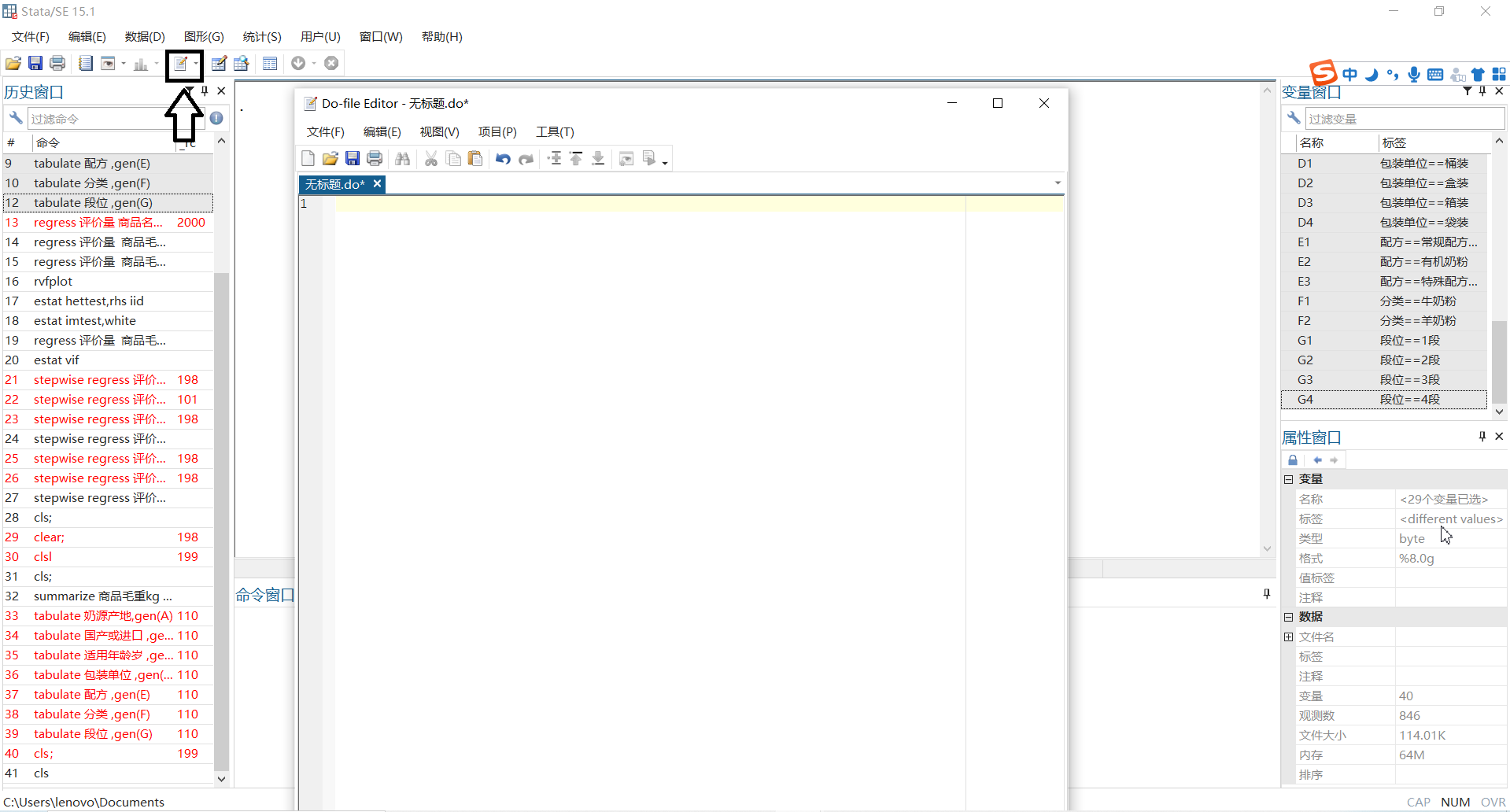
• 定量数据：summarize 变量1 变量2 变量3...

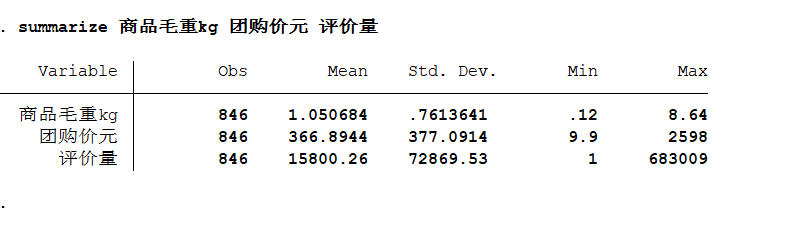
• 定性数据：tabulate 变量,gen(A)生成对应的虚拟变量(以A开头)。

• 普通回归：regress y x1 x2 ... xk（默认使用OLS，普通最小二乘估计）。

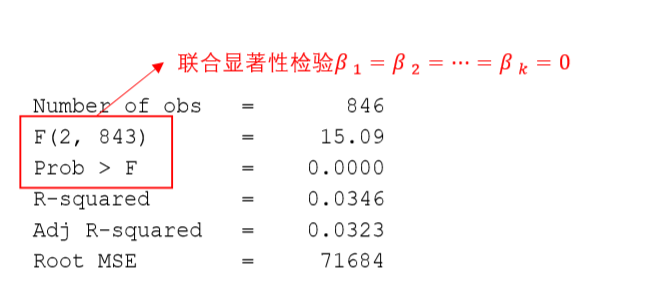
只有在 $p$ 值足够小，也就是否定原假设之后这个回归才能使用。原假设也就是 ${\beta }_1={\beta }_2=\cdots ={\beta }_k$。

只有在 $p$ 值足够小，也就是否定原假设之后这个回归系数才有意义。原假设就是 ${\beta }_i=0$。

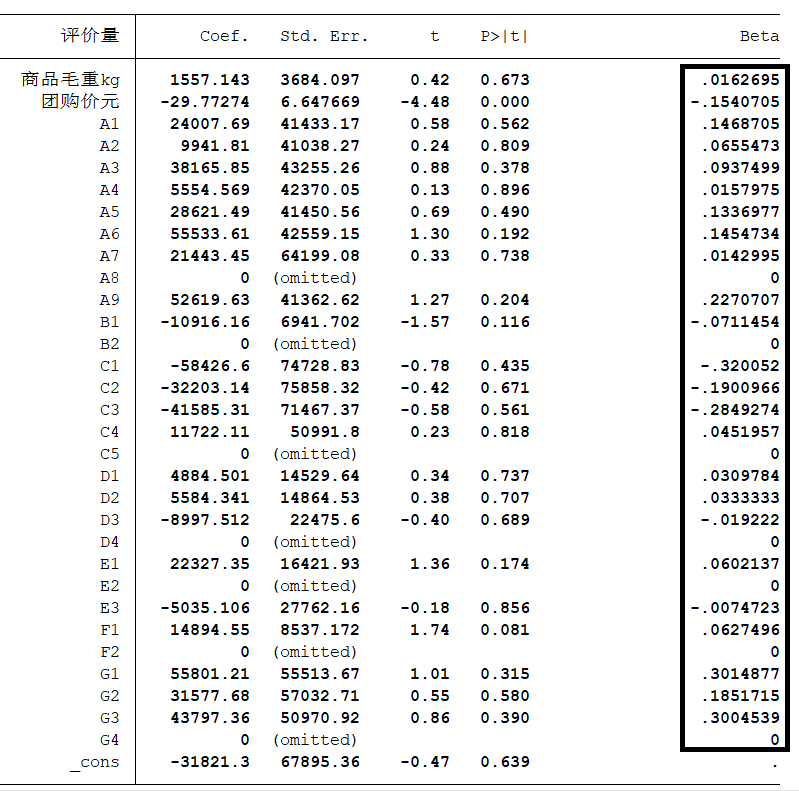
• 标准化回归：regress y x1 x2 ... xk,beta，也就是对数据进行标准化，将原数据减去它的均数后再除以该变量的标准差。在系数显著的前提下，绝对值越大说明对因变量的影响越大。

  

• 逐步回归：

  • stepwise regress y x1 x2 ... xk,pe(#1) 向前逐步回归，显著才加入到模型中。#1填入显著性水平的值，如0.05等。
  • stepwise regress y x1 x2 ... xk,pr(#2) 向前逐步回归，不显著就剔除出模型。#2填入显著性水平的值，如0.05等。
  • 注意此时 $x_1,x_2,\cdots ,x_k$ 之间不能存在完全共线性，也就是对每一组虚拟变量要剔除出一组作为对照组。
  • 可以在后面在加beta或robust。注意要直接加，不要再填逗号，如stepwise regress y x1 x2 ... xk,pr(#2)robust。

• 使用OLS与稳健的标准误：regress y x1 x2 ... xk,robust。可以看出，此时的显著不为 $0$ 的变量明显增多。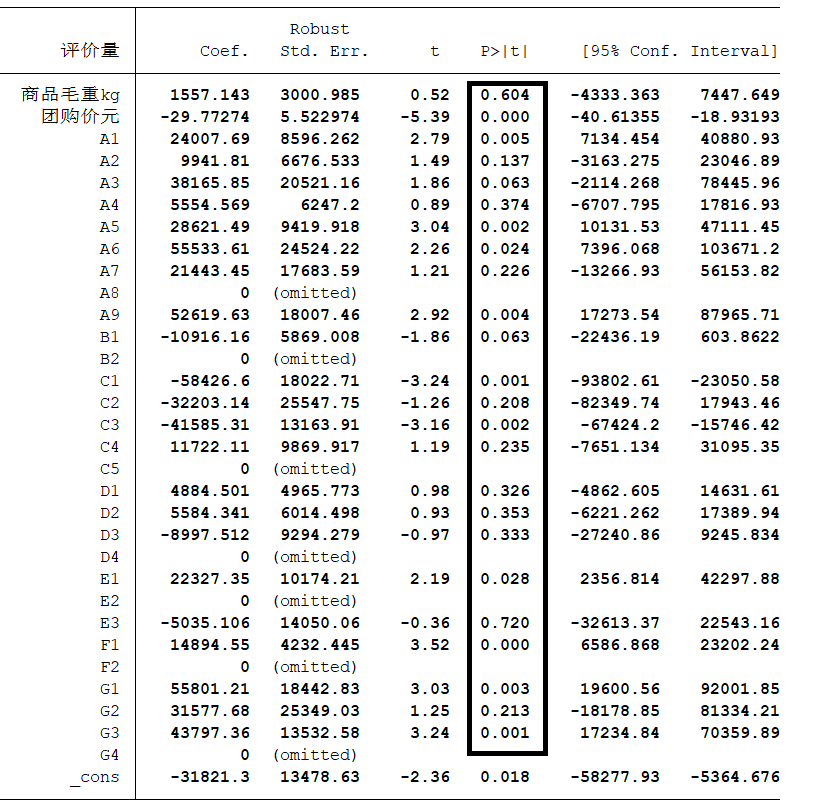

  

• 异方差的检验：estat imtest,white (回归结束后使用)，注意原假设为：不存在异方差

• 多重共线性的检验：estat vif (回归结束后使用)，$VIF>10$ 就认为存在严重的多重共线性。