数学建模与数据分析中的因子分析

因子分析
在某种程度上可以看成是主成分分析法的推广，优势主要体现在解释选取的综合因子时更加容易

(1) 因子分析实例

为了评价高中学生将来进入大学时的学习能力，抽了 $200$ 名高中生进行问卷调查，共 $50$ 个问题。所有这些问题可简单的归结为阅读理解、数学水平和艺术修养这三个方面。这就是一个因子分析模型，每一个方面就是一个因子。

(2) 因子分析前的检验

• KMO检验
  • KMO 值越接近 $1$，意味着变量间的相关性越强，KMO 值越接近 $0$，意味着变量间的相关性越弱。相关性越强越适合进行因子分析。
  • KMO> $0.9$ 非常适合进行因子分析，$0.9$ >KMO> $0.8$ 适合进行因子分析，$0.8$ >KMO> $0.7$ 一般，$0.7$ 不太适合。
• 巴特利特球性检验
  • 原假设为：相关系数矩阵是一个单位矩阵 (不适合做因子分析，指标之间的相关性太差，不适合降维)。
  • 备择假设为：适合做因子分析。
  • 使用 SPSS 可以计算出 $p$ 值。

(3) 因子分析原理

• 大小为 $n\times p$ 的随机向量 $x=(x_1,x_2,\dots ,x_p{)}^T$，均值为 $\mu =({\mu }_1,{\mu }_2,\dots ,{\mu }_p{)}^T$，特殊因子向量 $ϵ=({ϵ}_1,{ϵ}_2,\dots ,{ϵ}_p{)}^T$，公因子向量 $f=(f_1,f_2,\dots ,f_p{)}^T$，载荷矩阵 $A_{p\times m}=(a_{ij}{)}_{p\times m}$ ，注意这里 $x_i，{\mu }_i，{ϵ}_i，f_i$ 都是 $n\times 1$ 维的向量。
• 因子分析的一般模型
  $$\{\begin{array}{rl}{x}_1& ={\mu }_1+a_{11}{f}_1+a_{12}{f}_2+\cdots +a_{1m}{f}_m+{ϵ}_1\\ x_2& ={\mu }_2+a_{21}{f}_1+a_{22}{f}_2+\cdots +a_{2m}{f}_m+{ϵ}_2\\ & ⋮\\ x_p& ={\mu }_p+a_{p1}{f}_1+a_{p2}{f}_2+\cdots +a_{pm}{f}_m+{ϵ}_p\end{array}$$
  表示为矩阵的形式：$$x=\mu +Af+ϵ$$
• 对模型的相关假设
  $$\{\begin{array}{rl}& E(f)=0\\ & E(ϵ)=0\\ & Var(f)=I\\ & Var(ϵ)=D=diag({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_p^2)\\ & Cov(f,ϵ)=0\end{array}$$
  公因子不相关并且具有单位方差，特殊因子和公因子也不相关。
• 解释：特殊因子向量其实就像噪声，是一个无关紧要的向量，公因子向量表现的就是提取的各个公因子。

(4) 因子模型的性质

$①$ $x$ 的协方差矩阵的分解
$$\begin{array}{rl}Var(x)& =E[(x-\mu )(x-\mu {)}^T]=E[(Af+ϵ)(Af+ϵ{)}^T]\\ & =AE(f{f}^T)A^T+AE(f{ϵ}^T)+E(ϵf^T)A^T+E(ϵ{ϵ}^T)\\ & =AVar(f)A^T+Var(ϵ)\\ & =A{A}^T+D=\sum \end{array}$$
$②$ ⭐️因子载荷不唯一 （由于载荷的不唯一才可以通过调整载荷矩阵使解释变得更容易）

• 取 $T$ 为任意一个 $m\times m$ 的正交矩阵，并取 $A^{\ast }=AT$，$f^{\ast }=T^{T}f$，将 $A^{\ast }$ 与 $f^{\ast }$ 代入相关假设之中，发现还成立，因此可以将 $A$ 改为 $A^{\ast }$。

(5) 因子载荷矩阵的统计意义

• 原始变量 $x_i$ 与公因子 $f_j$ 之间的协方差
  $$Cov(x_i,f_j)=\sum _{k=1}^m{a}_{ik}Cov(f_k,f_j)+Cov({ϵ}_i,f_j)=a_{ij}$$
  若 $x$ 已经经过标准化，则 $a_{ij}=\rho (x_i,f_j)$ 表示 $x_i$ 和 $f_j$ 之间的相关系数。
• $A$ 的行元素平方和 $h_i^2=\sum _{j=1}^m{a}_{ij}^2$ ———原始变量 $x_i$ 对公因子依赖的程度。
  • 当 $x$ 没有进行标准化时
    $$\begin{array}{rl}{\sigma }_{ii}=V(x_i)& =a_{i1}^{2}V(f_1)+a_{i2}^{2}V(f_2)+\cdots +a_{im}^{2}V(f_m)+V({ϵ}_i)\\ & =a_{i1}^2+a_{i2}^2+\cdots +a_{im}^2+{\sigma }_i^2\\ & =h_i^2+{\sigma }_i^2\end{array}$$
    其中 ${\sigma }_{ii}$ 称为个性方差。
  • 当 $x$ 进行过标准化之后
    $1=h_i^2+{\sigma }_i^2$
• $A$ 的列元素平方和 $g_j^2=\sum _{i=1}^p{a}_{ij}^2$ ———公因子 $f_j$ 对 $x$ 的贡献。
  • 取 $g_j^2=\sum _{i=1}^p{a}_{ij}^2(j=1,2,\dots ,m)$
    $$\begin{array}{rl}\sum _{i=1}^{p}V(x_i)& =\sum _{i=1}^p{a}_{i1}^{2}V(f_1)+\sum _{i=1}^p{a}_{i2}^{2}V(f_2)+\cdots +\sum _{i=1}^p{a}_{im}^{2}V(f_m)+\sum _{i=1}^{p}V({ϵ}_i)\\ & =g_1^2+g_2^2+\cdots +g_m^2+\sum _{i=1}^p{\sigma }_i^2\end{array}$$
  • $g_j^2$ 是衡量公因子 $f_j$ 重要性的一个尺度，可视为公因子 $f_j$ 对 $x$ 的贡献。

(6) 参数估计

• $x_1,x_2,\dots ,x_n$ 是一组 $p$ 维的样本。则可以估计 $\mu$ 和 $\sum$ 分别为 $$\overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$$
  $$S^2=\frac{1}{n-1}\sum _{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T$$
• 还需要估计因子载荷矩阵 $A$ 与个性方差矩阵 $D=diag({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_p^2)$
  • 主成分法
  • 最大似然法
  • 主因子法

(7) 确定公共因子的个数

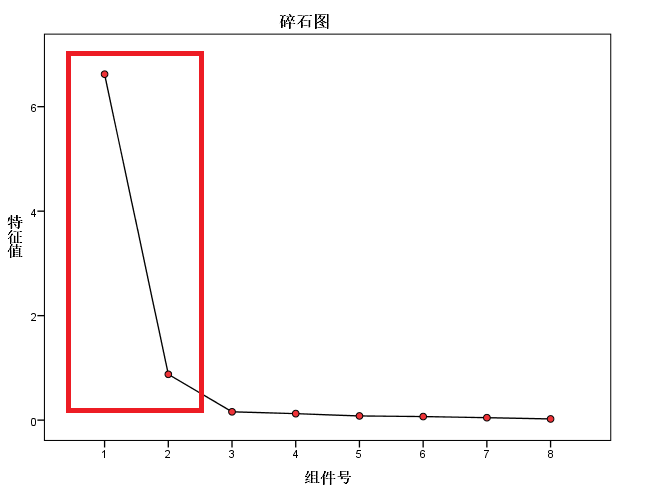
碎石检验：当某个特征值较前一特征值出现较大的下降，而这个特征值较小，其后面的特征值变化不大，说明添加相应于该特征值的因素只能增加很少的信息，因此只取前几几个特征值。

(8) 因子旋转

• 因子旋转的目的，使公共因子的载荷系数的绝对值更可能接近 $0$ 或 $1$，这样可以使因子更好分析。
• 使用 SPSS。

(9) 因子得分

• 反过来将公共因子表示为原变量的线性组合。
  $$\{\begin{array}{rl}{f}_1& =b_{11}{x}_1+b_{12}{x}_2+\cdots +b_{1m}{x}_p\\ f_2& =b_{21}{x}_1+b_{22}{x}_2+\cdots +b_{2m}{x}_p\\ & ⋮\\ f_m& =b_{m1}{x}_1+b_{m2}{x}_2+\cdots +b_{mp}{x}_p\end{array}$$
  $b_{ij}$ 就是第 $i$ 个因子的得分对应于第 $j$ 个变量。
• 常用 Anderson-Rubin 方法和 Bartlett 得分。