数学建模与数据分析中的时间序列分析

时间序列分析
将某种现象的指标数值按照时间顺序排列而成的数值序列。

(1) 时间序列的基本概念

1. 组成要素

• 时间要素。
• 数值要素。

2. 时间序列的分类

• 时期序列：数值要素反映现象在一定时期内的表现。(历年的 GDP )
• 时点序列：数值要素反映现象在一定时间点上的瞬时水平。(每次模拟考试的成绩)
• 时期序列可加（相加表示更长一段时期的数值），时点序列不可加。(类比速度和加速度)

3. 时间序列的分解

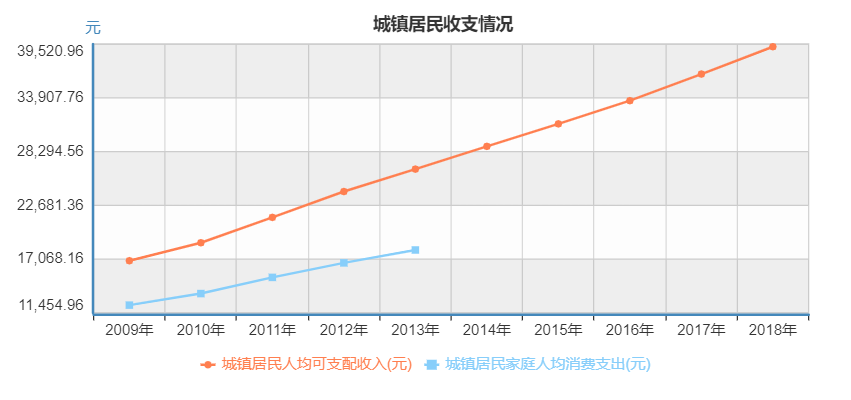
① 长期变动趋势 T

• 表示统计指标在较长一段时间，受到某些长期因素(政策，生产力等)的影响，表现持续上升或持续下降的趋势。

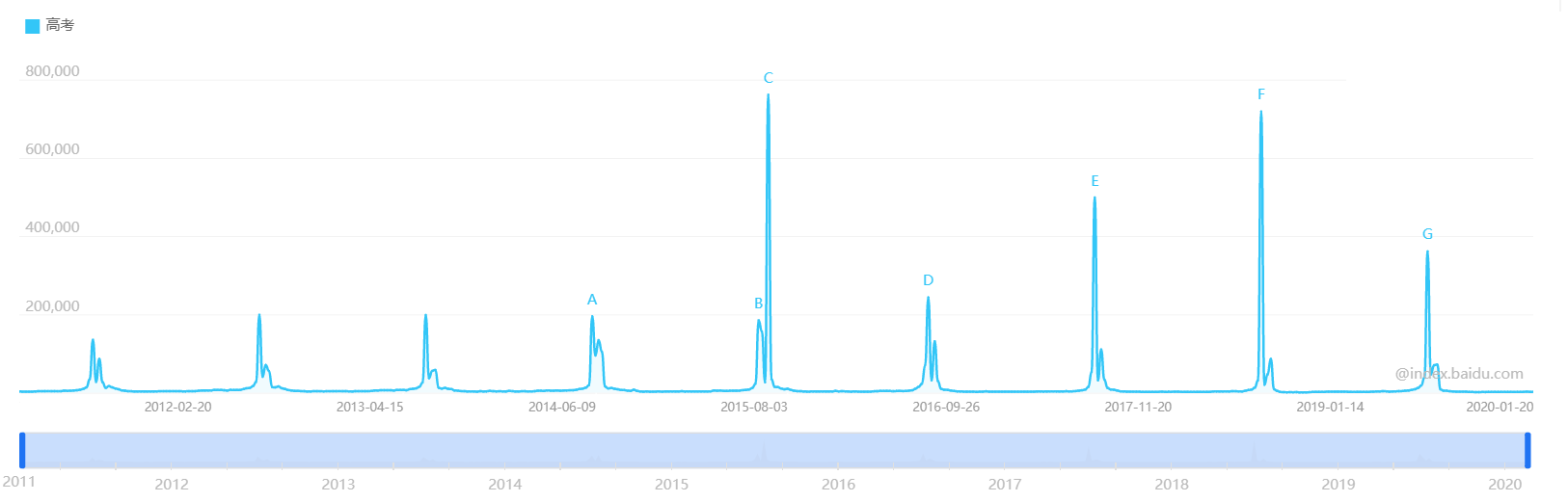
② 季节趋势 S

• 由于季节的转变使指标数据发生周期性的变动。季节是广义的，可以为月、季、周，但不能是年。关键的核心在于周期性。

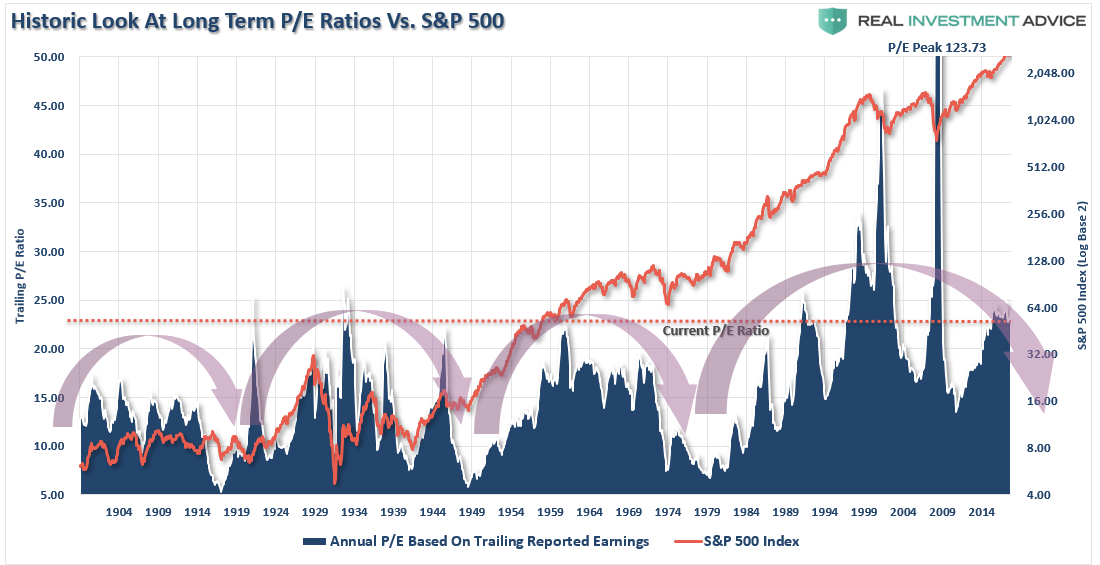
③ 循环趋势 C

• 与季节趋势的不同在于一方面时间通常以年作为单位，另一方面表现的只是增减趋势的交替出现，而不一定有严格的周期性。

④ 不顾则变动 I

• 扰动项，没有规律也不可预测，是偶然因素导致的。

4. 时间序列的分解模型

• 叠加模型：适用于四种变动之间是相互独立的关系。$$Y=T+S+L$$
• 乘积模型：适用于四种变动之间存在相互影响的关系。$$Y=T\times S\times L$$
  $Y$ 表示指标数值的最终变动。
• 选取准则：
  • 数据必须具有周期性。月份，季度数据可以用，但年份数据不能用。
  • 不存在季节波动，两者都可以选择。
  • 存在季节波动，随时间推移，季节波动变动较大可以优先考虑乘积模型，季节波动变化不大可以优先考虑叠加模型。

(2) 季节分解

• 使用 SPSS 软件，选取叠加模型还是乘积模型。

(3) 指数平滑法

1. 简单指数平滑法

• 适用于不含趋势和季节成分的情况。
• 类似于 ARIMA(0,1,1)。
• 令 $x_t$ 为 $t$ 时刻的观测数据， $S_t$ 为第 $t$ 期的平滑值，再令 $S_t={\hat{x}}_{t+1}$ 为第 $t+1$ 期的预测值。满足如下条件：$${\hat{x}}_{t+1}=\alpha x_t+(1-\alpha ){\hat{x}}_t$$
  其中 $0\le \alpha \le 1$ 称为平滑系数。
• 代入展开式为：$${\hat{x}}_{t+1}=\alpha x_t+\alpha (1-\alpha )x_{t-1}+\alpha (1-\alpha {)}^2{x}_{t-2}+\cdots$$
• 注意：由公式形式决定，简单指数平滑只能预测一期。

2. 线性趋势模型

• 适用于线性趋势，不含季节成分。
• 类似于 ARIMA(0,2,2)。
• $l_t$ 表示在 $t$ 时期的水平估计值，$b_t$ 表示在 $t$ 时刻的趋势估计值(斜率)，$0\le \alpha \le 1$ 为水平的平滑系数，$0\le \beta \le 1$ 为趋势的平滑系数。
  $$\{\begin{array}{rlr}{l}_t=\alpha x_t+(1-\alpha )(l_{t-1}+b_{t-1})& & (水平平滑方程)\\ b_t=\beta (l_t-l_{t-1})+(1-\beta )b_{t-1}& & (趋势平滑方程)\\ {\hat{x}}_{t+h}=l_t+h{b}_t,h=1,2,3,\cdots & & (预测方程)\end{array}$$
  影响 $b_t$ 的因素是水平的增量和上一期的 $b_{t-1}$ 的值，影响 $l_t$ 的是当前观测值 $x_t$，上一期的水平估计值 $l_{t-1}$ 和上一期的趋势估计值 $b_{t-1}$。预测方程可以用积分做类似的理解。

3. 阻尼趋势模型

• 适用线性趋势逐渐减弱且不含季节性因素。
• 类似于 ARIMA(1,1,2)。
• $l_t$ 表示在 $t$ 时期的水平估计值，$b_t$ 表示在 $t$ 时刻的趋势估计值(斜率)，$0\le \alpha \le 1$ 为水平的平滑系数，$0\le \beta \le 1$ 为趋势的平滑系数，$0<\varphi \le 1$ 为阻尼参数。
  $$\{\begin{array}{rlr}{l}_t=\alpha x_t+(1-\alpha )(l_{t-1}+\varphi b_{t-1})& & (水平平滑方程)\\ b_t=\beta (l_t-l_{t-1})+(1-\beta )\varphi b_{t-1}& & (趋势平滑方程)\\ {\hat{x}}_{t+h}=l_t+(\varphi +{\varphi }^2+\cdots +{\varphi }^h)b_t& & (预测方程)\end{array}$$
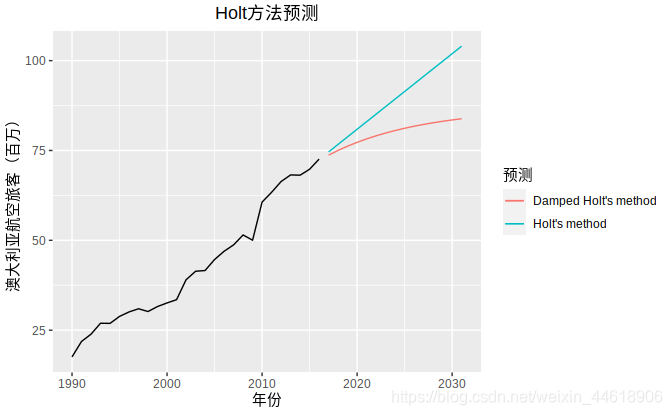
  可以看出当阻尼参数越接近 0 时，对原趋势的阻碍作用越大。

下面是一张阻尼与线性的预测图。

4. 简单季节趋势模型

• 适用有稳定的季节成分、不含趋势。
• 类似于 SARIMA(0,1,1) $\times$ (0,1,1)。
• $l_t$ 表示在 $t$ 时期的水平估计值，$s_t$ 表示在 $t$ 时刻的季节估计值，$0\le \alpha \le 1$ 为水平的平滑系数，$0\le \gamma \le 1$ 为趋势的平滑系数，$m$ 代表周期的长度，月为周期就是 12，季度为周期就是 4。
  $$\{\begin{array}{rlrl}{l}_t& =\alpha (x_t-s_{t-m})+(1-\alpha )l_{t-1}& & (水平平滑方程)\\ s_t& =\gamma (x_t-l_{t-1})+(1-\gamma )s_{t-m}& & (季节平滑方程)\\ {\hat{x}}_{t+h}& =l_t+s_{t+h-m(k+1)}，k=\lfloor \frac{h-1}{m}\rfloor & & (预测方程)\end{array}$$

5. Holt-Winters 加法模型

• 适用有稳定的季节成分、含线性趋势。
• 类似于 SARIMA(0,1,0) $\times$ (0,1,1)。
• $l_t$ 表示在 $t$ 时期的水平估计值，$s_t$ 表示在 $t$ 时刻的季节估计值，$0\le \alpha \le 1$ 为水平的平滑系数，$0\le \gamma \le 1$ 为趋势的平滑系数，$m$ 代表周期的长度，月为周期就是 12，季度为周期就是 4。
  $$\{\begin{array}{rlrl}{l}_t& =\alpha (x_t-s_{t-m})+(1-\alpha )(l_{t-1}+b_{t-1})& & (水平平滑方程)\\ b_t& =\beta (l_t-l_{t-1})+(1-\beta )b_{t-1}& & (趋势平滑方程)\\ s_t& =\gamma (x_t-l_{t-1}-b_{t-1})+(1-\gamma )s_{t-m}& & (季节平滑方程)\\ {\hat{x}}_{t+h}& =l_t+h{b}_t+s_{t+h-m(k+1)}，k=\lfloor \frac{h-1}{m}\rfloor & & (预测方程)\end{array}$$
• 水平方程表示在 $t$ 时刻，季节性调整的观察值与非季节性预测值之间的加权平均值。
• 季节性方程表示当前季节性指数和去年同一季节（即 $m$ 个时间段前）的季节性指数之间的加权平均值。

5. Holt-Winters 乘法模型

• 适用不稳定的季节成分、含线性趋势。
• 不存在 ARIMA 模型。
  $$\{\begin{array}{rlrl}{l}_t& =\alpha \frac{x_t}{s_{t-m}}+(1-\alpha )(l_{t-1}+b_{t-1})& & (水平平滑方程)\\ b_t& =\beta (l_t-l_{t-1})+(1-\beta )b_{t-1}& & (趋势平滑方程)\\ s_t& =\gamma \frac{x_t}{l_{t-1}+b_{t-1}}+(1-\gamma )s_{t-m}& & (季节平滑方程)\\ {\hat{x}}_{t+h}& =(l_t+h{b}_t)s_{t+h-m(k+1)}，k=\lfloor \frac{h-1}{m}\rfloor & & (预测方程)\end{array}$$
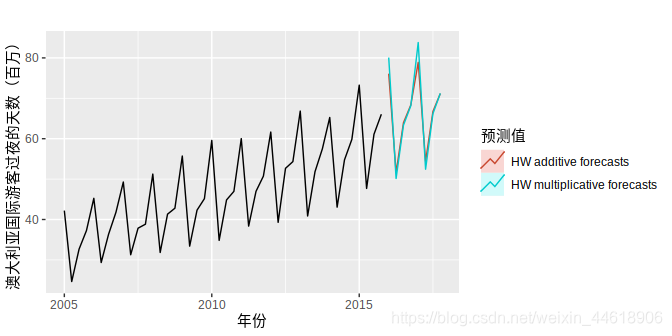
  下图为分别使用乘法模型与加法模型进行的预测：
  

(4) ARIMA 模型

1. 平稳时间序列和白噪声序列

• 协方差平稳(弱平稳)：时间序列 $x_t$ 满足以下三个条件
  • $E(x_t)=E(x_{t-s})=\mu$ 均值固定为常数。
  • $Var(x_t)=var(x_{t-s})={\sigma }^2$ 方差存在且为常数。
  • $Cov(x_t,x_{t-s})={\gamma }_s$ 协方差只与间隔 $s$ 有关，与 $t$ 无关。
• 白噪声：时间序列 $x_t$ 满足以下三个条件
  • $E(x_t)=E(x_{t-s})=0$
  • $Var(x_t)=Var(x_{t-s})={\sigma }^2$ 方差存在且为常数。
  • $Cov(x_t,x_{t-s})=0$

2. 差分方程与滞后算子

① 差分

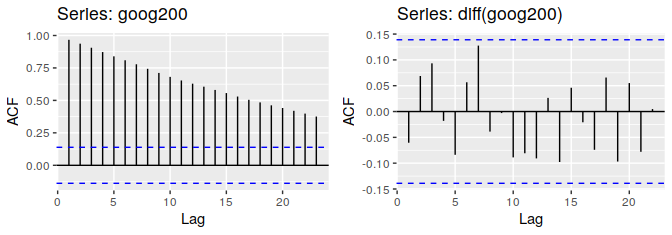
• 目的：通过作差来消除整体趋式或者季节变动的影响，比如下面 google 的股价，右边是做完差分后的状态。

② 差分方程

• 将某个时间序列变量表示为该变量的滞后项、时间和其他变量的一个函数方程。
• 自回归 $AR(p)$ 模型$$y_t={\alpha }_0+{\alpha }_1{y}_{t-1}+\cdots +{\alpha }_p{y}_{t-p}+{ϵ}_t$$
• 移动平均 $MA(q)$ 模型$$y_t={ϵ}_t+{\beta }_1{ϵ}_{t-1}+\cdots +{\beta }_q{ϵ}_{t-q}$$
• 自回归移动平均 $ARMA(p,q)$ 模型$$y_t={\alpha }_0+\sum _{i=1}^p{\alpha }_i{y}_{t-i}+{ϵ}_t+\sum _{i=1}^q{\beta }_i{ϵ}_{t-i}$$

③ 差分方程的特征方程

• 差分方程的齐次部分：只包含该变量自身及其滞后项。
• 特征方程：令齐次部分中的 $y_t=x^t$。
  例如，对自回归移动平均 $ARMA(p,q)$模型：
  齐次部分：$$y_t=\sum _{i=1}^p{\alpha }_i{y}_{t-i}$$
  特征方程(代入化简)：$$x^p={\alpha }_1{x}^{p-1}+{\alpha }_2{x}^{p-2}+\cdots +{\alpha }_p$$

④ 滞后算子

• 用来简化差分方程的书写。
• 用符号 $L$ 来表示滞后算子，$L^i{y}_t=y_{t-i}$
  • $LC=C$($C$为常数)
  • $(L^i+L^j)y_t=y_{t-i}+y_{t-j}$
  • $L^i{L}^j{y}_t=y_{t-i-j}$
• 差分的转化：
  • 一阶差分：$\Delta y_t=y_t-y_{t-1}=(1-L)y_t$
     
  • 二阶差分：$\Delta y_t=(y_t-y_{t-1})-(y_{t-1}-y_{t-2})=(1-L{)}^2{y}_t$
     
  • k 阶差分：$\Delta y_t=(1-L{)}^k{y}_t$

3. AR（p） 与 MA（q）

① AR（p）–p 阶自回归模型

$$y_t={\alpha }_0+{\alpha }_1{y}_{t-1}+\cdots +{\alpha }_p{y}_{t-p}+{ϵ}_t\rightleftharpoons (1-\sum _{i=1}^p{L}^i{\alpha }_i)y_t={ϵ}_t+{\alpha }_0$$

• ${ϵ}_t$ 是方差为 ${\sigma }^2$的白噪声序列。
• 自回归只能适用于预测与自身前期相关的现象。
• 自回归模型只能应用于平稳的序列，如果不平稳要先转换。
• 平稳的判断：
  转换成特征方程并解出 $p$ 个特征根 $x^p={\alpha }_1{x}^{p-1}+{\alpha }_2{x}^{p-2}+\cdots +{\alpha }_p$
  • $p$ 个特征根的模值均比 $1$ 小，平稳。
  • $p$ 个特征根中有 $k$ 个根模值恰好为 $1$，进行 $k$ 阶单位根过程，就是进行 $k$ 次差分。
  • $p$ 个特征根中存在一个根的模值比 $1$ 大，不平稳。
    

② MA(q)–q 阶移动平均模型

$$y_t={ϵ}_t+{\beta }_1{ϵ}_{t-1}+\cdots +{\beta }_q{ϵ}_{t-q}\rightleftharpoons y_t={ϵ}_t+(1+\sum _{i=1}^q{L}^i{\beta }_i){ϵ}_t$$

• 可以与AR模型之间相互转化。
• 平稳的判断：只要 $q$ 不取 $\infty$ 就平稳。
  

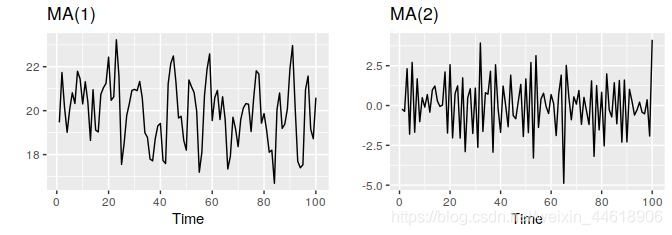
③ ARMA(p,q)–自回归移动平均模型

$$y_t={\alpha }_0+\sum _{i=1}^p{\alpha }_i{y}_{t-i}+{ϵ}_t+\sum _{i=1}^q{\beta }_i{ϵ}_{t-i}\rightleftharpoons (1-\sum _{i=1}^p{L}^i{\alpha }_i)y_t={\alpha }_0+(1+\sum _{i=1}^q{L}^i{\beta }_i){ϵ}_t$$

• 平稳性的判断：只与 AR§部分有关。

4. ACF与PACF

两个相关系数存在的条件都是时间序列是平稳的。

① ACF自相关系数

• 定义
  $${\rho }_s=\frac{cov(x_t,x_{t-s})}{\sqrt{Var(x_t)}\sqrt{Var(x_{t-s})}}=\frac{{\gamma }_s}{{\gamma }_0}$$ 由平稳时间序列的定义转化到 $\gamma$ 的比值，表明在一个平稳的时间序列中相隔 $s$ 期的两个时间点之间的相关系数。
• 样本的自相关系数$$r_s={\hat{\rho }}_s=\frac{{\sum }_{t=s+1}^T(x_t-\overline{x})(x_{t-s}-\overline{x})}{{\sum }_{t=1}^T(x_t-\overline{x}{)}^2}$$
• 如果时间序列是白噪声序列
  $${\rho }_s=\{\begin{array}{rlr}1& & s=0\\ 0& & s\ne 0\end{array}$$

② PACF偏自相关系数

• 它衡量的是在移除滞后量 $1,2,\cdots ,k-1$ 的影响的情况下, $y_t$ 和 $y_{t-k}$ 的关系，而之前 ACF在求$y_t$ 和 $y_{t-k}$ 的关系时并未去除中间变量的影响。

③ 使用PACF与ACF判断模型

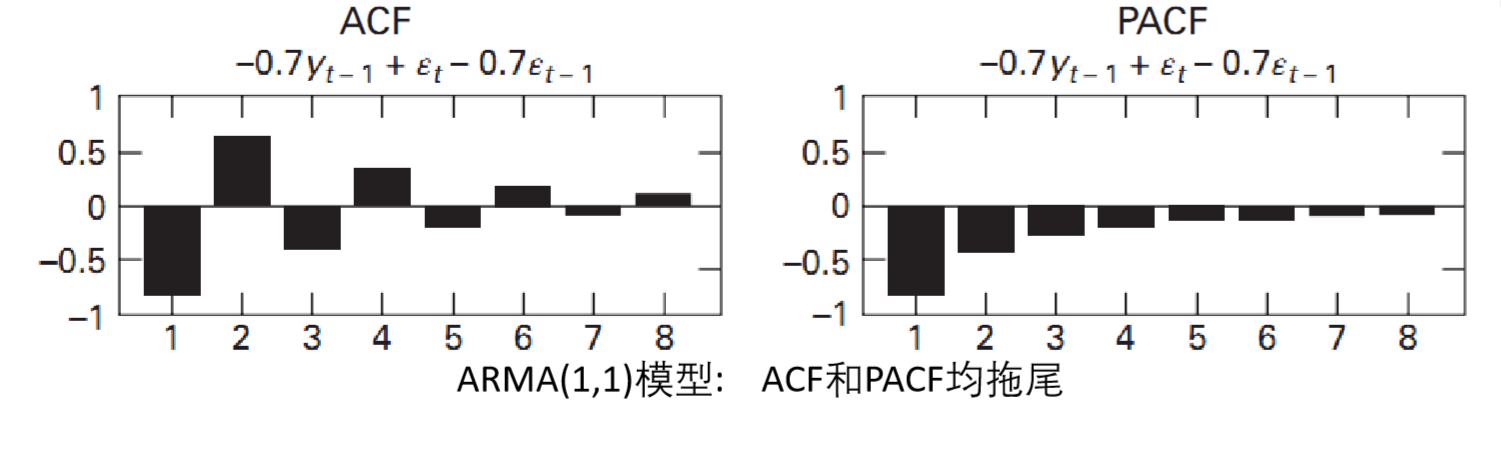
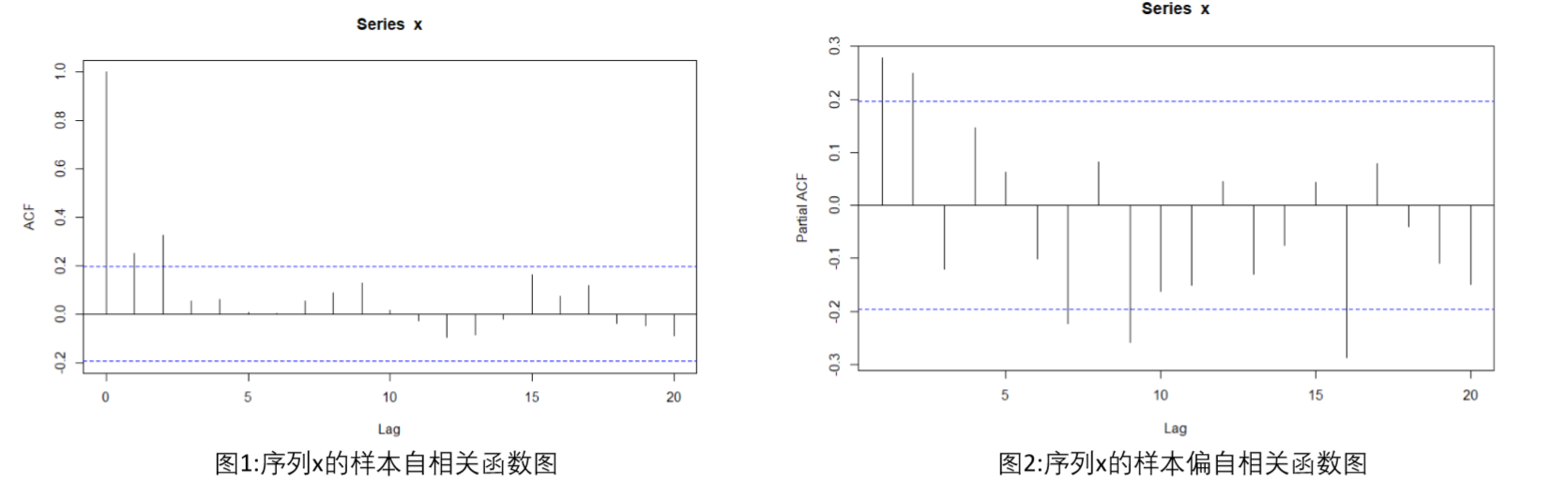
具体到数据图中：

• 自相关函数图拖尾，偏自相关函数图 $3$ 阶截止，因此为 AR(3)。

• 偏自相关函数图拖尾，自相关函数图 $2$ 阶截止，因此为 MA(2)。

5. 模型选择准则

• 赤池信息准则 AIC
  $$AIC=2(模型中参数的个数)-2ln(模型的极大似然函数值)$$
• 贝叶斯信息准则 BIC
  $$BIC=ln(T)(模型中参数的个数)-2ln(模型的极大似然函数值)$$
  $T$：样本个数。
  模型中参数个数：反映模型的复杂程度。
  模型的极大似然函数值：反映模型对于数据的拟合程度。

6. 判断模型是否识别完全

• 对残差进行检验，如果是白噪声说明识别完全，否则表示识别不完全。
• Q 检验
  • $H_0:{\rho }_1={\rho }_2=\cdots ={\rho }_s=0,H_1:$ 至少有一个 ${\rho }_i$ 不为 $0$。
  • 构造统计量$$Q=T(T+2)\sum _{k=1}^s\frac{r_k^2}{T-k}\sim {\chi }^2(s-n)$$
  • $T$ 表示样本的个数，$n$ 表示模型中未知参数的个数(ARMA(p,q) n=p+q+1)，$s$ 根据样本量大小进行选取。

7. ARIMA(p,d,q)

• 目的：处理非平稳有 $d$ 阶单位根的数据，进行 $d$ 阶差分。
   
  $y_t^{\prime }={\Delta }^d{y}_t=(1-L{)}^d{y}_t$
  $$y_t^{\prime }={\alpha }_0+\sum _{i=1}^p{\alpha }_i{y}_{t-i}^{\prime }+{ϵ}_t+\sum _{i=1}^q{\beta }_i{ϵ}_{t-i}\rightleftharpoons (1-\sum _{i=1}^p{L}^i{\alpha }_i)(1-L{)}^d{y}_t={\alpha }_0+(1+\sum _{i=1}^q{L}^i{\beta }_i){ϵ}_t$$
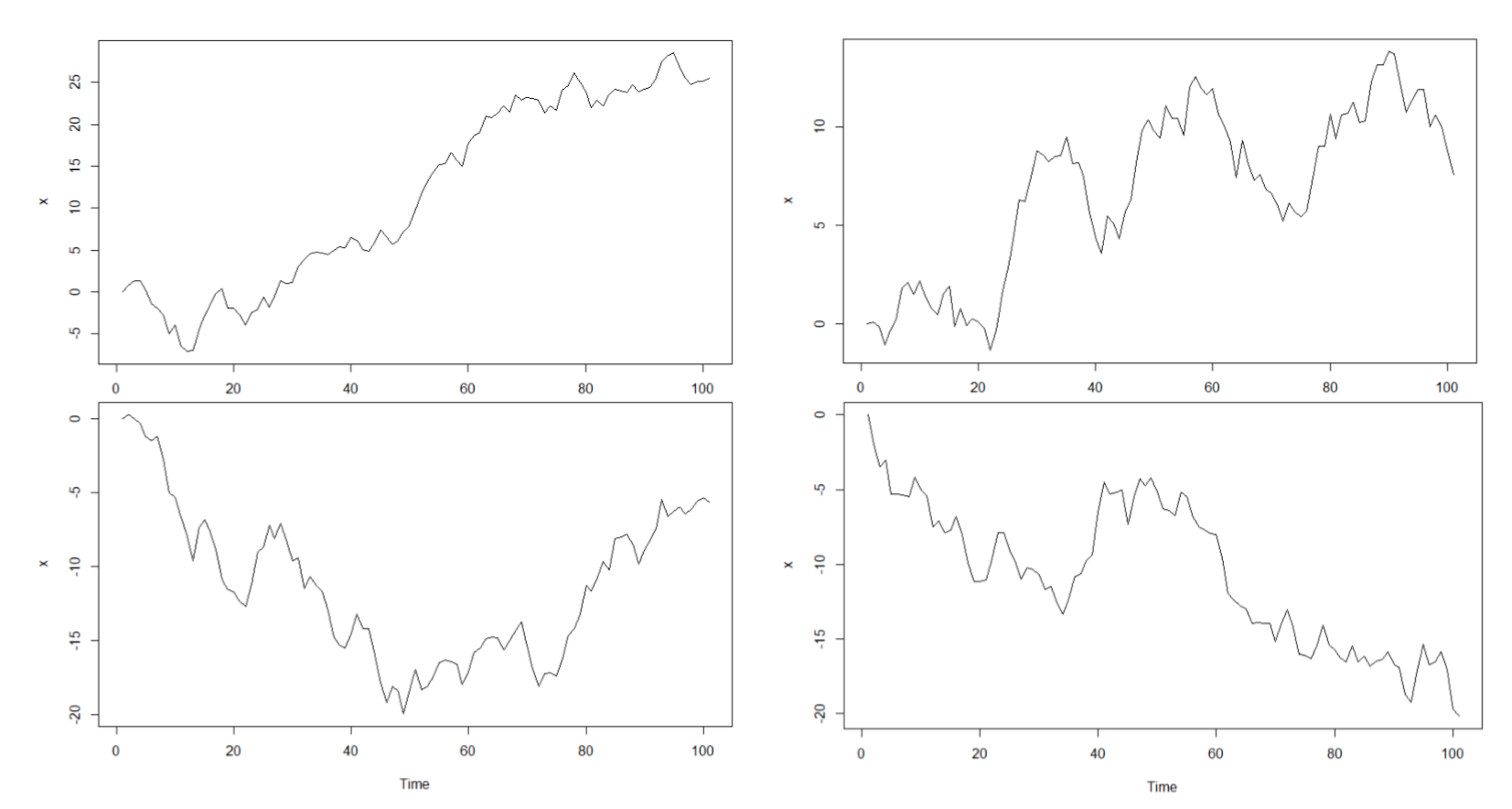
  下面是 ARIMA(1,1,1)的曲线图

8. SARIMA模型

• 目的：增加对季节性因素的考虑。
   
  $SARIMA(p,d,q)(P,D,Q{)}_m$ $m$ 表示周期数。