规划类模型

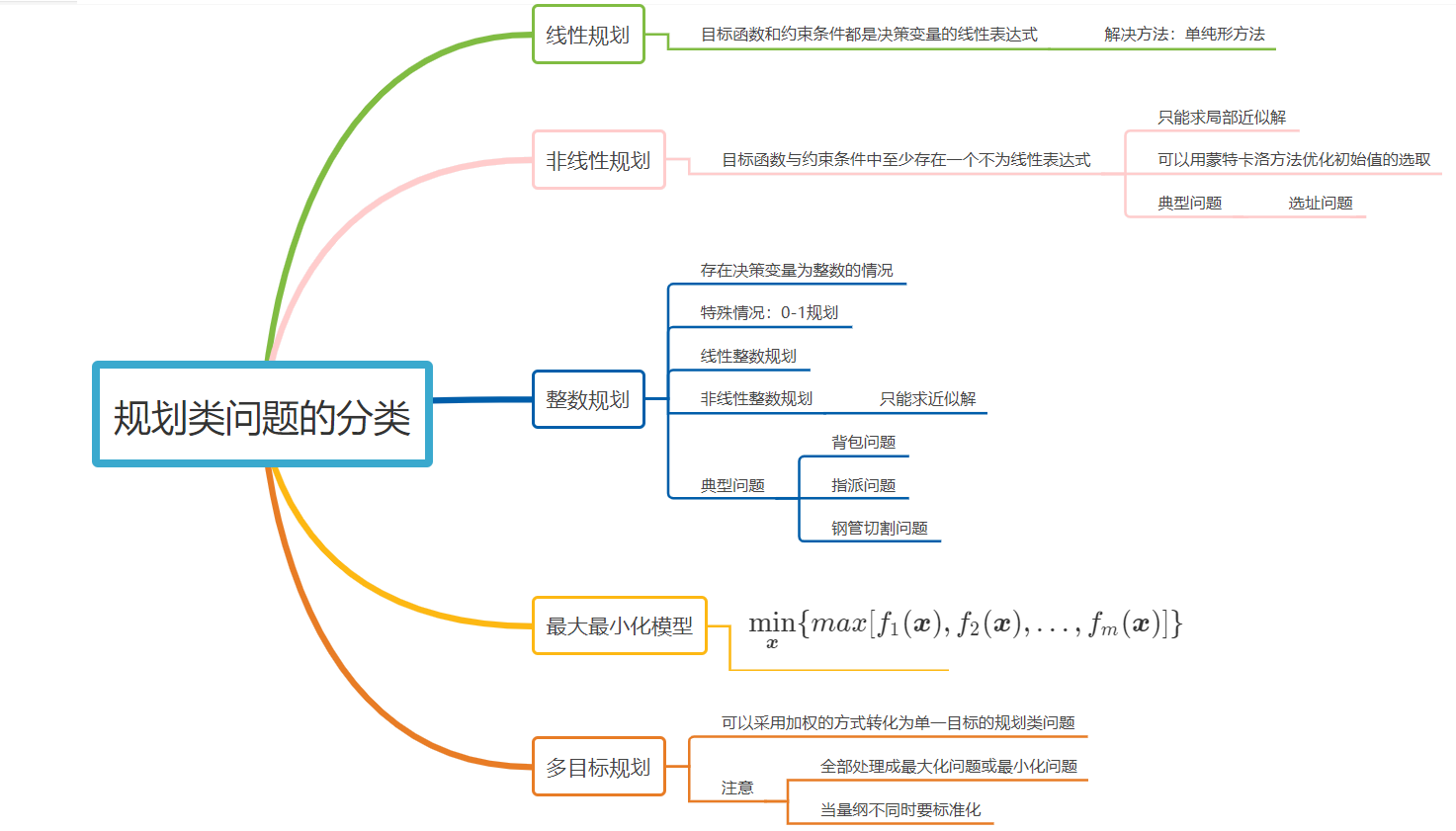
文章目录

(1) 线性规划
(2) 非线性规划
(3) 整数规划
- 1. matlab求解整数规划的函数
- 2. matlab求解 0-1 规划的函数
(4) 最大最小化模型
- 1. matlab 中最大最小化模型的标准形式
- 2. matlab求解最大最小化模型的函数
(5) 多目标规划模型

(1) 线性规划

1. matlab 中线性规划的标准型

$目标函数：\min f(\boldsymbol{x})=C^TX$
$C=\left[ \begin{matrix} c_1\\ c_2\\ \vdots\\ c_n \end{matrix} \right]~~~ X=\left[ \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right]$
$约束条件：s.t.\left\{ \begin{aligned} &AX\le \boldsymbol{b} ~~①\\ &Aeq\cdot X=beq~~②\\ & \boldsymbol{lb}\le X\le \boldsymbol{ub}~~③ \end{aligned} \right.$
包含不等式约束 $①$ ，等式约束 $②$ ，上下界约束 $③$ 。

2. matlab求解线性规划的函数

[x,fval]=linprog(C,A,b,Aeq,beq,lb,ub,x0)

除 x0 表示初始值一般不用给出，其余均为标准型中的表示。
当不存在等式或者不等式约束时可以使用 [] 来代替。
当某个变量 xi 没有上下界约束时可以使用 -inf 和 inf 来表
示。
返回的 x 表示在最小值处的 x 的取值，fval 表示取得的最小值。
与标准形式不同的处理方法：
- 如果需要求最大值，则可以添加负号转为求解最小值，一定注意求解完后要的真实解是 -fval。
- 如果不等式约束中存在 $\ge$ 号则可以通过两边同乘负号转化为 $\le$ 。
- 如果存在的是 $<$ ，则可以取一个稍微大一点的数字将 $<$ 转化成 $\le$ 。

3. matlab程序的一个例子

$目标函数：\max z=20x_1+10x_2+5x_3$
$约束条件：s.t.\left\{ \begin{aligned} &5x_1+4x_2+2x_3\le 24\\ &2x_1+5x_2\ge 13\\ &3x_2+x_3=12\\ & x_1 \ge 0\\ \end{aligned} \right.$

C=[-20,-10,-5]';
A=[5,4,2;-2,-5,0];
b=[24,-13]';
Aeq=[0,3,1]';
beq=[12];
lb=[0,-inf]';
ub=[+inf,+inf];
[x,fval]=linprog(C,A,b,Aeq,beq,lb,ub,x0);
fval=-fval; %由于是求最大值，因此要求结果的相反数。

(2) 非线性规划

1. matlab 中非线性规划的标准型

$目标函数：\min f(\boldsymbol{x})$

$约束条件：s.t.\left\{ \begin{aligned} &AX\le \boldsymbol{b} ~~①\\ &Aeq\cdot X=beq~~②\\ & \boldsymbol{lb}\le X \le \boldsymbol{ub}~~③\\ & c(\boldsymbol{x})\le 0~~④\\ & ceq(\boldsymbol{x})=0~~⑤\\ \end{aligned} \right.$
包含不等式约束 $①$ ，等式约束 $②$ ，上下界约束 $③$ ，非线性约束 $④$ ，非线性等式 $⑤$ 。

2. matlab求解非线性规划的函数

[x,fval]=fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)

x0 表示初始值，由于非线性规划只能求解局部最优，因此 x0 的选择十分重要。
如果要求解全局最优解，可以先使用蒙特卡洛给出一个模拟的最优解的 x0，之后再将这个 x0 当做初始值使用函数求解。
option 提供求解方法的选择: interior-point （内点法，默认）、sqp（序列二次规划法）、active-set（有效集法）、trust-region-reflective（信赖域反射算法）。

3. fun 函数

@fun 中的 fun 表示要编写一个独立的 “.m” 文件存储目标函数，x 表示决策变量的向量。

function f=fun(x)
    f=...
end

4. nonlfun 函数

@nonlfun 中的 nonlfun 表示要编写一个独立的 “.m” 文件存储目非线性约束条件。

function [C,ceq]=nonlfun(x)
    c=[非线性不等式约束1;
      ...
      非线性不等式约束k];
    ceq=[非线性等式约束1
    ...
      非线性等式约束 s];
end

注意要写成 matlab 可以识别的形式，例如 $f(\boldsymbol{x})=3x_1^2+4x_2+x_3^3$ 需要写成 f=3*x(1)^2+4*x(2)+x(3)^3。

5. matlab程序的一个例子

$目标函数：\min z=x_1^2+x_2^2+x_3^2+8$
$约束条件：s.t.\left\{ \begin{aligned} &x_1^2+4x_2^2+x_3^2\le 24\\ &x_1^2+5x_2\ge 13\\ &-x_2^2+x_3^2=12\\ & x_1,x_2,x_3 \ge 0\\ \end{aligned} \right.$

main.m

A=[];
b=[];
Aeq=[];
beq=[];
lb=[0,0,0]';
ub=[+inf,+inf];
x0=[0,0,0]';
[x,fval]=fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun);

fun.m

function f=fun(x)
    f=x(1)^2+x(2)^2+x(3)^2+8
end

nonlfun.m

function [C,ceq]=nonlfun(x)
    c=[x(1)^2+4*x(2)^2+x(3)^2-24;-x(1)^2-5*x(2)+13];
    ceq=[-x(2)^2+x(3)^2-12];
end

(3) 整数规划

1. matlab求解整数规划的函数

[x,fval]=intlinprog(C,intcon,A,b,Aeq,beq,lb,ub)

不需要给出初始值。
intcon：用来指定哪些变量是整数。
- 例如决策变量有 $x_1,x_2,x_3,x_4$ ，若 $x_1,x_3$ 是整数，则 incton=[1,3]。

2. matlab求解 0-1 规划的函数

只需要在 lb,ub 上进行限制即可。
- 例如决策变量有 $x_1,x_2,x_3,x_4$ ，若 $x_1,x_3$ 是 $0 - 1$ 变量，则 lb=[0,-inf,0,-inf]'，ub=[1,+inf,1,+inf]'。

(4) 最大最小化模型

解决在最不利的条件下寻求最有利的策略，例如选择与医院的距离，要保证离的最远的小区与医院的距离也较小。

1. matlab 中最大最小化模型的标准形式

$目标函数：\min_\boldsymbol{x} \{max[f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\dots,f_m(\boldsymbol{x})]\}$

2. matlab求解最大最小化模型的函数

[x,fval]=fminimax(@Fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)

目标函数 Fun 使用一个函数向量表示。

function f=Fun(x)
  f=zeros(m,1);
  f(1)=...
  ...
  f(m)=...
end

(5) 多目标规划模型

当一个优化问题存在多个优化目标函数时，可以通过加权的方式将这几个优化目标函数组合起来。

⚠️注意

加权时要将每个目标函数都统一成最大化或者最小化问题。
如果量纲不同，应当先进行标准化处理。

详细解析规划类模型（matlab）