聚类分析
这里主要要注意的地方就是聚类与分类之间的区别:分类面向的是已知的类别,大部分情况是通过对已有的数据进行学习,之后再对新来的一个数据进行类别的预测,而聚类面向的是未知的类别,是按照“距离”对已知数据直接分类。
文章目录
(1) K-means聚类
1. 流程
step 1: 选定要划分的类的个数 k k k 。
step 2: 随机选取 k k k 个起始的中心点(不一定要是样本中的点) 。

step 3: 进行迭代,每次迭代都重新选择样本的中心,一直迭代到样本的中心不再移动,或者到达指定的迭代次数。
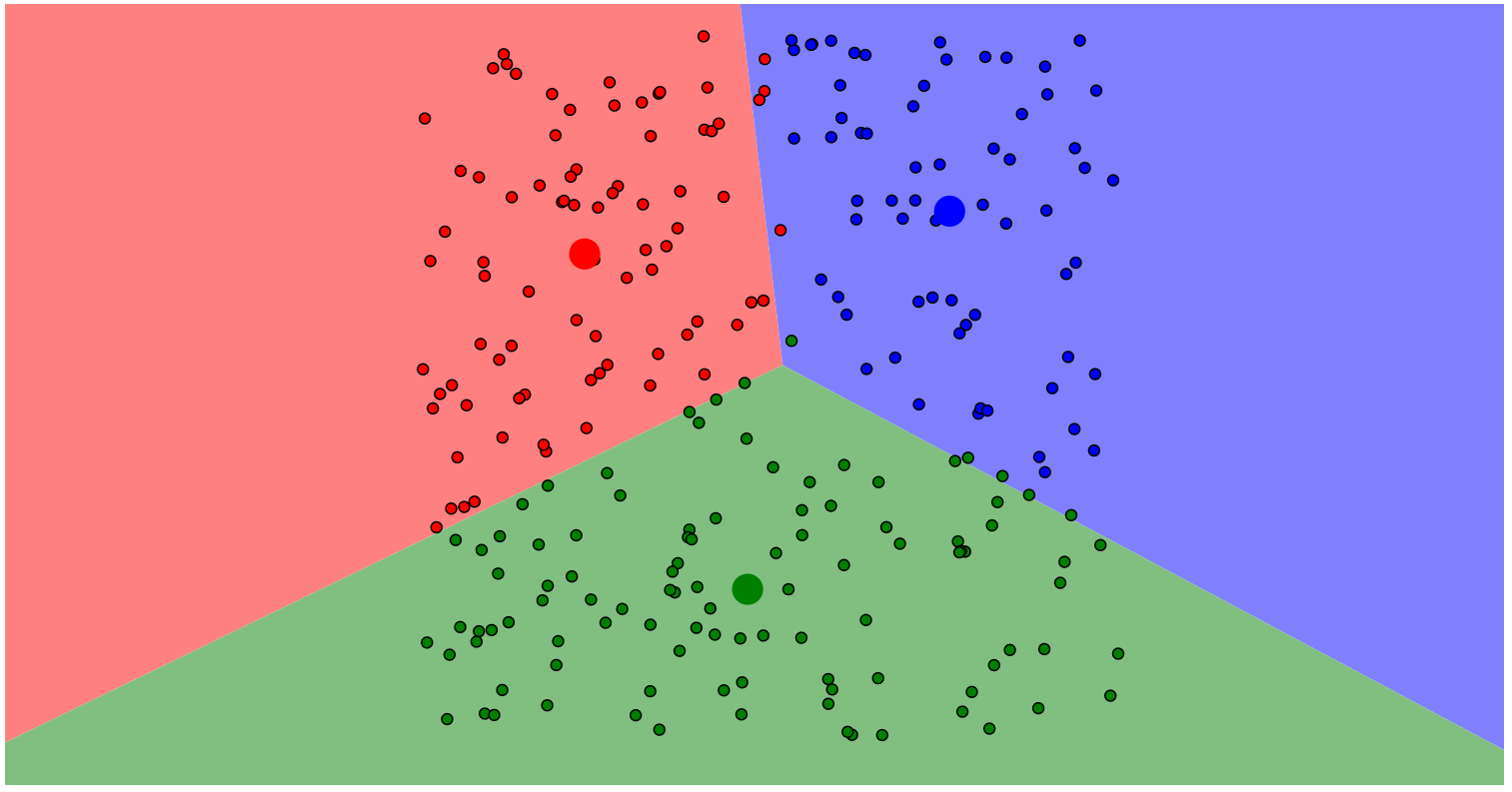
2. 优缺点分析
- 优点:
- 算法简单,快捷。
- 处理大数据集的效率较高。
- 缺点
- 必须先确定要生成的类别的数量。
- 对选择的初值较为敏感。
- 容易被噪声干扰。
3. 改进方法 Kmeans++
- 可以解决 Kmeans 的第二和第三个问题。
- 改进体现在 k 个初值的选取上。
- 流程:
- 随机选取一个样本作为第一个聚类中心。
- 计算每个样本点到所有的聚类中心的距离,并且按照距离远近进行概率的设定,距离越远,概率越大。
- 按照轮盘法(按照选取概率的大小进行抽取)的规则进行下一个聚类中心的选择,直到完成 k 个聚类中心的选择。
4. 归一化处理
当数据的量纲不一致时,要进行归一化处理,对于样本的同一个特征构造一个新的量。
z i = x i − x ‾ σ x z_i=\dfrac{x_i-\overline{x}}{\sigma_x} zi=σxxi−x
(2) 系统(层次)聚类
1. 样本与样本之间的常用距离
定义 x i ⃗ = ( x i 1 , x i 2 , … , x i p ) ′ \vec{x_i}=(x_{i1},x_{i2},\dots,x_{ip})' xi=(xi1,xi2,…,xip)′, x j ⃗ = ( x j 1 , x j 2 , … , x j p ) ′ \vec{x_j}=(x_{j1},x_{j2},\dots,x_{jp})' xj=(xj1,xj2,…,xjp)′。
- 绝对值距离: d ( x i ⃗ , x j ⃗ ) = ∑ k = 1 p ∣ x i k − x j k ∣ d(\vec{x_i},\vec{x_j})=\displaystyle\sum_{k=1}^{p}|x_{ik}-x_{jk}| d(xi,xj)=k=1∑p∣xik−xjk∣。
- 欧氏距离: d ( x i ⃗ , x j ⃗ ) = ∑ k = 1 p ( x i k − x j k ) 2 d(\vec{x_i},\vec{x_j})=\displaystyle\sum_{k=1}^{p}\sqrt{(x_{ik}-x_{jk})^2} d(xi,xj)=k=1∑p(xik−xjk)2。
- 明可夫斯基距离: d ( x i ⃗ , x j ⃗ ) = ∑ k = 1 p [ ( x i k − x j k ) q ] 1 q d(\vec{x_i},\vec{x_j})=\displaystyle\sum_{k=1}^{p}[(x_{ik}-x_{jk})^q ]^{\frac{1}{q}} d(xi,xj)=k=1∑p[(xik−xjk)q]q1
- 切比雪夫距离: d ( x i ⃗ , x j ⃗ ) = max 1 ≤ k ≤ p ∣ x i k − y j k ∣ d(\vec{x_i},\vec{x_j})=\max\limits_{1\le k\le p}|x_{ik}-y_{jk}| d(xi,xj)=1≤k≤pmax∣xik−yjk∣
- 马氏距离: d ( x i ⃗ , x j ⃗ ) = ( x i ⃗ − x j ⃗ ) ′ ∑ − 1 ( x i ⃗ − x j ⃗ ) 。 d(\vec{x_i},\vec{x_j})= (\vec{x_i}-\vec{x_j})'\sum^{-1}(\vec{x_i}-\vec{x_j})。 d(xi,xj)=(xi−xj)′∑−1(xi−xj)。 其中 ∑ \sum ∑ 为样本的协方差矩阵。
2. 类与类之间的常用距离
① ① ① 单独一个样本组成的类,类之间的距离与样本之间的距离相同。
② ② ② 多个样本组成的类:
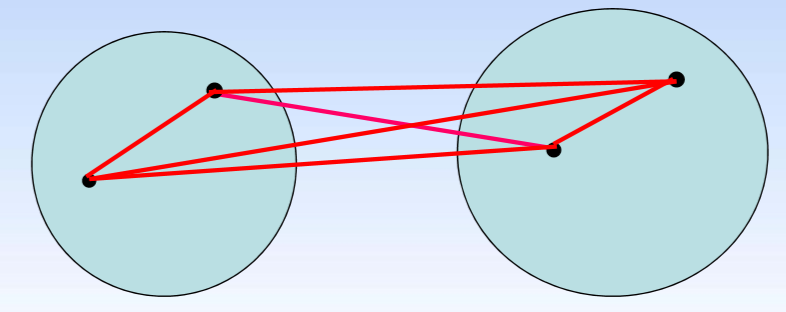
定义的说明: G p G_p Gp, G q G_q Gq 是两个类, D ( G p , G q ) D(G_p,G_q) D(Gp,Gq) 表示两个类之间的距离。 ∀ x i ⃗ ∈ G p \forall\vec{x_i}\in G_p ∀xi∈Gp, ∀ x j ⃗ ∈ G q \forall\vec{x_j}\in G_q ∀xj∈Gq, d ( x i ⃗ , x j ⃗ ) d(\vec{x_i},\vec{x_j}) d(xi,xj) 表示这两个点之间的距离。
- 最短距离法: D ( G p , G q ) = m i n D(G_p,G_q)=min D(Gp,Gq)=min d ( x i ⃗ , x j ⃗ ) d(\vec{x_i},\vec{x_j}) d(xi,xj)
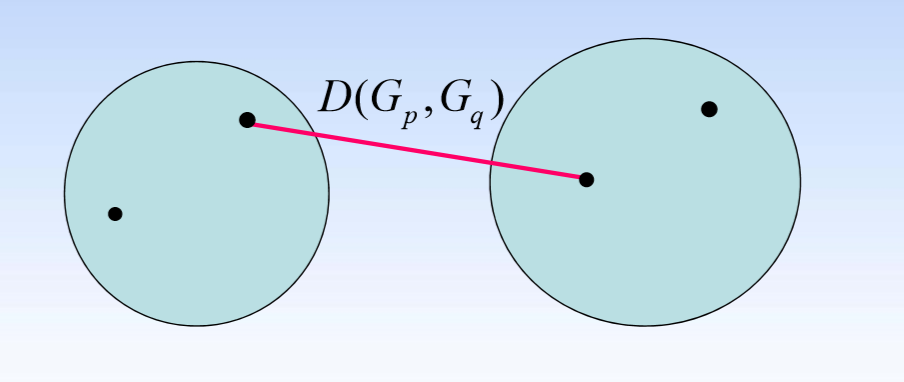
- 最长距离法: D ( G p , G q ) = m a x D(G_p,G_q)=max D(Gp,Gq)=max d ( x i ⃗ , x j ⃗ ) d(\vec{x_i},\vec{x_j}) d(xi,xj)
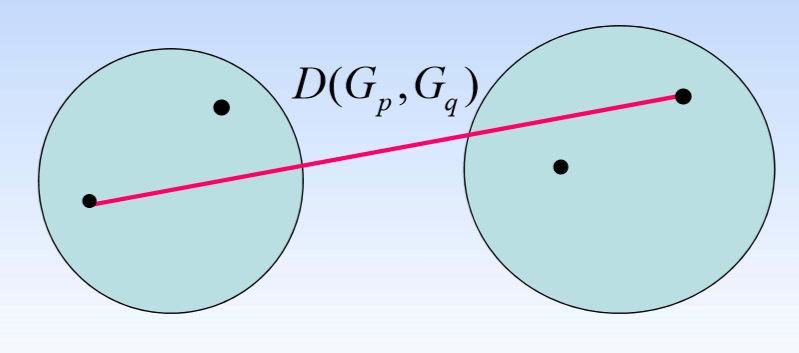
- 组间平均连接法: D ( G p , G q ) = d 1 + d 2 + d 3 + d 4 4 D(G_p,G_q)=\dfrac{d_1+d_2+d_3+d_4}{4} D(Gp,Gq)=4d1+d2+d3+d4
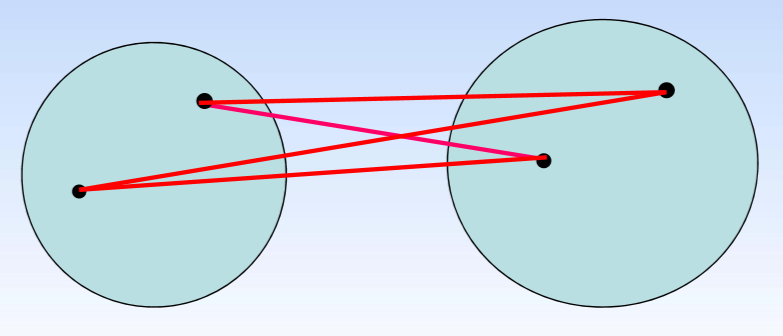
- 组内平均连接法: D ( G p , G q ) = d 1 + d 2 + d 3 + d 4 + d 5 + d 6 6 D(G_p,G_q)=\dfrac{d_1+d_2+d_3+d_4+d_5+d_6}{6} D(Gp,Gq)=6d1+d2+d3+d4+d5+d6
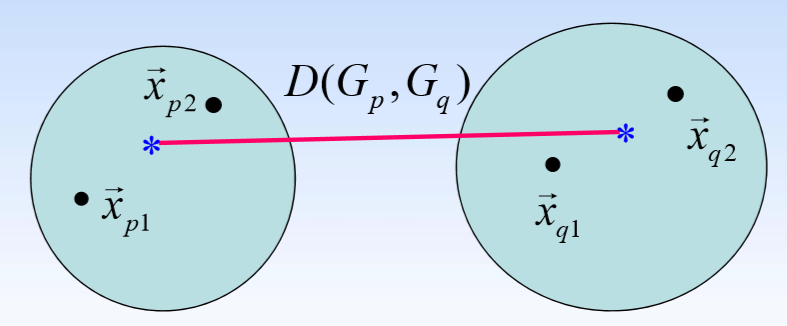
- 重心法: D ( G p , G q ) = d ( x ‾ p , x ‾ q ) D(G_p,G_q)=d(\overline{x}_p,\overline{x}_q) D(Gp,Gq)=d(xp,xq)
对两个类进行如下定义:
x ‾ p = x ⃗ p 1 + x ⃗ p 2 2 \overline{x}_p=\dfrac{\vec x_{p1}+\vec x_{p2}}{2} xp=2xp1+xp2
x ‾ q = x ⃗ q 1 + x ⃗ q 2 2 \overline{x}_q=\dfrac{\vec x_{q1}+\vec x_{q2}}{2} xq=2xq1+xq2
3. 系统聚类的流程
step 1: 计算 n n n 个样本两两之间的距离 d i j d_{ij} dij 。
step 2: 构造 n n n 个类,每个类只含一个样本。
step 3: 进行迭代,每次迭代都合并最近的两个类为一个新类,并计算新类与当前各类之间的距离。
step 4: 当类的个数 = 1 =1 =1 后结束迭代,并做出聚类的谱系图。

4. 用图形估计聚类的数量
- 肘部法则:通过图形大致的估计出最优的聚类数量。
- 各个类畸变程度之和:各个类的畸变程度等于该类重心与其内部成员位置距离的平方和。
- 假设 n n n 个样本被划分到 K K K ( K ≤ n − 1 ) (K\le n-1) (K≤n−1) 个类中,用 C k C_k Ck 表示第 k k k ( k = 1 , 2 , … , K ) (k=1,2,\dots,K) (k=1,2,…,K)个类,且该类重心记为 u k u_k uk,则第 k k k 个类的畸变程度为 ∑ i ∈ C k ∣ x i − u k ∣ 2 \sum_{i\in C_k}|x_i-u_k|^2 ∑i∈Ck∣xi−uk∣2。
- 所有类的总畸变程度(聚合系数)为: J = ∑ k = 1 K ∑ i ∈ C k ∣ x i − u k ∣ 2 J=\sum_{k=1}^{K}\sum_{i\in C_k}|x_i-u_k|^2 J=k=1∑Ki∈Ck∑∣xi−uk∣2
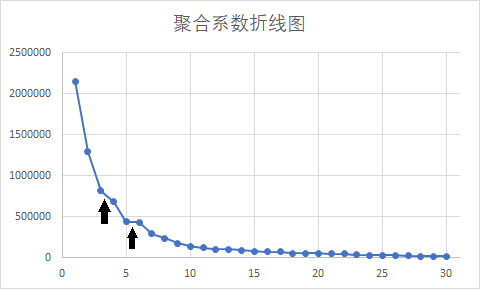
- 聚合系数折线图:横坐标为聚类的类别数 K K K ,纵坐标为聚合系数 J J J。一般选取达到平稳之前的一个值作为聚类的类别数 K K K。
(3) DBSCAN聚类
1. 基本概念
- 数据点的三个分类:
- 核心点:在半径 Eps 内含有不少于 MinPts 数目的点。
- 边界点:在半径 Eps 内点的数量小于 Minpts,但是落在核心点的邻域内。
- 噪音点:既不是核心点也不是边界上的点。

2. 优缺点与适用性
- 优点:
- 能处理任意形状与大小的类。
- 不用确定 K K K 的大小。
- 可以在聚类的过程中发现噪声点。
- 缺点:
- ε ε ε 和 minPts 不好确定。
- 计算效率较低,数据量较大时不易处理。
一般在二维情况下,做出散点图之后看是否合适使用 DBSCAN。
下面上一张 DBSCAN 笑脸:
