模糊评价

模糊评价
在对指标进行评价时与 TOPSIS 类似

(1) 模糊数学的简介

1. 模糊数学的归类

2. 模糊集合与隶属函数

• 模糊集合：用来描述模糊性概念的集合，例如高、富、帅等，与经典集合相比，模糊集合承认亦此亦彼，元素可以既属于 $A$，也属于 $\overline{A}$。
• 数学中对模糊集合的刻画：隶属函数

  • 定义模糊集合 $A$，例如 $A=$ 长得高。

  • 定义论域，例如身高的集合 $\mho =[150cm,220cm]$。

  • 对于 $\mho$ 中的每一个元素，均对应于 $A$ 的一个隶属度，隶属度介于 $[0,1]$ 。

  • 下面定义了一个隶属函数 $u_A：\mho \to [0,1]$
    $$u_A(x)=\{\begin{array}{rlr}& 0& 150\le x\le 170\\ & \frac{x-170}{20}& 170\le x\le 190\\ & 1& 190\le x\le 220\end{array}$$

    

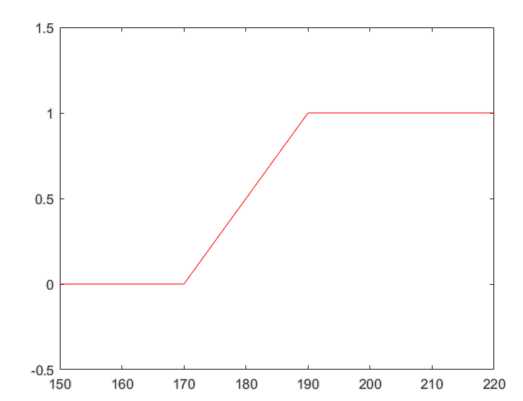
  • 身高集合中的每一个元素均可以通过隶属函数对应到 $A$ 的一个隶属度，隶属度越大表示越属于集合 $A$ 中的特性，注意隶属函数的选取是任意的。

3. 模糊集合的表示

定义论域为 ℧ = { x 1 , x 2 , … , x n } \mho=\{x_1,x_2,\dots,x_n\} ℧={ x1​,x2​,…,xn​}，定义模糊集合为 $A$，定义隶属度为 $A(x_i)(i=1,2,\dots ,n)$

• 表示方法：
  zadeh 表示方法 $A=\frac{A(x_1)}{x_1}+\frac{A(x_2)}{x_2}+\cdots +\frac{A(x_n)}{x_n}$
  ⚠️ 一定注意这只是一种表示方法，并不代表相加的关系，仅仅表示 $A$ 是由这些元素组成的。

4. 模糊集合的分类

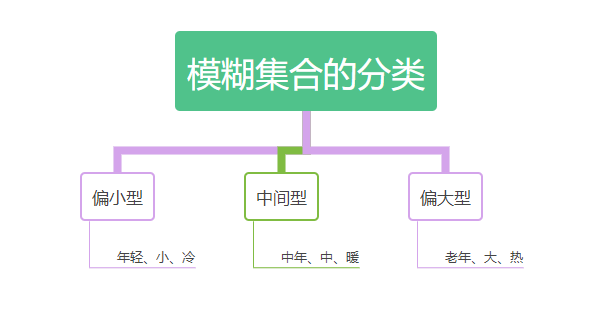
可以想象相关的函数图形大致的趋势。

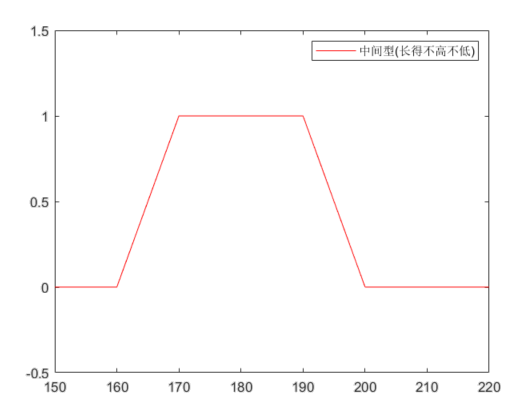
(2) 隶属度的确定方法

1. 模糊统计法

• 找多个人对一个局部的概念进行描述，用隶属频率定义隶属度。

2. 借助已有的客观尺度

• 注意指标必须介于 $[0,1]$，如果不是可以进行归一化处理。
  例如：

  论域	模糊集	隶属度
  设备	设备完好	设备完好率
  产品	质量稳定	正品率
  家庭	小康家庭	恩格尔系数

3. 指派法

• 根据问题的性质直接套用某些分布函数作为隶属函数，注意隶属函数不唯一，合理即可。

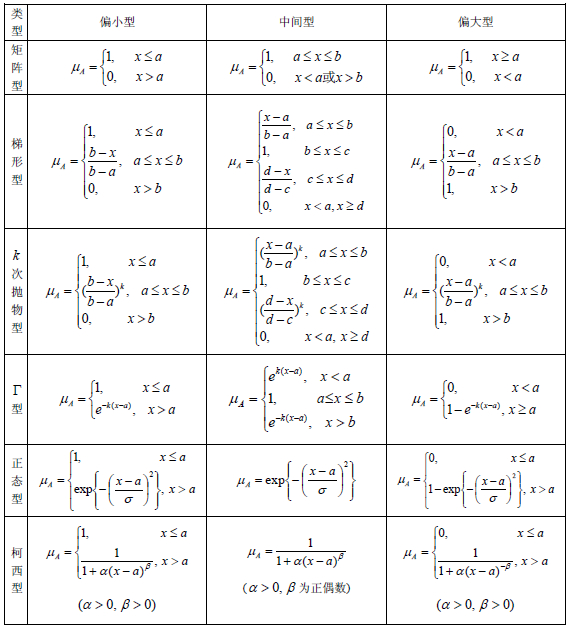
• 对于没有确定参数的分布可以根据生活经验（或者别人的研究结果、常识确定）。

(3) 应用：模糊综合评价

1. 评价问题概述

• 可以解决的问题：
  • 把论域中的对象对应评语集中一个指定的评语。
  • 将方案作为评语集并选择一个最优的方案。
• 模糊综合评价中的集合
  • 因素集 (评价指标集)： U = { u 1 , u 2 , … , u n } U=\{u_1,u_2,\dots,u_n \} U={ u1​,u2​,…,un​}
  • 评语集 (评价的结果)： V = { v 1 , v 2 , … , v m } V=\{v_1,v_2,\dots,v_m\} V={ v1​,v2​,…,vm​}
  • 权重集 (指标的权重)： A = { a 1 , a 2 , … , a n } A=\{a_1,a_2,\dots,a_n\} A={ a1​,a2​,…,an​}

⭐️例如在评价一名学生： U = { 专 业 排 名 、 课 外 实 践 、 竞 赛 加 分 、 志 愿 活 动 } V = { 优 、 良 、 差 } A = { 0.5 、 0.1 、 0.3 、 0.1 } \begin{aligned} U&=\{专业排名、课外实践、竞赛加分、志愿活动\}\\ V&=\{优、良、差\}\\ A&=\{0.5、0.1、0.3、0.1\} \end{aligned} UVA​={ 专业排名、课外实践、竞赛加分、志愿活动}={ 优、良、差}={ 0.5、0.1、0.3、0.1}​

2. 一级模糊评价问题

流程

• step 1： 确定因素集。对评价对象的评价需要从多个方面进行综合评判，也就是找出多个评价的角度，例如学生的专业排名、课外实践等。
  U = { u 1 , u 2 , … , u n } U=\{u_1,u_2,\dots,u_n \} U={ u1​,u2​,…,un​}
• step 2： 确定评语集。注意评语集中的元素个数与因素集中的元素的个数没有必然联系。
  V = { v 1 , v 2 , … , v m } V=\{v_1,v_2,\dots,v_m\} V={ v1​,v2​,…,vm​}
• step 3： 确定各因素的权重，为了区别不同的因素在最终评价上起到的重要性不同的作用。
  A = { a 1 , a 2 , … , a n } A=\{a_1,a_2,\dots,a_n\} A={ a1​,a2​,…,an​}
  确定权重的方法：Delphi方法 (专家调查法：征求专家意见)，也可以考虑熵权法和层次分析法，注意应满足 $\sum _{i=1}^n{a}_i=1。$
• step 4： 确定模糊综合判断矩阵
  • 对指标 $u_i$ 的评判记为$$R_i=[r_{i1},r_{i2},r_{i3},\dots ,r_{im}]$$
    其中 $r_{ij}$ 表示评价对象的第 $i(i=1,\dots ,n)$ 个指标对第 $j(j=1,\dots ,n)$ 个评语的隶属度。
  • 模糊综合判断矩阵为：
    $$R=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1m}\\ r_{21}& r_{22}& \cdots & r_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& \cdots & r_{nm}\end{array}\right]$$
• step 5： 综合评价
  $$B_{1\times m}=A_{1\times n}\times R_{n\times m}$$
  $$B=[b_1,b_2,b_3,\dots ,b_m]$$
  其中 $b_i$ 表示评价对象对第 $i$ 个评价量的隶属度，取 $\max b_i$ 对应的评价量为最终的评价量。

分类

• type 1： 把论域中的对象对应评语集中一个指定的评语。
  例如：评价空气质量等级，测得污染物浓度依次为$$(0.07,0.20,0.125,5.00,0.08,0.14)$$ 各污染物权重依次为$$(0.1,0.2,0.3,0.3,0.05,0.05)$$

	1级	2级	3级	4级
$\mathbf{S}{\mathbf{O}}_2$	0.05	0.15	0.25	0.5
$\mathbf{T}\mathbf{S}\mathbf{P}$	0.12	0.30	0.50	1.00
$\mathbf{N}{\mathbf{O}}_{\mathbf{x}}$	0.10	0.10	0.15	0.30
$\mathbf{C}\mathbf{O}$	4.00	4.00	6.00	10.00
$\mathbf{P}{\mathbf{M}}_1$	0.05	0.15	0.25	0.50
${\mathbf{O}}_3$	0.12	0.16	0.20	0.40

• type 2： 将方案作为评语集并选择一个最优的方案。
  例如：选择最佳方案,注意此时与TOPSIS方法相比相当于使用隶属函数进行了一个“正向化”的操作。

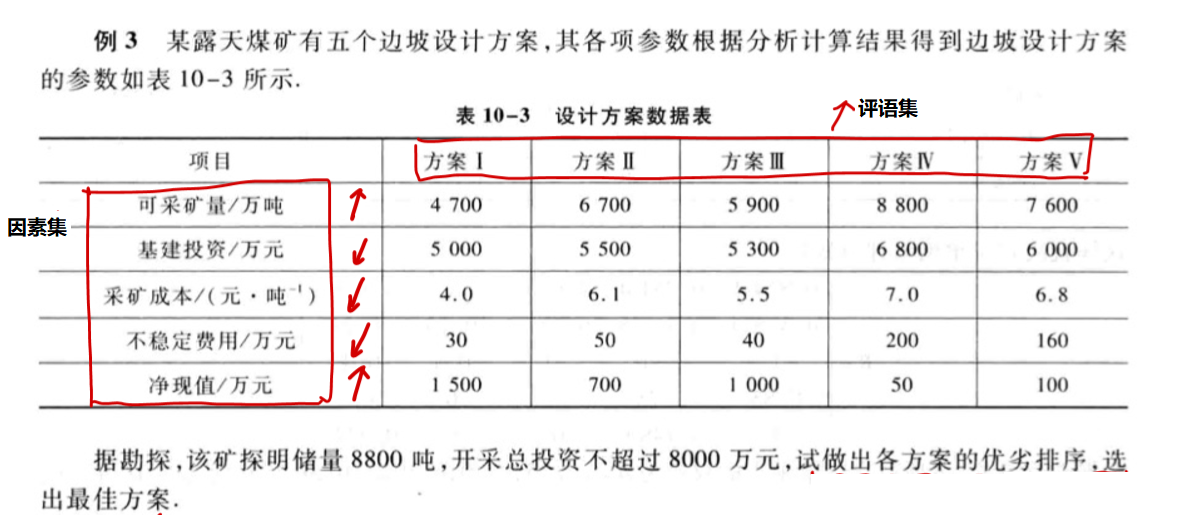
3. 多级模糊评价问题

• 引入多级的原因：当因素类型相似的比较多的情况下，可以进行适当的归类，归类以后方便权重的计算。

流程

• step 1： 划分因素集为若干组 U = { u 1 , u 2 , … , u n } → U = { U 1 , U 2 , … , U k } U=\{u_1,u_2,\dots,u_n\}\rightarrow U=\{U_1,U_2,\dots,U_k\} U={ u1​,u2​,…,un​}→U={ U1​,U2​,…,Uk​}并且保证 $$U=\bigcup _{i=1}^k{U}_i,U_i\bigcap U_j=\varnothing$$
  $$U：第一因素集，U_i：第二因素集$$
• step 2： 确定评语集与权重集 V = { v 1 , v 2 , … , v m } V=\{v_1,v_2,\dots,v_m\} V={ v1​,v2​,…,vm​}
  并对第二因素集 U i = { u 1 ( i ) , u 2 ( i ) , … , u n ( i ) } U_i=\{u_1^{(i)},u_2^{(i)},\dots,u_n^{(i)}\} Ui​={ u1(i)​,u2(i)​,…,un(i)​} A i = { a 1 ( i ) , a 2 ( i ) , … , a n ( i ) } A_i=\{a_1^{(i)},a_2^{(i)},\dots,a_n^{(i)}\} Ai​={ a1(i)​,a2(i)​,…,an(i)​}进行综合评价得到综合评价矩阵
  $$R_i=\left[\begin{array}{cccc}{r}_{11}^{(i)}& r_{12}^{(i)}& \cdots & r_{1m}^{(i)}\\ r_{21}^{(i)}& r_{22}^{(i)}& \cdots & r_{2m}^{(i)}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}^{(i)}& r_{n2}^{(i)}& \cdots & r_{nm}^{(i)}\end{array}\right]$$
  计算出 $B_i=A_i\times R_i(i=1,2,\dots ,k)$
• step 3： 对一级因素 U = { U 1 , U 2 , … , U k } U=\{U_1,U_2,\dots,U_k\} U={ U1​,U2​,…,Uk​}进行综合评价，找到权重矩阵 A = { a 1 , a 2 , … , a n } A=\{a_1,a_2,\dots,a_n\} A={ a1​,a2​,…,an​}
  求得 $$R=\left[\begin{array}{c}{B}_1\\ B_2\\ ⋮\\ B_k\end{array}\right]$$
  综合评价为 $B=A\times R$