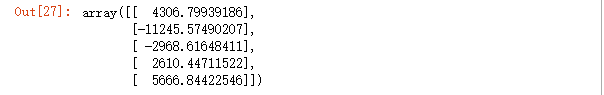基础知识
-
误差ε^(i)是独立并且具有相同的分布,并且服从均值为0方差为θ2的高斯分布
-
独立:张三和李四一起来贷款,他俩没关系
-
同分布:他俩都来得是我们假定的这家银行
-
高斯分布:银行可能会多给,也可能会少给,但是绝大多数情况下这个浮动不会太大,极小情况下浮动会比较大,符合正常情况
高斯分布
蓝点是薪资
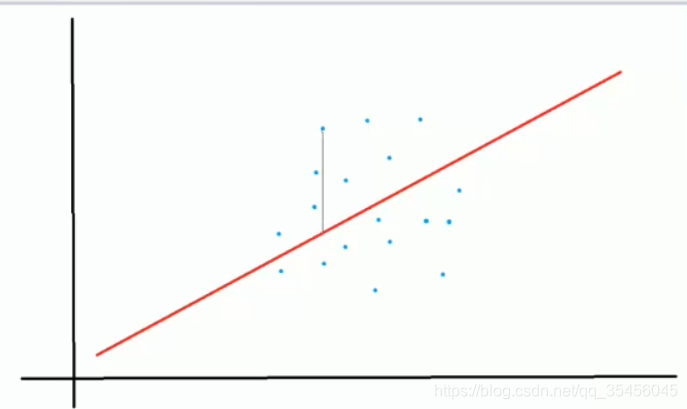
用线连起来,距离越长,误差越大。
误差是服从高斯分布的
预测值与误差:

由于误差服从高斯分布:
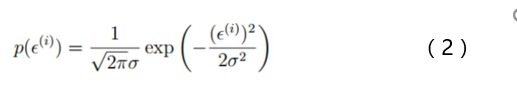
将(1)式带入(2)式得到:
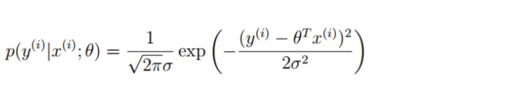
似然函数(累乘):
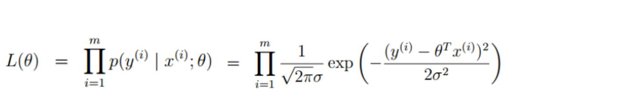
解释:什么样的参数跟我们的数据组合后刚好是真实值
对数似然:
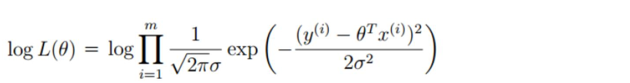
解释:乘法难解,假发就容易了,对数里面乘法可以转换成加法
展开化简:

目标:让似然函数(对数变换后也一样)越大越好
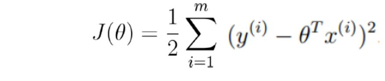
(这就是最小二乘法)
目标函数:
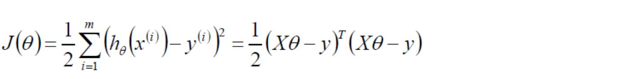
求偏导:
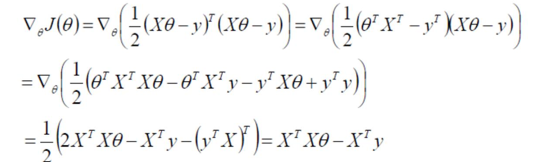
偏导等于0:

代码
未知数是w
y是一个矩阵
x也是一个矩阵
y = wx
想办法让x变成单位矩阵就求出来了w
x如果是长方形矩阵
怎么变成方阵?
先转置

求解w和b
import numpy as np
X = np.array([[4000,25],
[8000,30]])
y = np.array([[20000],
[70000]])
from sklearn.linear_model import LinearRegression
#fit_intercept 需不需要截距=偏置项=误差
lrg = LinearRegression(fit_intercept=False).fit(X,y)
#获取 系数 和 误差
lrg.coef_,lrg.intercept_

#检验
np.dot(X, lrg.coef_.T)

#换成5个样本,验算一下
NX = np.array([[4000,25],
[8000,30],
[5000,28],
[7500,33],
[12000,40]])
np.dot(NX, lrg.coef_.T)#最后三个有很大的误差

3个样本
X = np.array([[4000,25],
[8000,30],
[5000,28]])
y = np.array([[20000],
[70000],
[35000]])
#fit_intercept 需不需要截距=偏置项=误差
lrg = LinearRegression(fit_intercept=False).fit(X,y)
#获取 系数 和 误差
lrg.coef_,lrg.intercept_

np.dot(X,lrg.coef_.T)

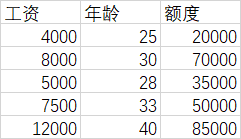
5个样本
X = np.array([[4000,25],
[8000,30],
[5000,28],
[7500,33],
[12000,40]])
y = np.array([[20000],
[70000],
[35000],
[50000],
[85000]])
#fit_intercept 需不需要截距=偏置项=误差
lrg = LinearRegression(fit_intercept=False).fit(X,y)
#获取 系数 和 误差
lrg.coef_,lrg.intercept_
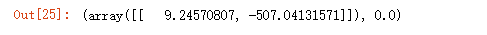
#loss
res = np.dot(X,lrg.coef_.T)
res
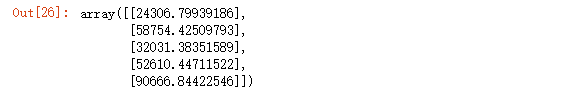
res - y