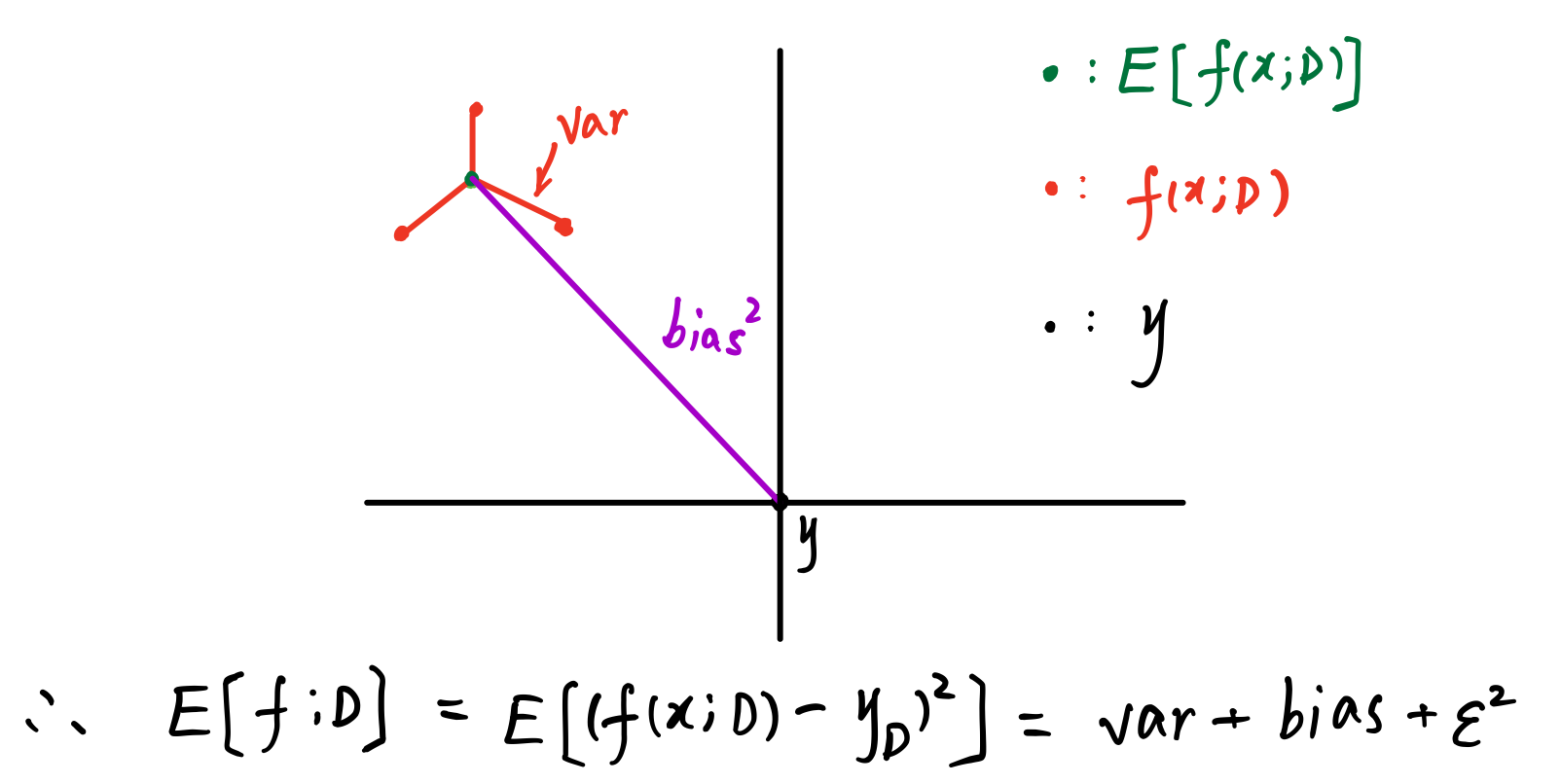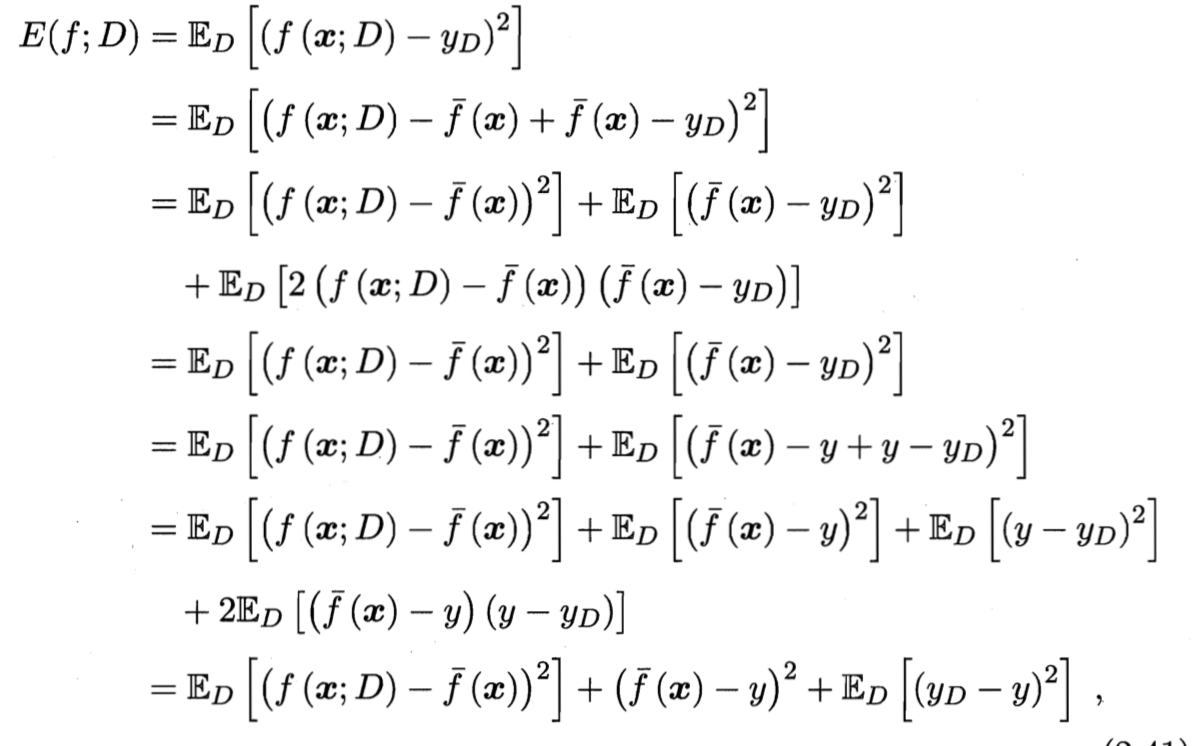偏差-方差分解bias-variance decomposition

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/sunlanchang/article/details/89467966

方差、偏差的直观意义

方差维基百科定义：
$\operatorname{Var}(X)=\mathrm{E}\left[(X-\mu)^{2}\right] 其中\mu=\mathrm{E}(X)$
在给定数据集中
方差：
$\operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\overline{f}(\boldsymbol{x}))^{2}\right]$
偏差：
$\operatorname{bias}^{2}(\boldsymbol{x})=(\overline{f}(\boldsymbol{x})-y)^{2}$
噪声：
$\varepsilon^{2}=\mathbb{E}_{D}\left[\left(y_{D}-y\right)^{2}\right]$
对于方差偏差的解释如下图打靶子所示，红点为打的靶点即预测值，中心靶心为真实值，方差为预测期望值与预测值之间的均方误差如红线所示，偏差是预测期望与真实值的均方误差，总体的函数误差为方差+偏差+数据噪声（数据噪声为标注错误等造成的原始数据不准确）

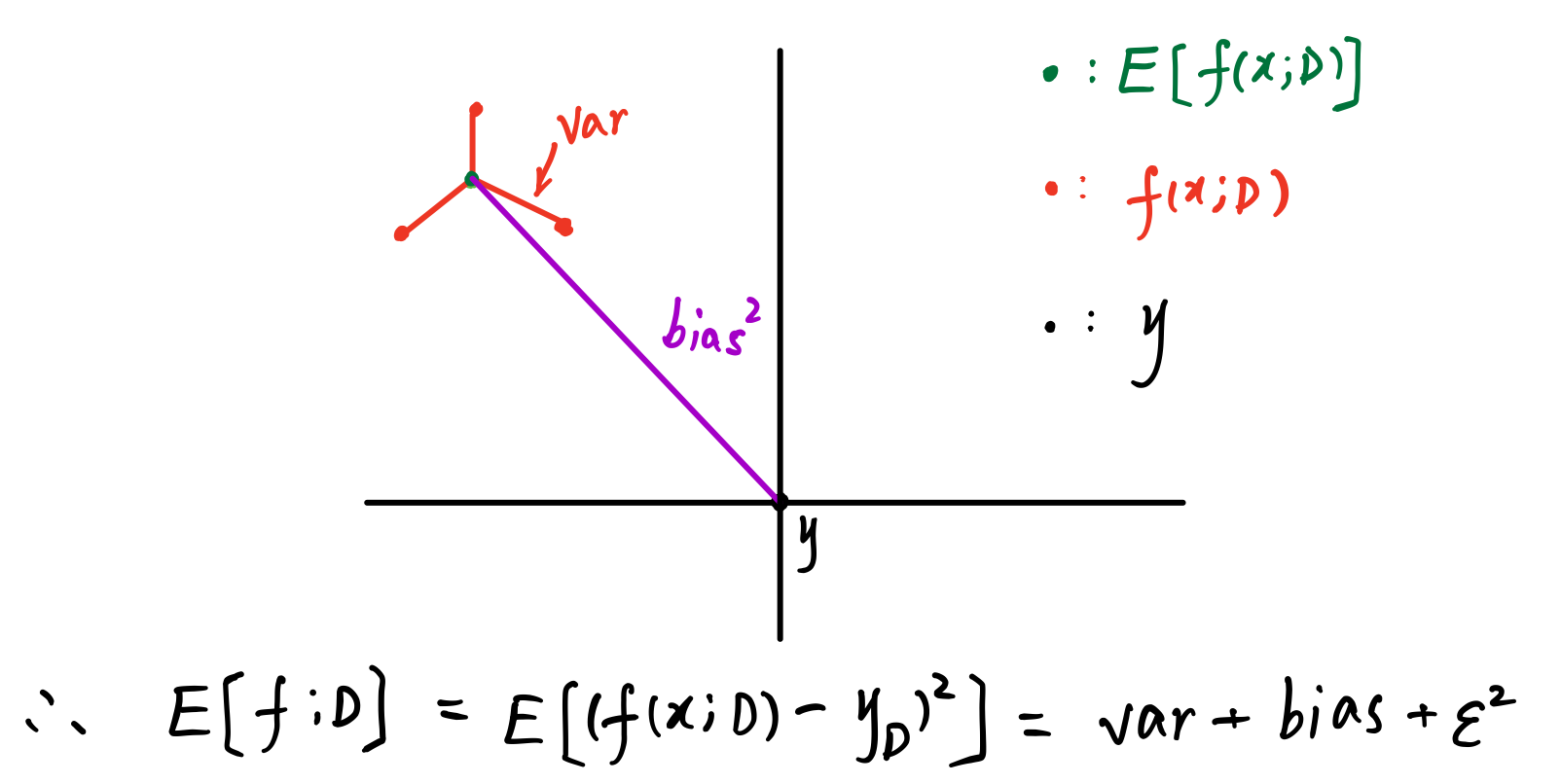
方差-偏差分解

此处的分解只适用于回归问题，对于分类问题得不到这个分解，因为分类问题误差不能基于均方误差。

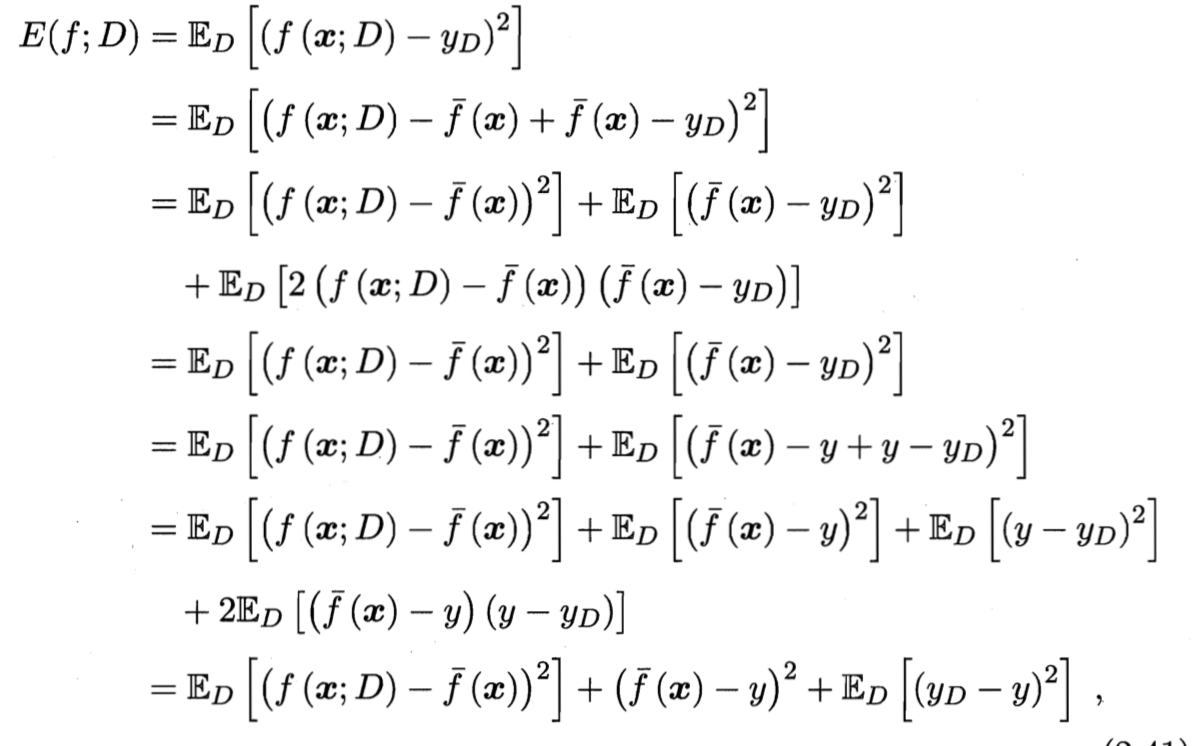
上面等式中第四行等于0的原因是：
$\mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\overline{f}(\boldsymbol{x}))\left(\overline{f}(\boldsymbol{x})-y_{D}\right)\right]=\mathbb{E}_{D}\left(\overline{f}(\boldsymbol{x})-y_{D}\right)\mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\overline{f}(\boldsymbol{x})\right]$
其中 $\mathbb{E}_{D}\left(\overline{f}(\boldsymbol{x})-y_{D}\right)=0$，所以第四行等式等于0。

意义

偏差和方差有冲突，对应着训练模型的欠拟合和过拟合，在训练前期模型欠拟合，模型的误差由偏差主导即期望预测与真实标签差距很远如上图紫色线条所示，训练后期偏差减小，完美的拟合训练数据，对于数据扰动能力减弱，给予新的数据后由于泛化性能减弱造成方差增大。